当前位置:网站首页>BUAA calculator (expression calculation - expression tree implementation)
BUAA calculator (expression calculation - expression tree implementation)
2022-07-06 03:30:00 【star-399】
【 Problem description 】
Read an integer arithmetic expression from standard input , Such as 24 / ( 1 + 2 + 36 / 6 / 2 - 2) * ( 12 / 2 / 2 )= , Evaluate expression results , And the output .
requirement :
1、 Expression operators only have +、-、*、/, At the end of the expression = Character indicates the end of expression input , Spaces may appear in expressions ;
2、 Parentheses appear in the expression , Parentheses may be nested , There will be no wrong expression ;
3、 Division sign appears / when , Divide by integers , The result is still an integer , for example :5/3 The result should be 1.
4、 Expression tree is required to realize expression calculation .
Expression tree (expression tree):
We have known that we use suffix expression and stack to calculate the value of infix expression in computer . In the computer, there is another way to calculate the value of the expression by using the expression tree . An expression tree is such a tree , Its root node is the operator , Non root nodes are operands , Post order traversal of it will calculate the value of the expression . The method of generating expression tree from suffix expression is as follows :
l Read in a symbol :
l If it's an operand , Then create a single node tree and push the pointer to it onto the stack ;
l If it's an operator , Just pop up from the stack and point to two trees T1 and T2 The pointer to (T1 First pop up ) And form a new tree , The root of the tree is the operator , Its left 、 The right subtree points to T2 and T1, Then press the pointer of the new tree onto the stack .
For example, the input suffix is expressed as :
ab+cde+**
Then the generated expression tree is :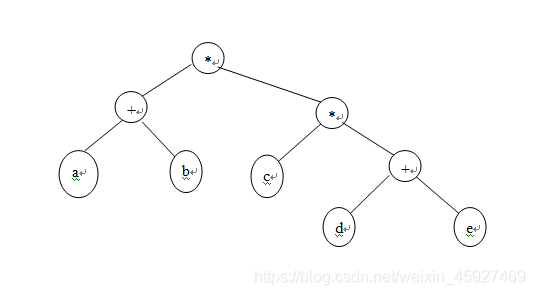
【 Input form 】
Enter a from the keyboard with = Integer arithmetic operation expression at the end . Operators and operands can be separated by spaces .
【 Output form 】
First, output the expression tree root on the screen 、 Operators or operands on the left and right child nodes , Separated by a space in the middle , Finally, there is a carriage return ( If there is no node , This item will not output ). Then output the expression calculation result .
【 The sample input 】
24 / ( 1 + 2 + 36 / 6 / 2 - 2) * ( 12 / 2 / 2 ) =
【 Sample output 】
*/ /
18
【 Sample explanation 】
Calculate the value of the expression according to the operator and bracket priority . In the generated expression tree ,* Is the operator of the root node ,/ Is the operator on the left child node of the root node ,/ Is the operator on the right child node of the root node , Output according to the requirements of the topic .
#include <ctype.h>
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
struct numop
{
// define elemnet
int num;
char op;
} sto[501];
struct opstack
{
// define stack
int top;
struct numop sto[500];
};
struct Tree
{
// define Tree
int n;
char o;
struct Tree *l;
struct Tree *r;
};
struct tree_pro
{
// tree stack
struct Tree tree[502];
int top;
} t;
typedef struct opstack stack;
stack o; // operation
struct Tree *u, *v, *w; // temporary struct
char c;
int i, j, k, n;
void initstack(stack *s)
{
// init stack
s->top = -1;
}
void push_tree(struct tree_pro *t, int m,
char c)
{
// stack in member and operation
if (m != -1)
{
t->tree[++t->top].l = NULL;
t->tree[t->top].r = NULL;
t->tree[t->top].n = m;
t->tree[t->top].o = 0;
}
else
{
u = (struct Tree *)malloc(sizeof(struct Tree));
v = (struct Tree *)malloc(sizeof(struct Tree));
w = (struct Tree *)malloc(sizeof(struct Tree));
memcpy(v, &t->tree[t->top--], sizeof(struct Tree));
memcpy(u, &t->tree[t->top], sizeof(struct Tree));
w->o = c;
switch (c)
{
case '+':
w->n = u->n + v->n;
break;
case '-':
w->n = u->n - v->n;
break;
case '*':
w->n = u->n * v->n;
break;
case '/':
w->n = u->n / v->n;
break;
}
w->l = (struct Tree *)&u;
w->r = (struct Tree *)&v;
memcpy(&t->tree[t->top], w, sizeof(struct Tree));
}
}
void pushstack_o(stack *o, struct tree_pro *t, int m,
char c)
{
// stack in member and operation
if (m <= o->sto[o->top].num && o->sto[o->top].num != 3)
{
for (; o->sto[o->top].num != 3;)
{
if (m > o->sto[o->top].num)
break;
push_tree(t, -1, o->sto[o->top].op);
o->top--;
if (o->top == -1)
break;
}
}
if (m == 4)
{
// right round
for (; o->sto[o->top].num != 3; o->top--)
{
push_tree(t, -1, o->sto[o->top].op);
}
o->top--;
}
else
{
o->sto[++o->top].num = m; // save number and operation
o->sto[o->top].op = c;
}
}
void print_tree(struct tree_pro *t)
{
if (t->tree[t->top].o != 0)
printf("%c ", t->tree[t->top].o);
else
printf("%d ", t->tree[t->top].n);
if (u->o != 0)
printf("%c ", u->o);
else
printf("%d ", u->n);
if (v->o != 0)
printf("%c \n", v->o);
else
printf("%d \n", v->n);
printf("%d", t->tree[t->top].n);
}
int main()
{
initstack(&o); // init all, num, operation
t.top = -1;
while ((c = getchar()) != '=')
{
if (c >= '0' && c <= '9')
{
for (i = 0; c >= '0' && c <= '9'; c = getchar()) // number produce
n = c - '0' + n * 10;
ungetc(c, stdin);
push_tree(&t, n, 0); // stack in
n = 0;
}
else if (c != ' ')
{
switch (c)
{
// distribute number
case '+':
pushstack_o(&o, &t, 1, c);
break;
case '-':
pushstack_o(&o, &t, 1, c);
break;
case '*':
pushstack_o(&o, &t, 2, c);
break;
case '/':
pushstack_o(&o, &t, 2, c);
break;
case '(':
pushstack_o(&o, &t, 3, c);
break;
case ')':
pushstack_o(&o, &t, 4, c);
break;
}
}
}
for (; o.top != -1; o.top--)
{
push_tree(&t, -1, o.sto[o.top].op);
}
print_tree(&t);
return 0;
}
BUAAer?
边栏推荐
- Princeton University, Peking University & UIUC | offline reinforcement learning with realizability and single strategy concentration
- Four logs of MySQL server layer
- Shell pass parameters
- ESBuild & SWC浅谈: 新一代构建工具
- Shell 传递参数
- Esbuild & SWC: a new generation of construction tools
- SD卡報錯“error -110 whilst initialising SD card
- MySQL Server层四个日志
- 深入探究指针及指针类型
- SAP ALV颜色代码对应颜色(整理)
猜你喜欢
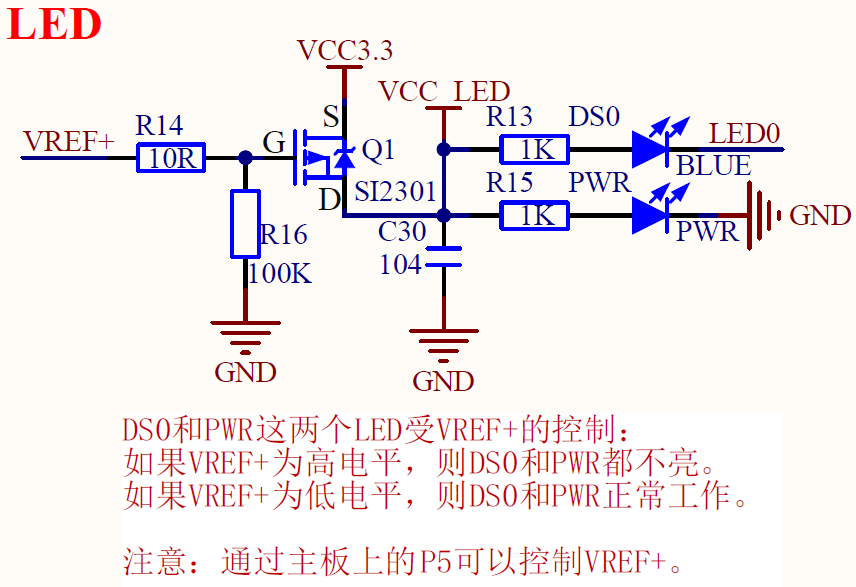
2. GPIO related operations

施努卡:3d视觉检测应用行业 机器视觉3d检测
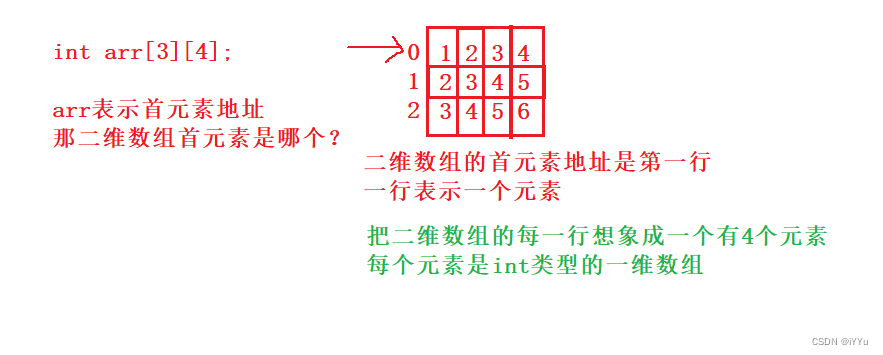
Explore pointers and pointer types in depth
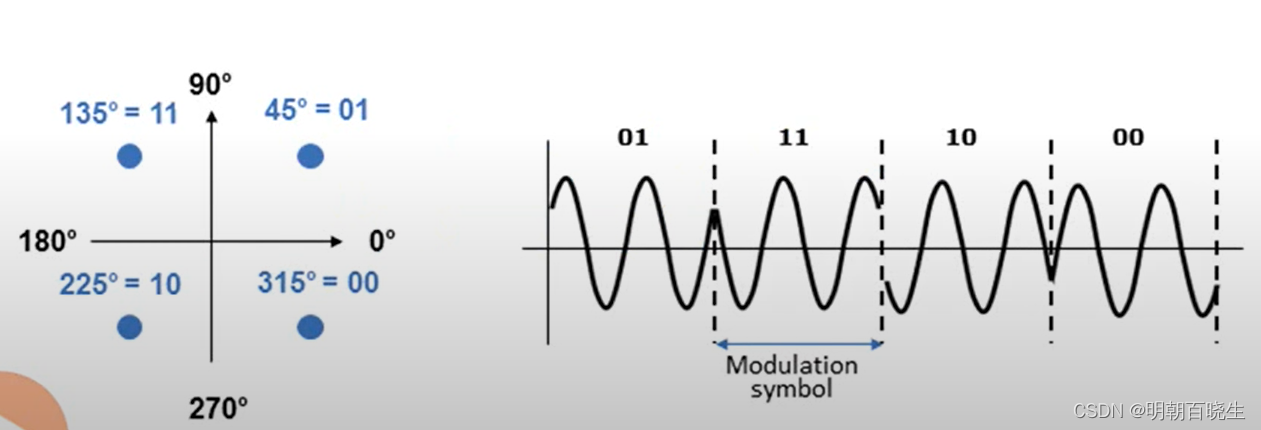
NR modulation 1

NR modulation 1
Tomb. Weekly update of Finance (February 7 - February 13)

Svg drag point crop image JS effect
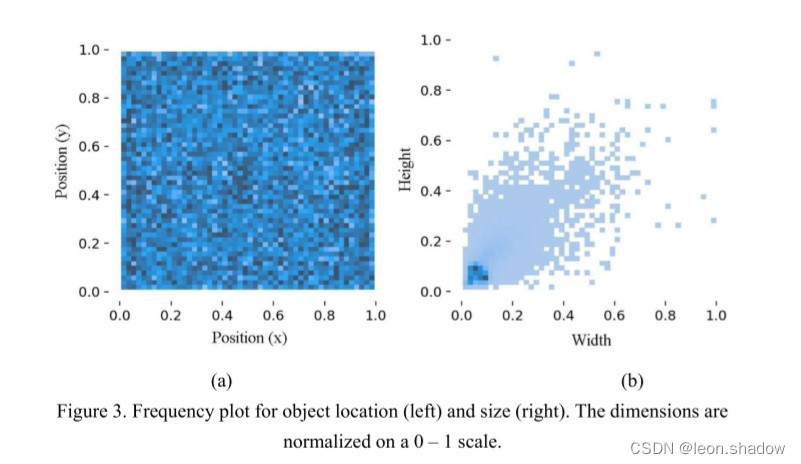
Remote Sensing Image Super-resolution and Object Detection: Benchmark and State of the Art

Exness foreign exchange: the governor of the Bank of Canada said that the interest rate hike would be more moderate, and the United States and Canada fell slightly to maintain range volatility

svg拖动点裁剪图片js特效
随机推荐
Canvas cut blocks game code
2、GPIO相关操作
3.1 detailed explanation of rtthread serial port device (V1)
Pointer written test questions ~ approaching Dachang
The solution of permission denied (750 permissions should be used with caution)
2.1 rtthread pin设备详解
【RISC-V】外部中断
Tidb ecological tools (backup, migration, import / export) collation
SAP ALV颜色代码对应颜色(整理)
Performance analysis of user login TPS low and CPU full
【SLAM】ORB-SLAM3解析——跟踪Track()(3)
JS音乐在线播放插件vsPlayAudio.js
Svg drag point crop image JS effect
[rust notes] 18 macro
真机无法访问虚拟机的靶场,真机无法ping通虚拟机
Problems encountered in 2022 work IV
MySQL Server层四个日志
Remote Sensing Image Super-resolution and Object Detection: Benchmark and State of the Art
MPLS experiment
Four logs of MySQL server layer