当前位置:网站首页>ArabellaCPC 2019(补题)
ArabellaCPC 2019(补题)
2022-07-06 03:05:00 【WDLieqi】
D. Meeting Bahosain
题目大意
a,b两个数组,其中b数组里面的元素都是不同的,问我们是不是可以在a里面选一个元素,用b里面的元素对其进行无限次的加减,最后让a数组元素相同。比赛时根本不懂题目意思,裂开。
解题思路
要让所有元素相同,那么a[i] - a[j] (i, j 为任意的数)就要等于x1 * b1 + x2 * b2 + x3 * b3 + … + xn * bn。这里就要引入一个定理:a * x + b * y = gcd(a, b) 一定有解。代入进去我们可以得出 x1 * b1 + x2 * b2 + x3 * b3 + … + xn * bn = gcd(b1, b2, b3, …, bn)一定有解,这里因为乘数是自己取得,所以可得出 a[ i ] - a[ j ] = x * (gcd(b1, b2, …, bn)),x是任意常数。
最后就得出结论了,只要所有的a[ i ] - a[ j ]整除gcd(b1, b2, …, bn)就可以了。
代码
#include <bits/stdc++.h>
using namespace std;
#define IOS \
ios::sync_with_stdio(false); \
cin.tie(0); \
cout.tie(0);
//#define For(i, k, n) for (int i = k; i < n; i ++)
//#define FOR(i, k, n) for (int i = k; i <= n; i ++)
#define P acos(-1);
typedef long long LL;
typedef unsigned long long ULL;
#define PII pair<int, int>
#define PDD pair<double, double>
#define Pll pair<LL, LL>
typedef unsigned long long Uint;
const double eps = 1e-7;
const int M = 1e6 + 10, mod = 1000000007;
const int inf = 0x3f3f3f3f;
int dx[4] = {0, 1, -1, 0}, dy[4] = {1, 0, 0, -1};
int lowbit(int x) { return (x & -x); };
// 以上可忽略
const int N = 1e6 + 10;
int a[N], b[N];
void solve()
{
int n, k;
cin >> n >> k;
for (int i = 0; i < n; i ++)
cin >> a[i];
int res = 0;
for (int i = 0; i < n; i ++)
cin >> b[i], res = (res == 0) ? b[i] : __gcd(res, b[i]);
for (int i = 1; i < n; i ++)
{
if ((a[i] - a[i - 1]) % res != 0)
{
puts("No");
return;
}
}
puts("Yes");
}
int main()
{
IOS
int T = 1;
//cin >> T;
//scanf("%d", &T);
while (T--)
{
solve();
}
return 0;
}
I. Bashar and Hamada
题目大意
k(2 <= k <= n) 长度的数字问相互之间的差值的绝对值的最大值是多少。
解题思路
首先我们应该明白顺序是不影响大小的。然后再找一个规律:
假定一组数据 {1,2,3,4,5,7},开始ans=0;
开始:ans+= |1-7|
插入5: ans+=|5-1|+|5-7|=|1-7|
插入2: ans+=|2-1|+|2-7|+|2-5|==|1-7|+|2-5|
插入4: ans+=|4-1|+|4-7|+|4-5|+|4-2|==|1-7|+|2-5|
插入3: ans+=|3-1|+|3-7|+|3-5|+|3-2|+|3-4|==|1-7|+|2-5|+|3-4|
这样列出来就很明显了。奇数次插入,要加的数保存不变。
可以看到每插入2个就增加一个组合,只要每次加入的组合为最大,就能保证答案最大。
每次组合都选差最大的,排序后,就是左右各一个。
思路转载自这个博客:
https://www.cnblogs.com/studyshare777/p/12766707.html
代码
#include <bits/stdc++.h>
using namespace std;
#define IOS \
ios::sync_with_stdio(false); \
cin.tie(0); \
cout.tie(0);
//#define For(i, k, n) for (int i = k; i < n; i ++)
//#define FOR(i, k, n) for (int i = k; i <= n; i ++)
#define P acos(-1);
typedef long long LL;
typedef unsigned long long ULL;
#define PII pair<int, int>
#define PDD pair<double, double>
#define Pll pair<LL, LL>
typedef unsigned long long Uint;
const double eps = 1e-7;
const int N = 3e5 + 10, M = 1e6 + 10, mod = 1000000007;
const int inf = 0x3f3f3f3f;
int dx[4] = {0, 1, -1, 0}, dy[4] = {1, 0, 0, -1};
int lowbit(int x) { return (x & -x); };
LL f[N];
void solve()
{
LL n;
cin >> n;
for (int i = 1; i <= n; i ++)
cin >> f[i];
sort(f + 1, f + 1 + n);
LL ans = 0, tot = 0;
ans = f[n] - f[1];
tot = ans;
cout << ans << ' ';
int r = n - 1, l = 2;
for (int i = 1; i < n - 1; i ++)
{
if (!(i & 1))
tot += f[r --] - f[l ++];
ans += tot;
cout << ans << ' ';
}
}
int main()
{
IOS
int T = 1;
//cin >> T;
//scanf("%d", &T);
while (T--)
{
solve();
}
return 0;
}
边栏推荐
- 【Unity3D】GUI控件
- 继承day01
- [kubernetes series] learn the exposed application of kubernetes service security
- Introduction to robotframework (II) app startup of appui automation
- RobotFramework入门(二)appUI自动化之app启动
- 【Kubernetes 系列】一文學會Kubernetes Service安全的暴露應用
- #PAT#day10
- SD卡报错“error -110 whilst initialising SD card
- BUUCTF刷题笔记——[极客大挑战 2019]EasySQL 1
- Microsoft speech synthesis assistant v1.3 text to speech tool, real speech AI generator
猜你喜欢
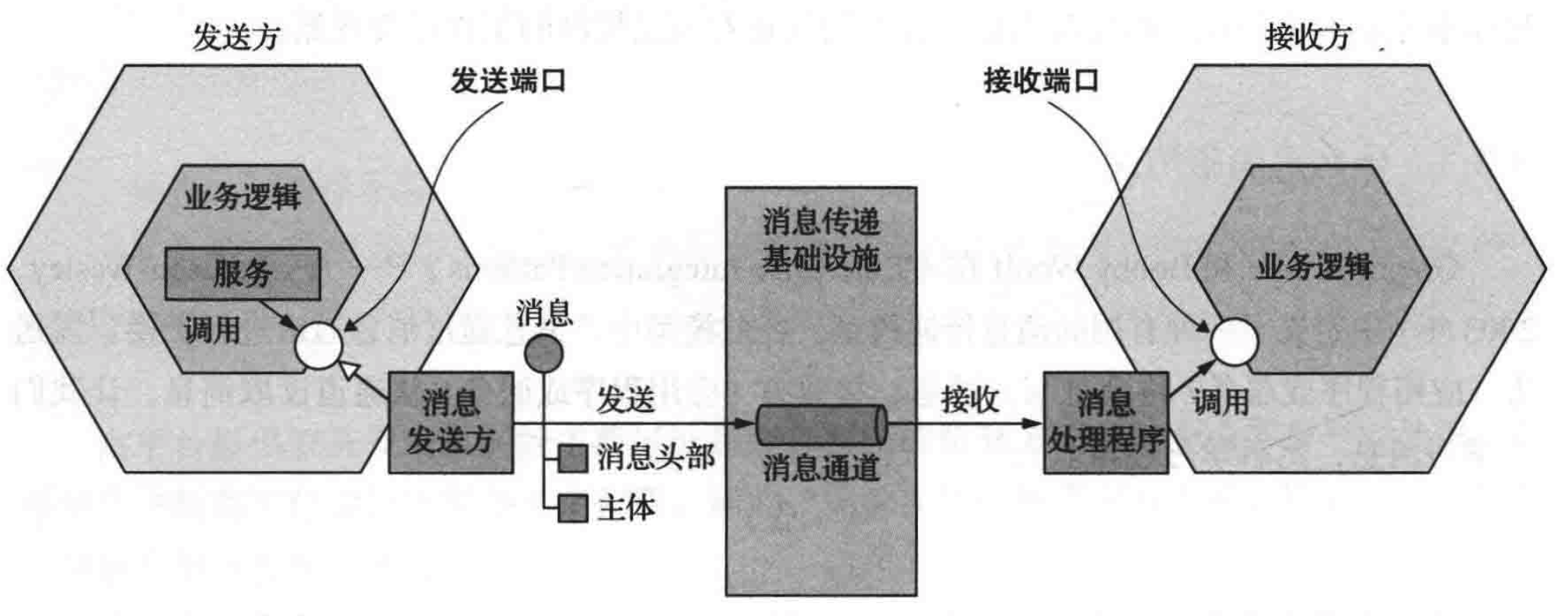
Communication between microservices
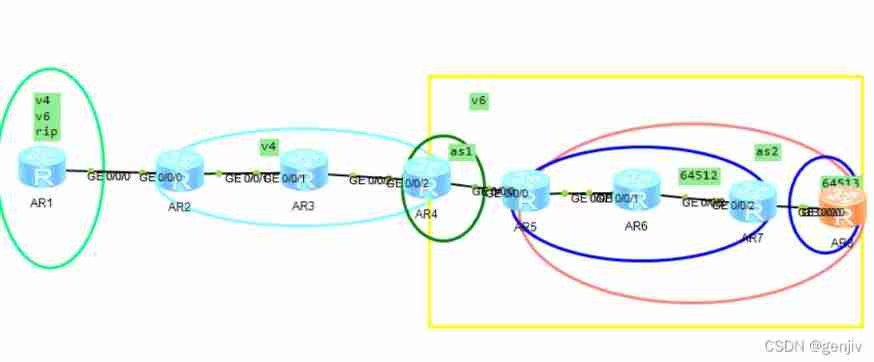
IPv6 jobs
How to do function test well

Codeworks 5 questions per day (1700 average) - day 6
![Huawei, H3C, Cisco command comparison, mind map form from the basic, switching, routing three directions [transferred from wechat official account network technology alliance station]](/img/3b/385d19e51340ecd6281df47b39f40c.png)
Huawei, H3C, Cisco command comparison, mind map form from the basic, switching, routing three directions [transferred from wechat official account network technology alliance station]
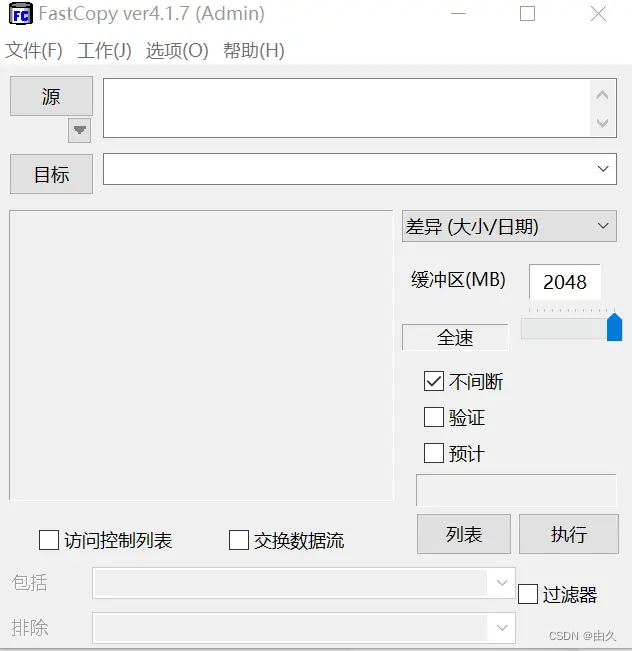
A copy can also produce flowers
Universal crud interface
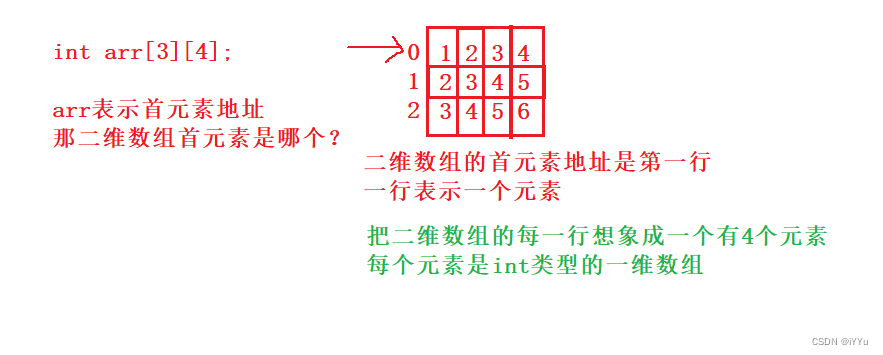
深入探究指针及指针类型
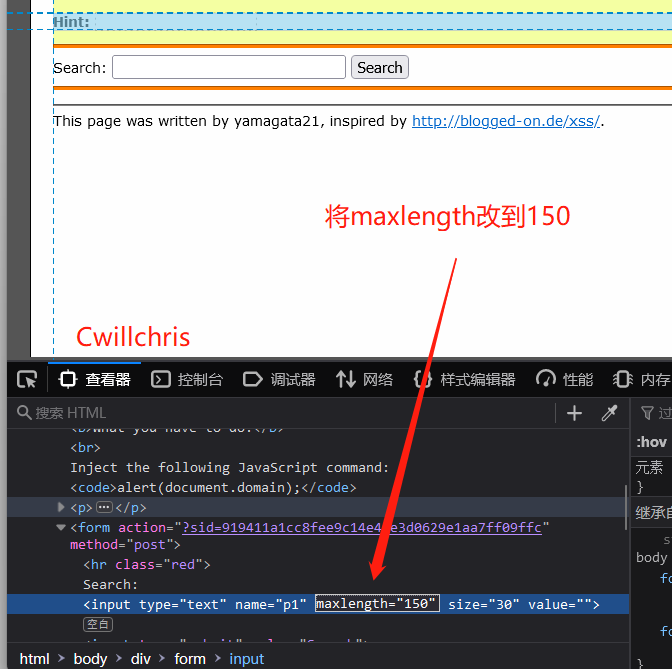
XSS challenges bypass the protection strategy for XSS injection
如何精准识别主数据?
随机推荐
RobotFramework入门(一)简要介绍及使用
MySQL advanced notes
【概念】Web 基础概念认知
Single instance mode of encapsulating PDO with PHP in spare time
Add one to non negative integers in the array
Microsoft speech synthesis assistant v1.3 text to speech tool, real speech AI generator
My C language learning record (blue bridge) -- on the pointer
2.13 simulation summary
Redis SDS principle
Universal crud interface
[concept] Web basic concept cognition
1. Dynamic parameters of function: *args, **kwargs
银行核心业务系统性能测试方法
Prototype design
[Chongqing Guangdong education] higher mathematics I reference materials of Southwest Petroleum University
如何做好功能测试
Problems encountered in 2022 work IV
【 kubernets series】 a Literature Study on the Safe exposure Applications of kubernets Service
CSP numeric sort
NR modulation 1
