Manhattan distance and Manhattan rectangle - print back font matrix

Food Guide ：

Leetcode The column opens , Because the blogger is closed at the end of the period , So only one question per day
Try to solve more than one problem , First say the train of thought. , Then the code realizes , Necessary comments will be added
Grammar or STL The content will be highlighted at the attention point , Novice friendly
Welcome to the blogger's magic tricks column , Detailed explanation of connotation algorithm foundation and code template

Title Description ：

• Input integer N, Output one N Two dimensional array of order glyphs .

  The outermost layer of the array is 1, The outer layer is 2, And so on .

  Input format
  The input contains multiple lines , Each line contains an integer N.
  When the input behavior N=0 when , End of input , And the bank doesn't need to do anything .

  Output format
  For each input integer N, Output one that meets the requirements N Order two-dimensional array .
  Each array takes N That's ok , Each row contains N Integers separated by spaces .
  After the output of each array , Output a blank line .

  Data range
  0≤N≤100
  sample input ：
  1
  2
  3
  4
  5
  0
  sample output ：
  1

  1 1
  1 1

  1 1 1
  1 2 1
  1 1 1

  1 1 1 1
  1 2 2 1
  1 2 2 1
  1 1 1 1

  1 1 1 1 1
  1 2 2 2 1
  1 2 3 2 1
  1 2 2 2 1
  1 1 1 1 1

• Title source ：https://www.acwing.com/problem/content/755/

Topic analysis ：

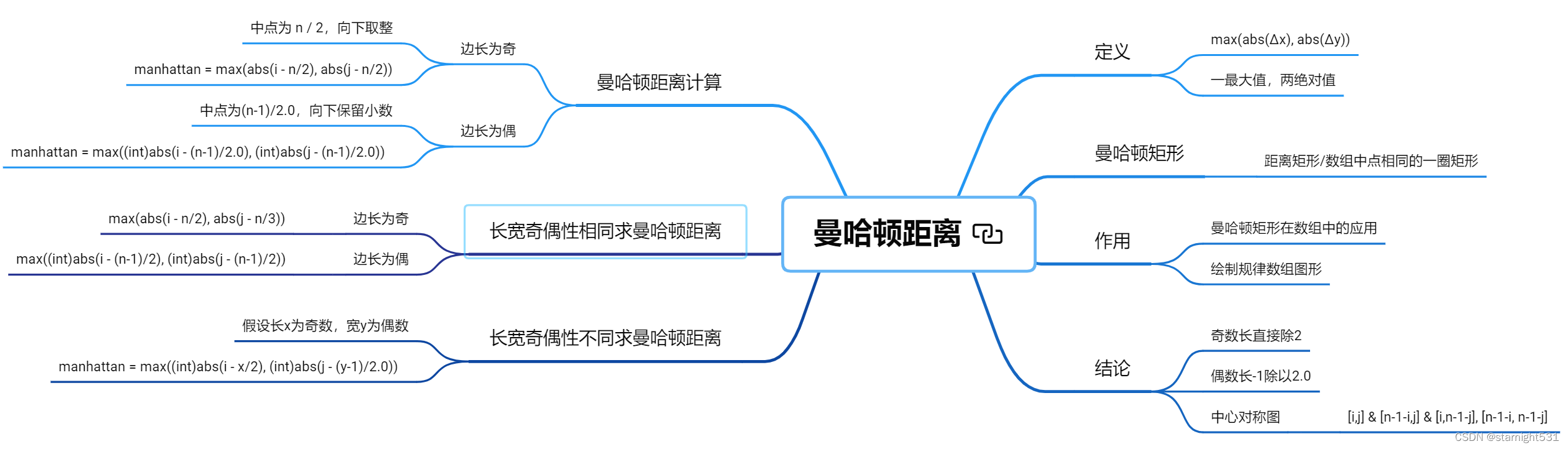
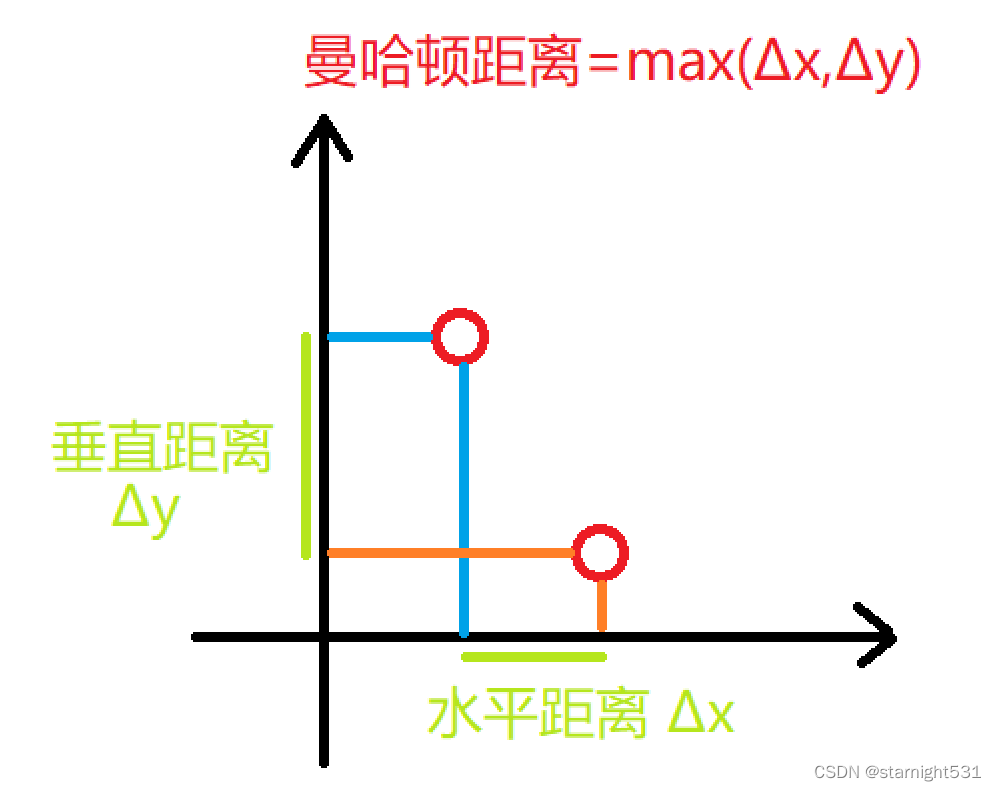
Law 1 ： Manhattan distance

• Manhattan distance is two points in the vertical coordinate system ,x & y Direction Maximum projection distance
  

• Apply to array / Matrix , Manhattan sets points at the same distance into A circle of rectangles around the center of the matrix ,

  When calculating Manhattan distance , Number of district branches required / Parity of column numbers ：
  

Law two ： The relationship between array subscript and value

• Manhattan distance is actually the conclusion of the research on the relationship between array subscripts and values

  When you don't know the distance from Manhattan , Try exploring manually , Other conclusions of non Manhattan distance may be drawn

Direction 1： Deduce the relationship with distance

1. The graph is symmetrical about the center
   Points that do not cross the center line are used i Calculation , Cross the center line with n-1-i Calculation ,
   be For all points , or i and n-1-i/n-i Calculate once each , Take the largest of the two / Small value , Or use absolute value
   2. For points that do not cross the center line , Use examples to explore
   n = 5 when ,n/2 = 2, Midpoint is (2, 2)
   The first point arr[0][0] = 1, Distance to midpoint Δx = Δy =2
   Second points arr[1][0] = 1, From the end Δx = 2, Δy =1
   The third point arr[0][1] = 1, From the end Δx = 1, Δy =2
   Determine the calculation formula ：n/2 - max(abs(x-n/2) , abs(y-n/2)) + 1
   3. For the point passing the center line , Use examples to explore
   n = 5 when ,n/2 = 2, Midpoint is (2, 2)
   The first point arr[4][4] = 1, Distance to midpoint Δx = Δy =2
   Second points arr[3][4] = 1, From the end Δx = 1, Δy =2
   The third point arr[4][3] = 1, From the end Δx = 2, Δy =1
   Determine the calculation formula ：n/2 - max(abs(x-n/2) , abs(y-n/2)) + 1

• After completing the derivation with distance , You will find that you are pushing Manhattan distance ,

Direction 2： Just look at the relationship between subscript and value

• n = 5 when ：
  1. For points that do not cross the center line , Use examples to explore ：
     The first point arr[0][0] = 1,1 = max/min(x + 1, y + 1)
     Second points arr[1][0] = 1,1 = min(x + 1, y + 1)
     The third point arr[0][1] = 1,1 = min(x + 1, y + 1)
     The stone hammer adopts min(x + 1, y + 1)
  2. For the point passing the center line , Use examples to explore ：
     The first point arr[4][4] = 1,1 = max/min(n-x, n-y)
     Second points arr[3][4] = 1,1 = min(n-x, n-y)
     The third point arr[4][3] = 1,1 = min(n-x, n-y)
     The stone hammer adopts min(n-x, n-y)
     3. Look at all points as a whole ：
     Now there are two options ：min(x + 1, y + 1) & min(n-x, n-y)
     Check to see if / What kind of ？
     For point arr[3][4],min(x + 1, y + 1) = 4, min(n-x, n-y) = 1
     For point arr[0][0],min(x + 1, y + 1) = 1, min(n-x, n-y) = 5
     It is found that the minimum value of the two schemes is taken for each point , So come to the conclusion ：
• So for all points ：arr[i][j] = min(min(x + 1, y + 1) , min(n-x, n-y));

Law three ： Symmetric simplification （ Strictly speaking, it belongs to skill rather than method ）

• Centrosymmetric image , Filling in a little is equivalent to filling in 4 spot .

  With n = 5 Rectangle of , View symmetrical 4 Dot subscript relation ：
  

• When filling in the value of a quadrant , Manhattan matrix method can be used / The relationship between subscript and value

  This technique increases the time complexity , Reduce the time to a quarter of the original

  It can also be used as a starting point for thinking when simplifying and finding rules in the following topics

Algorithm template :

• Manhattan distance + Law of central symmetry Itself is the basic algorithm , No template

Code implementation ：

Law 1 ：

import java.util.Scanner;
import java.lang.Math;
public class Main{
    
    public static void main(String[] args){
    
        Scanner sc = new Scanner(System.in);
        while(true){
    
            int n = sc.nextInt();
            if (n == 0) return;     // Read the termination exit 
            for(int i=0; i<n; i++){
    
                for(int j=0; j<n; j++){
    
                    if(n % 2 == 1)
                    // Manhattan is closer , Large value , A distance of 0 The value is (n+1)/2
                    System.out.print((n+1)/2 - Math.max(Math.abs(n/2-i), Math.abs(n/2-j)) +" ");
                    else 
                    // Manhattan is closer , Large value , A distance of 0 The value is n/2
                    System.out.print((n/2) - Math.max((int)Math.abs((n-1)/2.0-i), (int)Math.abs((n-1)/2.0-j)) +" ");
                }
                System.out.println();
            }
            System.out.println();
        }
    }
}

Law two ：

• Subscript and value relationship ：Math.min(Math.min(i+1, j+1), Math.min(n-i, n-j))

import java.util.Scanner;
import java.lang.Math;
public class Main{
    
    public static void main(String[] args){
    
        Scanner sc = new Scanner(System.in);
        while(true){
    
            int n = sc.nextInt();
            if (n == 0) return;     // Read the termination exit 
            for(int i=0; i<n; i++){
    
                for(int j=0; j<n; j++){
    
                    System.out.print(Math.min(Math.min(i+1, j+1), Math.min(n-i, n-j))+" ");
                }
                System.out.println();
            }
            System.out.println();
        }
    }
}

Law three ：

• Manhattan distance filling ：

import java.util.Scanner;
import java.lang.Math;
public class Main{
    
    public static void main(String[] args){
    
        Scanner sc = new Scanner(System.in);
        while(true){
    
            int n = sc.nextInt();
            if (n == 0) return;     // Read the termination exit 
            int[][] arr = new int[n][n];
            
            // Even rows , Such as 4 That's ok 4 Column , Just fill in 0~1 That's ok  & 0~1 Column 
            if(n % 2 == 0){
    
                for(int i=0; i<n/2; i++){
    
                    for(int j=0; j<n/2; j++){
    
                        arr[i][j] = arr[n-1-i][n-1-j] 
                        = arr[n-1-i][j] = arr[i][n-1-j] 
                        = n/2 - Math.max(Math.abs((int)((n-1)/2.0 - i)), Math.abs((int)((n-1)/2.0 - j)));
                    }
                }
            }
            // Odd row , Such as 5 That's ok 5 Column , It needs to be filled in 0~2 That's ok  & 0~2 Column 
            else{
    
                for(int i=0; i<=n/2; i++){
    
                    for(int j=0; j<=n/2; j++){
    
                        arr[i][j] = arr[n-1-i][n-1-j] 
                        = arr[n-1-i][j] = arr[i][n-1-j] 
                        = (n+1)/2 - Math.max(Math.abs(n/2 - i), Math.abs(n/2 - j));
                    }
                }
            }
            for(int i=0; i<n; i++){
    
                for(int j=0; j<n; j++){
    
                    System.out.print(arr[i][j]+" ");
                }
                System.out.println();
            }
            System.out.println();
        }
    }
}

• Fill in the relationship between subscript and value ：

import java.util.Scanner;
import java.lang.Math;
public class Main{
    
    public static void main(String[] args){
    
        Scanner sc = new Scanner(System.in);
        while(true){
    
            int n = sc.nextInt();
            if (n == 0) return;     // Read the termination exit 
            int[][] arr = new int[n][n];
            
            // Even rows , Such as 4 That's ok 4 Column , Just fill in 0~1 That's ok  & 0~1 Column 
            if(n % 2 == 0){
    
                for(int i=0; i<n/2; i++){
    
                    for(int j=0; j<n/2; j++){
    
                        arr[i][j] = arr[n-1-i][n-1-j] = arr[n-1-i][j] = arr[i][n-1-j] = Math.min(Math.min(i+1, j+1), Math.min(n-i, n-j));
                    }
                }
            }
            // Odd row , Such as 5 That's ok 5 Column , It needs to be filled in 0~2 That's ok  & 0~2 Column 
            else{
    
                for(int i=0; i<=n/2; i++){
    
                    for(int j=0; j<=n/2; j++){
    
                        arr[i][j] = arr[n-1-i][n-1-j] = arr[n-1-i][j] = arr[i][n-1-j] = Math.min(Math.min(i+1, j+1), Math.min(n-i, n-j));
                    }
                }
            }
            for(int i=0; i<n; i++){
    
                for(int j=0; j<n; j++){
    
                    System.out.print(arr[i][j]+" ");
                }
                System.out.println();
            }
            System.out.println();
        }
    }
}

Be careful ：

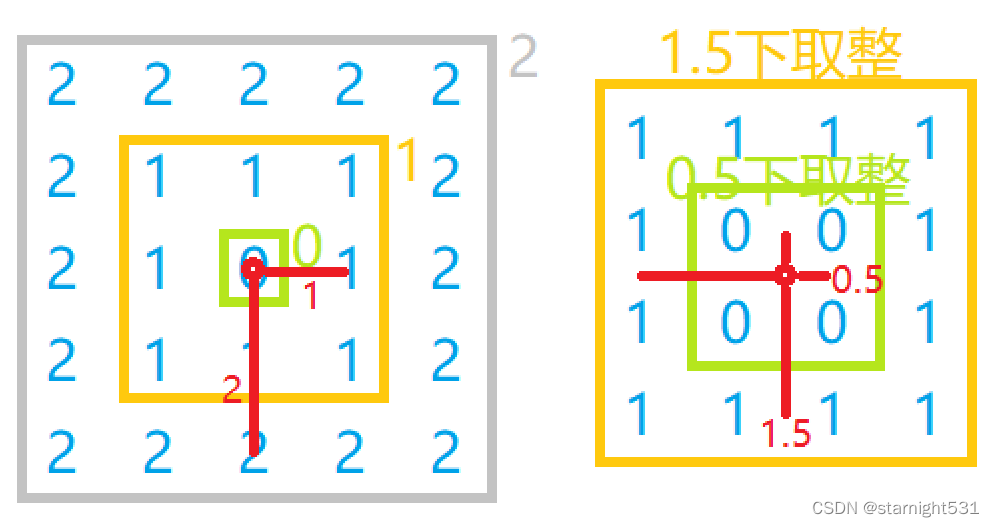
• Manhattan distance formula ：

  • That's ok / The number of columns is odd ：
    manhattan = max(abs(x - n/2), abs(y - n/2));
    The midpoint n/2 Rounding down , And the result itself is an integer
  • That's ok / The number of columns is even ：
    manhattan = max((int)abs(x - (n-1)/2.0), (int)abs(y-(n-1)/2.0));
    That is, the midpoint is a decimal without rounding , and x - (n-1)/2.0 The result is rounded down
  • It can be abbreviated as , Divide the midpoint of an odd number directly 2, Even midpoint -1 Divide 2.0

• For those with high safety requirements Java
  double and int operation , Is first Int Integer raised to double And again double operation
  take Double use (int) The explicit type is converted to int, It is also rounded down by default