The connection and solution between the shortest Hamilton path and the traveling salesman problem

Preface

I found that many blogs either post code directly , Or it's right dp Explain the formula , It makes people feel speechless without saying why they got this formula , That might be why c standing

The shortest Hamilton route

Title Transfer door
The title means from 0 From point to n-1 The shortest point Hamilton route , We analyze it from the perspective of set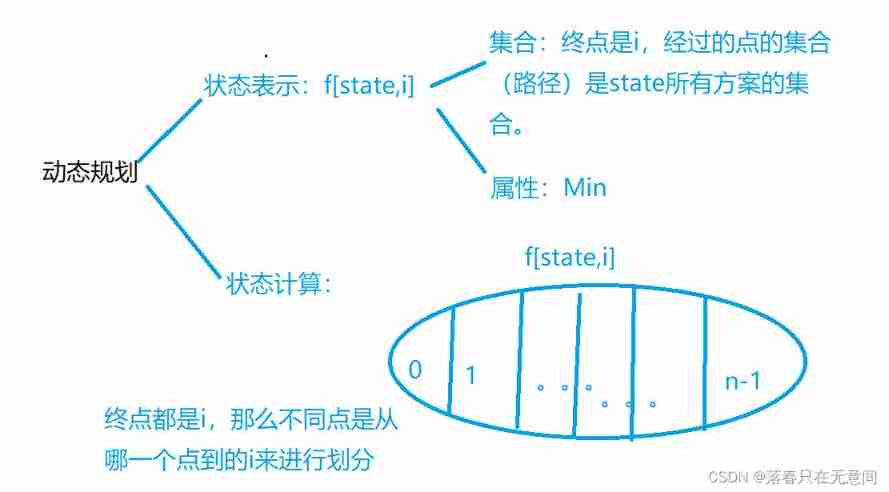

So what are the conditions for this transition

1. In the current path state ,i The corresponding position needs to be 1, That is, the end point of the starting point needs to appear on the path .
2. For intermediate nodes k for , Each point can only appear once , So let's get rid of i Then the set of corresponding paths needs to have nodes k.

If the above conditions are met, there can be a transfer formula ：
$dp[i][j]=min(dp[i][j],dp[i-(1<<j)][k]+w[k][j]$

Let's take the outer cycle as the last , That is to say state State transition means that all points pass through once , The second cycle is n-1 That is, the end of the question , We're enumerating k That is, we are considering which point is better to arrive at the end , If we choose a point , Then there will be the same sub problem at this point .

Code ：

#include<iostream>
#include<stdio.h>
#include<cstring>
using namespace std;

const int N = 20 ,M = 1<<20;
int f[M][N] ,weight[N][N];
int n;


int main(){
    
    scanf("%d",&n);
    for(int i=0;i<n;++i)
    for(int j = 0;j<n;++j)
    scanf("%d",&weight[i][j]);
    memset(f,0x3f,sizeof f);
    f[1][0] = 0;
    for(int i=0;i< 1<<n;++i)
    for(int j=0;j<n;++j)if(i>>j &1) //  There are j
    for(int k = 0;k<n;++k)if(i-(1<<j)>>k & 1 ) // There are k, But there is no j
    f[i][j] = min(f[i][j],f[i-(1<<j)][k] + weight[k][j]);//i-(1<<j)  Already in if Prove that the location exists 
    
    printf("%d\n",f[(1<<n)-1][n-1]);
    return 0;
}

Travel agent problem

Why should I compare the problem of travel agents with Hamilton The paths are written together , The traveling salesman problem is abstractly a starting point arbitrary and the end point is its own Hamilton route .
Let's think back to Hamilton In the path ,$dp[i][j]$ What arrays mean is ： from 0 Appear to the end j, And each point only goes once i Shortest path , Then we are finishing the calculation Hamilton After path , We just need to add a line from the end to 0 The path of , Then we can form this starting point arbitrary traveling salesman problem .
So here comes the question , Someone may ask why it is connected to 0 It can't be anything else ,
First of all, we know that if we choose arbitrarily at the starting point, then every point can go once , Then the end is definitely not this point , Then we can specify that the last point is 0( Then add 0 The distance to the starting point ) Because the first point of the starting point is arbitrary , Finally, we get a minimum value in any possibility .

So let's turn over this idea , We can make the point pointing to the starting point arbitrary , Then the first point pointed by the starting point will not be arbitrary ( Recall what probability theory learned ), Therefore, we can set the first point of our starting point 0, Then we can transform this part into Hamilton Path . Here's the code

Code ：

#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 16, M = 1 << N, INF = 0x3f3f3f3f;
int n, m, g[N][N];
int f[M][N] ;

int main() {
    
	cin >> n >> m;
	memset(g, 0x3f, sizeof g );
	memset(f, 0x3f, sizeof f);
	while (m--) {
    
		int a, b, c;
		cin >> a >> b >> c;
		g[a][b] = c;
	}
	for (int i = 0 ; i < n ; ++i)
		g[i][i] = 0;
	f[1][0] = 0;
	for (int i = 0 ; i < 1 << n ; ++i)
		for (int j = 0 ; j < n ; ++j)
			if (i >> j & 1) {
    
				for (int k = 0 ; k < n ; ++k)
					if ((i - (1 << j)) >> k & 1)
						f[i][j] = min(f[i][j], f[i - (1 << j)][k] + g[k][j]);
			}
	int res = INF;
	for (int i = 0 ; i < n ; ++i)
		res = min(res, f[(1 << n) - 1][i] + g[i][0]);
	if (res == INF)
		cout << -1 << endl;
	else
		cout << res << endl;
	return 0;
}