当前位置:网站首页>C language [23] classic interview questions [Part 2]
C language [23] classic interview questions [Part 2]
2022-07-07 01:43:00 【Choice~】
13. choice 、 Insert 、 Bubble sort
explain
Selection sort (Selection sort)、 Insertion sort (Insertion sort) Sort with bubble (Bubble sort) These three sorting methods are the three basic sorting methods that beginners must know , They are not practical because they are not fast ( The average and fastest time complexity are O(n2)), However, the way they are sorted is worth observing and discussing .
solution
Select sort divides the object to be sorted into two parts , One is sorted , One is unordered , Select a minimum value from the back-end unordered part , And put the last one in the sorted part of the front end , for example :
Before ordering :70 80 31 37 10 1 48 60 33 80
[1] 80 31 37 10 70 48 60 33 80 Select the minimum value 1
[1 10] 31 37 80 70 48 60 33 80 Select the minimum value 10
[1 10 31] 37 80 70 48 60 33 80 Select the minimum value 31
[1 10 31 33] 80 70 48 60 37 80 …
[1 10 31 33 37] 70 48 60 80 80 …
[1 10 31 33 37 48] 70 60 80 80 …
[1 10 31 33 37 48 60] 70 80 80 …
[1 10 31 33 37 48 60 70] 80 80 …
[1 10 31 33 37 48 60 70 80] 80 …
Insertion sort It's like playing park , We divided the cards into two piles , Each time from the back of a pile of cards out of the front card , Then insert the appropriate position in the front stack of cards , for example :
Before ordering :92 77 67 8 6 84 55 85 43 67
[77 92] 67 8 6 84 55 85 43 67 take 77 Insert 92 front
[67 77 92] 8 6 84 55 85 43 67 take 67 Insert 77 front
[8 67 77 92] 6 84 55 85 43 67 take 8 Insert 67 front
[6 8 67 77 92] 84 55 85 43 67 take 6 Insert 8 front
[6 8 67 77 84 92] 55 85 43 67 take 84 Insert 92 front
[6 8 55 67 77 84 92] 85 43 67 take 55 Insert 67 front
[6 8 55 67 77 84 85 92] 43 67 …
[6 8 43 55 67 77 84 85 92] 67 …
[6 8 43 55 67 67 77 84 85 92] …
Bubble sorting method
seeing the name of a thing one thinks of its function , When sorting , The largest element moves to the right like a bubble , It uses the method of comparing adjacent elements , Swap the large elements to the right , So the big elements will keep moving to the right , Until it is in place . The basic bubble sorting method can use flags to slightly reduce the comparison time , After searching the array, there is no exchange , Indicates the sorting is complete , There is no need to do the following loop comparison and exchange , for example :
Before ordering :95 27 90 49 80 58 6 9 18 50
27 90 49 80 58 6 9 18 50 [95] 95 Surfaced
27 49 80 58 6 9 18 50 [90 95] 90 Surfaced
27 49 58 6 9 18 50 [80 90 95] 80 Surfaced
27 49 6 9 18 50 [58 80 90 95] …
27 6 9 18 49 [50 58 80 90 95] …
6 9 18 27 [49 50 58 80 90 95] …
6 9 18 [27 49 50 58 80 90 95]
Because there will be no exchange next , Sorting ends early . In the example above , It also adds an idea , Is when it goes to i And i+1 There is no exchange action , Means the next i+2 to n It has been sorted , This also improves the efficiency of bubble sorting .
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#define MAX 10
#define SWAP(x,y) {
int t; t = x; x = y; y = t;}
void selsort(int[]); // Selection sort
void insort(int[]); // Insertion sort
void bubsort(int[]); // Bubble sort
int main(void) {
int number[MAX] = {
0};
int i;
srand(time(NULL));
printf(" Before ordering :");
for(i = 0; i < MAX; i++) {
number[i] = rand() % 100;
printf("%d ", number[i]);
}
printf("\n Please select sort by :\n");
printf("(1) Selection sort \n(2) Insertion sort \n(3) Bubble sort \n:");
scanf("%d", &i);
switch(i) {
case 1:
selsort(number); break;
case 2:
insort(number); break;
case 3:
bubsort(number); break;
default:
printf(" Wrong option (1..3)\n");
}
return 0;
}
void selsort(int number[]) {
int i, j, k, m;
for(i = 0; i < MAX-1; i++) {
m = i;
for(j = i+1; j < MAX; j++)
if(number[j] < number[m])
m = j;
if( i != m)
SWAP(number[i], number[m])
printf(" The first %d Secondary ranking :", i+1);
for(k = 0; k < MAX; k++)
printf("%d ", number[k]);
printf("\n");
}
}
void insort(int number[]) {
int i, j, k, tmp;
for(j = 1; j < MAX; j++) {
tmp = number[j];
i = j - 1;
while(tmp < number[i]) {
number[i+1] = number[i];
i--;
if(i == -1)
break;
}
number[i+1] = tmp;
printf(" The first %d Secondary ranking :", j);
for(k = 0; k < MAX; k++)
printf("%d ", number[k]);
printf("\n");
}
}
void bubsort(int number[]) {
int i, j, k, flag = 1;
for(i = 0; i < MAX-1 && flag == 1; i++) {
flag = 0;
for(j = 0; j < MAX-i-1; j++) {
if(number[j+1] < number[j]) {
SWAP(number[j+1], number[j]);
flag = 1;
}
}
printf(" The first %d Secondary ranking :", i+1);
for(k = 0; k < MAX; k++)
printf("%d ", number[k]);
printf("\n");
}
}
14. Sequencing - Improved insertion sort
explain
The insertion sort method takes a value from the front end of the unsorted back half , Insert the appropriate position of the sorted first half , The concept is simple but not fast . One of the basic principles to speed up sorting , When the next sort is in progress , Try to use the results of the previous sort , To speed up sorting ,Shell The sorting method is to improve the insertion sorting method based on this concept .
solution
Shell The sorting method was originally D.L Shell On 1959 Put forward , Suppose the elements to be sorted are n individual , Not all elements are sorted at the same time each time , But take an interval .
Shell First set the interval to n/2, Then jump to insert sort , And then I'll take the interval n/4, Jump to sort , The recurrence interval is set to n/8、n/16, Until the interval is 1 The last sort after that ends , Because the last sorting action will sort the elements within the fixed interval , So when the interval gets smaller and smaller , The higher the probability that some elements will be in the right position , Therefore, the last few sorting actions can be greatly reduced . For example , Suppose there is an unordered number such as right :89 12 65 97 61 81 27 2 61 98 The total number of figures is 10 individual , So for the first time, we set the interval to 10 / 2 = 5, At this time, the interval is 5 In order of numbers , As shown below :
The parts connected by lines represent the parts to be sorted together , Then set the interval to 5 / 2 The business of , That is to say 2, Then the second insertion sorting object is as follows : The recurrence interval is set to 2 / 2 = 1, At this point, it is simply insert sorting , Because most of the elements have been roughly sorted ,
So the last insertion sort did little sort :
Set the interval to n / 2 yes D.L Shell Originally proposed , It is better to use this interval in textbooks , However Shell The key of sorting method is the selection of interval , for example Sedgewick It is proved that the following interval can speed up Shell The speed of sorting :
among 4*(2j)2 + 3*(2j) + 1 The total number of elements cannot be exceeded n value , Use the above formula to find j Future generations 4*(2j)2 + 3*(2j) + 1 Find the first interval , And then 2j Divide 2 Substitute in to find the second interval , And so on . Later, it was proved that there are other interval selection methods that can make Shell The speed of the sorting method is faster ; in addition Shell The concept of sequencing can also be used to improve bubble sequencing .
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#define MAX 10
#define SWAP(x,y) {
int t; t = x; x = y; y = t;}
void shellsort(int[]);
int main(void) {
int number[MAX] = {
0};
int i;
srand(time(NULL));
printf(" Before ordering :");
for(i = 0; i < MAX; i++) {
number[i] = rand() % 100;
printf("%d ", number[i]);
}
shellsort(number);
return 0;
}
void shellsort(int number[]) {
int i, j, k, gap, t;
gap = MAX / 2;
while(gap > 0) {
for(k = 0; k < gap; k++) {
for(i = k+gap; i < MAX; i+=gap) {
for(j = i - gap; j >= k; j-=gap) {
if(number[j] > number[j+gap]) {
SWAP(number[j], number[j+gap]);
}
else
break;
}
}
}
printf("\ngap = %d:", gap);
for(i = 0; i < MAX; i++)
printf("%d ", number[i]);
printf("\n");
gap /= 2;
}
}
15. Sequencing - Improved bubble sorting
explain
Let's take a look at the bubble sorting method introduced earlier :
for(i = 0; i < MAX-1 && flag == 1; i++) {
flag = 0;
for(j = 0; j < MAX-i-1; j++) {
if(number[j+1] < number[j]) {
SWAP(number[j+1], number[j]);
flag = 1;
}
}
}
In fact, this bubble sorting method is no longer a simple bubble sorting , It uses two methods: Flag and shift the right end to the left to improve the efficiency of sorting , and Shaker The sorting method uses the latter concept to further improve the bubble sorting method .
solution
In the bubble sort above , Switching does not continue until the last of the array , It will go on to MAX-i-1, So in the process of sorting , The ordered elements on the right side of the array will continue to increase , Make the number of sorting on the left decrease gradually , As our example shows :
Before ordering :95 27 90 49 80 58 6 9 18 50
27 90 49 80 58 6 9 18 50 [95] 95 Surfaced
27 49 80 58 6 9 18 50 [90 95] 90 Surfaced
27 49 58 6 9 18 50 [80 90 95] 80 Surfaced
27 49 6 9 18 50 [58 80 90 95] …
27 6 9 18 49 [50 58 80 90 95] …
6 9 18 27 [49 50 58 80 90 95] …
6 9 18 [27 49 50 58 80 90 95]
The parts enclosed in square brackets indicate that the sorting has been completed ,Shaker Sorting uses this concept , If you let the element on the left have the same property , Let the left and right elements be sorted first , So the unsorted elements will be concentrated in the middle , Because the left and right sides are sorted at the same time , The unsorted parts in the middle will be reduced quickly . The method lies in two-way bubble sorting , Let's sort the bubbles from left to right , Let's sort the bubbles from right to left , This completes the action of sorting , And you must use left And right Two flags are used to record the positions of the sorted elements at the left and right ends .
An example of sorting is shown below :
Before ordering :45 19 77 81 13 28 18 19 77 11
Sort right :19 45 77 13 28 18 19 77 11 [81]
Sort left :[11] 19 45 77 13 28 18 19 77 [81]
Sort right :[11] 19 45 13 28 18 19 [77 77 81]
Sort left :[11 13] 19 45 18 28 19 [77 77 81]
Sort right :[11 13] 19 18 28 19 [45 77 77 81]
Sort left :[11 13 18] 19 19 28 [45 77 77 81]
Sort right :[11 13 18] 19 19 [28 45 77 77 81]
Sort left :[11 13 18 19 19] [28 45 77 77 81]
As shown above , The brackets indicate the sorted parts on the left and right sides , When left > right when , Then the sorting is finished .
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#define MAX 10
#define SWAP(x,y) {
int t; t = x; x = y; y = t;}
void shakersort(int[]);
int main(void) {
int number[MAX] = {
0};
int i;
srand(time(NULL));
16. Sequencing - Improved selection sorting
explain
The concept of selective sorting is simple , Select a minimum value from the unordered portion each time , Insert the back end of the sorted part , Its time is mainly spent looking for the minimum value in the whole unordered part , If we can speed up the search for the minimum , The rate at which sorting is selected is also
You can speed up ,Heap The sorting method makes the search path from the root to the last leaf , Not the whole unordered part , So it is called the improved selective sorting method .
solution
Heap The sorting method uses Heap Tree( Pile up trees ), A tree is a data structure , The stacked tree is a binary tree , That is, each parent node has at most two child nodes ( For a detailed definition of trees, see the data structure book ), If the parent node of the stacked tree is smaller than the child node , It is called minimum accumulation (Min Heap), If the parent node is larger than the child node , It is called maximum accumulation (Max
Heap), The child nodes of the same layer do not need to care about their size relationship , For example, the following is a stacked tree :
You can use a one-dimensional array to store all the elements of a stacked tree and their order , For the sake of calculation , The starting index used is 1 instead of 0, Indexes 1 Is the root of the tree , If the index of the left child node stored in the array is s, Then the index of its parent node is s/2, The right child node is s+1, As shown above , After converting the stacked tree in the above figure to a one-dimensional array, the following is shown :
First you must know how to build a stacked tree , The elements added to the stacked tree will be placed at the last leaf node first , Then check
Check whether the parent node is smaller than the child node ( Minimum accumulation ), Constantly swap small elements with parent nodes , Until the condition of stacked tree is satisfied
until , For example, add an element to the stack in the figure above 12, The adjustment method of the stack tree is as follows :
After building the stacked tree , The tree root must be the minimum of all elements , Your goal is :
Take out the minimum value and adjust the tree to a stacked tree
Repeat the above steps , You can achieve the effect of sorting , The way to get the minimum value is to exchange the tree root with the last leaf node , Then cut off the leaf nodes , Readjust the tree to a stacked tree , As shown below :
After adjustment , The root node of the tree is the minimum again , So we can repeat this step , Then take the minimum value , And adjust the tree to a stacked tree , As shown below :
After repeating the steps like this , Because of the use of one-dimensional arrays to store stacked trees , Every time the leaves and roots are exchanged, the minimum value is placed in the back-end array , So finally, the array is in the sorted state . In fact, it is accumulated in the process of adjustment , Is an act of choice , Select the minimum value to the tree root each time , Not all the elements are selected , But the path from the roots to the leaves , Thus, the selection process can be accelerated , therefore Heap The sorting method will be called the improved selective sorting method .
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#define MAX 10
#define SWAP(x,y) {
int t; t = x; x = y; y = t;}
void createheap(int[]);
void heapsort(int[]);
int main(void) {
int number[MAX+1] = {
-1};
int i, num;
srand(time(NULL));
printf(" Before ordering :");
for(i = 1; i <= MAX; i++) {
number[i] = rand() % 100;
printf("%d ", number[i]);
}
printf("\n Build a stacked tree :");
createheap(number);
for(i = 1; i <= MAX; i++)
printf("%d ", number[i]);
printf("\n");
heapsort(number);
printf("\n");
return 0;
}
void createheap(int number[]) {
int i, s, p;
int heap[MAX+1] = {
-1};
for(i = 1; i <= MAX; i++) {
heap[i] = number[i];
s = i;
p = i / 2;
while(s >= 2 && heap[p] > heap[s]) {
SWAP(heap[p], heap[s]);
s = p;
p = s / 2;
}
}
for(i = 1; i <= MAX; i++)
number[i] = heap[i];
}
void heapsort(int number[]) {
int i, m, p, s;
m = MAX;
while(m > 1) {
SWAP(number[1], number[m]);
m--;
p = 1;
s = 2 * p;
while(s <= m) {
if(s < m && number[s+1] < number[s])
s++;
if(number[p] <= number[s])
break;
SWAP(number[p], number[s]);
p = s;
s = 2 * p;
}
printf("\n Sorting :");
for(i = MAX; i > 0; i--)
printf("%d ", number[i]);
}
}
17. Quick sort ( One )
explain
Quick sort (quick sort) Is currently recognized as one of the fastest sorting methods ( Depending on the object of the problem ), Although the quick sort method can reach... In the worst case O(n2), But in most cases , The efficiency performance of quick sorting method is quite good . The basic spirit of quick sequencing is to find the appropriate axis in the sequence , Then divide the sequence into two , Sort the left and right series respectively , It is the choice of axis that affects the efficiency of quick sorting . The first version of quicksort introduced here , It is the version mentioned in most textbooks , Because it's the easiest to understand , It is also most in line with the concept of axis segmentation and left-right sorting , Suitable for beginners to explain .
solution
The quick calculation introduced here is as follows : Set the leftmost number to the axis , And record the value as s
Loop handling :
- Order index i Look from the left to the right of the sequence , Until greater than is found s Number of numbers
- Order index j Look from the left and right of the sequence to the left , Until we find less than s Number of numbers
- If i >= j, Then leave the loop
- If i < j, Then exchange the index i And j The value of two places
- Align the left-hand shaft with j swapping
- Recurs the left side of the axis
- Recurs the right side of the axis
Through the following algorithm , Then the values on the left side of the axis will be less than s, The values on the right side of the axis will be greater than s, In this way, the left and right sides of the shaft are recursively , You can complete the purpose of sorting , For example, the following example , Represents the number to be exchanged ,[] Represents the axis :
[41] 24 76 11 45 64 21 69 19 36*
[41] 24 36 11 45* 64 21 69 19* 76
[41] 24 36 11 19 64* 21* 69 45 76
[41] 24 36 11 19 21 64 69 45 76
21 24 36 11 19 [41] 64 69 45 76
In the example above ,41 The values on the left are smaller than it , And the values on the right are larger than that , In this way, you can go back to sorting completion .
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#define MAX 10
#define SWAP(x,y) {
int t; t = x; x = y; y = t;}
void quicksort(int[], int, int);
int main(void) {
int number[MAX] = {
0};
int i, num;
srand(time(NULL));
printf(" Before ordering :");
for(i = 0; i < MAX; i++) {
number[i] = rand() % 100;
printf("%d ", number[i]);
}
quicksort(number, 0, MAX-1);
printf("\n After ordering :");
for(i = 0; i < MAX; i++)
printf("%d ", number[i]);
printf("\n");
return 0;
}
void quicksort(int number[], int left, int right) {
int i, j, s;
if(left < right) {
s = number[left];
i = left;
j = right + 1;
while(1) {
// Look right
while(i + 1 < number.length && number[++i] < s) ;
// Look left
while(j -1 > -1 && number[--j] > s) ;
if(i >= j)
break;
SWAP(number[i], number[j]);
}
number[left] = number[j];
number[j] = s;
quicksort(number, left, j-1); // Recurs to the left
quicksort(number, j+1, right); // Recurs to the right
}
}
18. Quick sort ( Two )
explain
In quick sort ( One ) in , Set the leftmost element as the axis each time , And I have said before , The acceleration of the quick sort method lies in the selection of axes , In this case , Only set the axis to the middle element , Compare against this element , This can increase the efficiency of quick sort .
solution
In this case , Take the middle element s The comparison , In the same way, you have to find the right one first s Big index i, Then compare s Small index j, As long as the indexes on both sides have not intersected , Just exchange i And j The element value of , This time there is no need to exchange the axes , Because in the process of looking for an exchange , The elements of the axis position will also participate in the exchange action , for example :
41 24 76 11 45 64 21 69 19 36
First left by 0,right by 9,(left+right)/2 = 4( Take the quotient of an integer ), So the axis is the index 4 The location of , The elements to compare are 45, You look to the right 45 Big , Look to the left 45 Exchange small ones :
41 24 76* 11 [45] 64 21 69 19 36
41 24 36 11 45 64 21 69 19* 76
41 24 36 11 19 64* 21* 69 45 76
[41 24 36 11 19 21] [64 69 45 76]
After that , At the beginning, do not return the left bracket and the right bracket , In this way, you can accomplish the purpose of sorting .
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#define MAX 10
#define SWAP(x,y) {
int t; t = x; x = y; y = t;}
void quicksort(int[], int, int);
int main(void) {
int number[MAX] = {
0};
int i, num;
srand(time(NULL));
printf(" Before ordering :");
for(i = 0; i < MAX; i++) {
number[i] = rand() % 100;
printf("%d ", number[i]);
}
quicksort(number, 0, MAX-1);
printf("\n After ordering :");
for(i = 0; i < MAX; i++)
printf("%d ", number[i]);
printf("\n");
return 0;
}
void quicksort(int number[], int left, int right) {
int i, j, s;
if(left < right) {
s = number[(left+right)/2];
i = left - 1;
j = right + 1;
while(1) {
while(number[++i] < s) ; // Look right
while(number[--j] > s) ; // Look left
if(i >= j)
break;
SWAP(number[i], number[j]);
}
quicksort(number, left, i-1); // Recurs to the left
quicksort(number, j+1, right); // Recurs to the right
}
}
19. Quick sort ( 3、 ... and )
explain
As I said before, the selection of axes is one of the keys to the efficiency of the quick sort method , The axis selection method of the quick sort method here makes the quick sort method more efficient , It is from the algorithm book Introduction to Algorithms In .
solution
Let's first explain the concept of this quick sort method , It takes the rightmost value s Criteria for comparison , Divide the whole sequence into three parts , One is less than s Part of , One is greater than s Part of , One is the untreated part , As shown below :
In the sort process ,i And j Will continue to compare and exchange to the right , The last sequence will change to the following state :
And then s The value of is placed in the middle , The next step is to sort the left and right columns in the same way , As shown below :
And then s The value of is placed in the middle , The next step is to sort the left and right columns in the same way , As shown below :
The whole process of calculation , Directly extract the virtual code in the book for explanation :
QUICKSORT(A, p, r)
if p < r
then q <- PARTITION(A, p, r)
QUICKSORT(A, p, q-1)
QUICKSORT(A, q+1, r)
end QUICKSORT
PARTITION(A, p, r)
x <- A[r]
i <- p-1
for j <- p to r-1
do if A[j] <= x
then i <- i+1
exchange A[i]<->A[j]
exchange A[i+1]<->A[r]
return i+1
end PARTITION
The calculation of a practical example is as follows :
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#define MAX 10
#define SWAP(x,y) {
int t; t = x; x = y; y = t;}
int partition(int[], int, int);
void quicksort(int[], int, int);
int main(void) {
int number[MAX] = {
0};
int i, num;
srand(time(NULL));
printf(" Before ordering :");
for(i = 0; i < MAX; i++) {
number[i] = rand() % 100;
printf("%d ", number[i]);
}
quicksort(number, 0, MAX-1);
printf("\n After ordering :");
for(i = 0; i < MAX; i++)
printf("%d ", number[i]);
printf("\n");
return 0;
}
int partition(int number[], int left, int right) {
int i, j, s;
s = number[right];
i = left - 1;
for(j = left; j < right; j++) {
if(number[j] <= s) {
i++;
SWAP(number[i], number[j]);
}
}
SWAP(number[i+1], number[right]);
return i+1;
}
void quicksort(int number[], int left, int right) {
int q;
if(left < right) {
q = partition(number, left, right);
quicksort(number, left, q-1);
quicksort(number, q+1, right);
}
}
20. Multi dimensional matrix to one dimensional matrix
explain
sometimes , For the convenience of calculation or data storage space , Using a one-dimensional array is more convenient than a two-dimensional or multi-dimensional array , For example, upper triangular matrix 、 Lower triangular matrix or diagonal matrix , Using a one-dimensional array will save space than using a two-dimensional array .
solution
Take 2D array to 1D array as an example , The index value is defined by 0 Start , When changing from two-dimensional array to one-dimensional array , We have two ways :「 In columns (Row) Mainly 」 or 「 In order to (Column) Mainly 」. because C/C++、Java And so on
Mainly columns , So you may be familiar with the former (Fortran The memory configuration of is based on behavior ). When a two-dimensional array dominated by columns is to be converted to a one-dimensional array , Is to read the two-dimensional array from the top to the next column into the one-dimensional array , At this point, the corresponding formula of the index is as follows , among row And column Is a two-dimensional array index ,loc Represents the corresponding one-dimensional array index :loc = column + row The number of rows is when the main two-dimensional array is to be converted to a one-dimensional array , Is to read a two-dimensional array from left to right into a one-dimensional array , At this point, the corresponding formula of the index is as follows :
loc = row + column The derivation of the column number formula can be seen by drawing a picture , If it is a 3D array , Then the formula is as follows , among i( Number u1)、j( Number u2)、k( Number u3) Represent three indexes of the 3D array respectively :
Mainly columns :loc = iu2u3 + ju3 + k
Act as the Lord :loc = ku1u2 + ju1 + i
The higher dimensions can follow this analogy , However, other data structures are usually recommended for higher dimensions ( For example, object packaging ) Quite specific , It is not easy to make mistakes . stay C/C++ If indicators are used in , I will encounter the problem of index operation and memory space address processing , This is also the formula used here , However, each item must be multiplied by the memory size of the data type .
#include <stdio.h>
#include <stdlib.h>
int main(void) {
int arr1[3][4] = {
{
1, 2, 3, 4},
{
5, 6, 7, 8},
{
9, 10, 11, 12}};
int arr2[12] = {
0};
int row, column, i;
printf(" Original 2D data :\n");
for(row = 0; row < 3; row++) {
for(column = 0; column < 4; column++) {
printf("%4d", arr1[row][column]);
}
printf("\n");
}
printf("\n Mainly columns :");
for(row = 0; row < 3; row++) {
for(column = 0; column < 4; column++) {
i = column + row * 4;
arr2[i] = arr1[row][column];
}
}
for(i = 0; i < 12; i++)
printf("%d ", arr2[i]);
printf("\n Act as the Lord :");
for(row = 0; row < 3; row++) {
for(column = 0; column < 4; column++) {
i = row + column * 3;
arr2[i] = arr1[row][column];
}
}
for(i = 0; i < 12; i++)
printf("%d ", arr2[i]);
printf("\n");
return 0;
}
21. Upper triangle 、 Lower triangle 、 Symmetric matrix
explain
The upper triangular matrix means that the elements of the matrix below the diagonal are 0, namely Aij = 0,i > j, for example :
1 2 3 4 5
0 6 7 8 9
0 0 10 11 12
0 0 0 13 14
0 0 0 0 15
The lower triangular matrix is a matrix whose elements above the diagonal are 0, namely Aij = 0,i < j, for example :
1 0 0 0 0
2 6 0 0 0
3 7 10 0 0
4 8 11 13 0
5 9 12 14 15
A symmetric matrix is a matrix whose elements are symmetric to the diagonal , for example :
1 2 3 4 5
2 6 7 8 9
3 7 10 11 12
4 8 11 13 14
5 9 12 14 15
Most elements of the upper triangular or lower triangular matrix do not store values ( by 0), We can save storage space by using one-dimensional array , And the symmetric matrix is symmetric to the diagonal , So it can be regarded as upper triangle or lower triangle matrix to store .
solution
Suppose the matrix is nxn, For the sake of calculation , We let the array index consist of 1 Start , The upper triangular matrix is transformed into a one-dimensional array , If it is mainly column , The formula is :loc = n*(i-1) - i*(i-1)/2 + j Turn to behavior , The formula is :loc = j*(j-1)/2 + i The lower triangular matrix is transformed into a one-dimensional array , If it is mainly column , The formula is :loc = i*(i-1)/2 + j If behavior is the main , The formula is :loc = n*(j-1) - j*(j-1)/2 + i The derivation of the formula is actually obtained from the formula of the series of equal difference , You can draw by yourself and look at it to prove it , about C/C++ or Java And so on 0 In the beginning language , As long as i And j Gejia 1, Get loc After subtraction 1 You can apply the above formula .
#include <stdio.h>
#include <stdlib.h>
#define N 5
int main(void) {
int arr1[N][N] = {
{
1, 2, 3, 4, 5},
{
0, 6, 7, 8, 9},
{
0, 0, 10, 11, 12},
{
0, 0, 0, 13, 14},
{
0, 0, 0, 0, 15}};
int arr2[N*(1+N)/2] = {
0};
int i, j, loc = 0;
printf(" Original 2D data :\n");
for(i = 0; i < N; i++) {
for(j = 0; j < N; j++) {
printf("%4d", arr1[i][j]);
}
printf("\n");
}
printf("\n Mainly columns :");
for(i = 0; i < N; i++) {
for(j = 0; j < N; j++) {
if(arr1[i][j] != 0)
arr2[loc++] = arr1[i][j];
}
}
for(i = 0; i < N*(1+N)/2; i++)
printf("%d ", arr2[i]);
printf("\n Enter the index (i, j):");
scanf("%d, %d", &i, &j);
loc = N*i - i*(i+1)/2 + j;
printf("(%d, %d) = %d", i, j, arr2[loc]);
printf("\n");
return 0;
}
22.m Elements of the collection n A subset of elements
explain
Suppose a set has m Elements , Arbitrarily take out from the set n Elements , Then this n What are the possible subsets of elements ?
solution
Suppose there is 5 A set point of two elements , Take out 3 The possible subsets of elements are as follows :
{1 2 3}、{1 2 4 }、{1 2 5}、{1 3 4}、{1 3 5}、{1 4 5}、{2 3 4}、{2 3 5}、{2 4 5}、{3 4 5}
These subsets have been arranged in dictionary order , In this way, some rules can be observed :
- If the rightmost element is less than m, Just like the code table, it keeps adding 1
- If the right digit has reached the maximum value , Then add 1 Move to the left
- Every time add 1 Move the position of to the left , The elements on the right must be readjusted to the descending order
So the key point is which position must be added 1 The action of , What is the rightmost position to add 1? Or other places ? When actually writing a program , You can use a variable positon To record the addition of 1 The location of ,position Set as the initial value of n-1, Because we want to use arrays , The rightmost index value is the largest n-1, stay position If the value of the position is less than m Just keep adding 1, If it is greater than m 了 ,position Will decrease 1, That is to move one position to the left ; As the position moves to the left , The elements on the right will be adjusted , So we have to check if the rightmost element is less than m, If it is , be position Adjust back n-1, If not , be positon Remain unchanged .
#include <stdio.h>
#include <stdlib.h>
#define MAX 20
int main(void) {
int set[MAX];
int m, n, position;
int i;
printf(" Enter the number of sets m:");
scanf("%d", &m);
printf(" Input fetch element n:");
scanf("%d", &n);
for(i = 0; i < n; i++)
set[i] = i + 1;
// Show the first set
for(i = 0; i < n; i++)
printf("%d ", set[i]);
putchar('\n');
position = n - 1;
while(1) {
if(set[n-1] == m)
position--;
else
position = n - 1;
set[position]++;
// Adjust the right element
for(i = position + 1; i < n; i++)
set[i] = set[i-1] + 1;
for(i = 0; i < n; i++)
printf("%d ", set[i]);
putchar('\n');
if(set[0] >= m - n + 1)
break;
}
return 0;
}
23. Digital disassembly
explain
This topic comes from digital disassembly , I'll change it to C Language version , And add a description .
The title is like this :
3 = 2+1 = 1+1+1 therefore 3 There are three ways to disassemble
4 = 3 + 1 = 2 + 2 = 2 + 1 + 1 = 1 + 1 + 1 + 1 Five kinds in total
5 = 4 + 1 = 3 + 2 = 3 + 1 + 1 = 2 + 2 + 1 = 2 + 1 + 1 + 1 = 1 + 1 +1 +1 +1
There are seven, and so on , May I have a specific number NUM How many disassembly methods are there ?
solution
Our last number in the above example 5 As an example , hypothesis f( n ) Is the number n The number of detachable ways , and f(x, y) For the use of y The following figures are used to disassemble x The number of methods used , Observe :
5 = 4 + 1 = 3 + 2 = 3 + 1 + 1 = 2 + 2 + 1 = 2 + 1 + 1 + 1 = 1 + 1 +1 +1 +1
If you use a function to express :
f(5) = f(4, 1) + f(3,2) + f(2,3) + f(1,4) + f(0,5)
among f(1, 4) = f(1, 3) + f(1, 2) + f(1, 1), But use greater than 1 To disassemble 1 It makes no sense , therefore f(1, 4) =f(1, 1), And the same ,f(0, 5) It will be equal to f(0, 0), therefore :
f(5) = f(4, 1) + f(3,2) + f(2,3) + f(1,1) + f(0,0)
Follow the instructions above , Use dynamic programming (Dynamic programming) To solve it , among f(4,1) In fact, that is f(5-1, min(5-1,1)),f(x, y) Is equal to f(n-y, min(n-x, y)), among n For the number to be disassembled , and min() Means take two
The smaller of the two . Use a 2D array table table[x][y] To express f(x, y), At the beginning , Index each column 0 And index 1 The element value is set to 1, Because any number 0 The following number must be only 1 Kind of , And any number 1 The following numbers must be only 1 Kind of :
for(i = 0; i < NUM +1; i++){
table[i][0] = 1; // Any number 0 The following number must be only 1 Kind of
table[i][1] = 1; // Any number 1 The following number must be only 1 Kind of
} Next, we will start to disassemble one by one , If the number is NUM, Then our array dimension size must be NUM x
(NUM/2+1), In numbers 10 For example , Its dimension is 10 x 6 Our table will look like this :
1 1 0 0 0 0
1 1 0 0 0 0
1 1 2 0 0 0
1 1 2 3 0 0
1 1 3 4 5 0
1 1 3 5 6 7
1 1 4 7 9 0
1 1 4 8 0 0
1 1 5 0 0 0
1 1 0 0 0 0
#include <stdio.h>
#include <stdlib.h>
#define NUM 10 // The number to be disassembled
#define DEBUG 0
int main(void) {
int table[NUM][NUM/2+1] = {
0}; // Dynamic planning tables
int count = 0;
int result = 0;
int i, j, k;
printf(" Digital disassembly \n");
printf("3 = 2+1 = 1+1+1 therefore 3 There are three ways to disassemble \n");
printf("4 = 3 + 1 = 2 + 2 = 2 + 1 + 1 = 1 + 1 + 1 + 1");
printf(" Five kinds in total \n");
printf("5 = 4 + 1 = 3 + 2 = 3 + 1 + 1");
printf(" = 2 + 2 + 1 = 2 + 1 + 1 + 1 = 1 + 1 +1 +1 +1");
printf(" There are seven kinds of \n");
printf(" And so on , seek %d There are several ways to disassemble ?", NUM);
// initialization
for(i = 0; i < NUM; i++){
table[i][0] = 1; // Any number 0 The following number must be only 1 Kind of
table[i][1] = 1; // Any number 1 The following number must be only 1 Kind of
}
// Dynamic programming
for(i = 2; i <= NUM; i++){
for(j = 2; j <= i; j++){
if(i + j > NUM) // Greater than NUM
continue;
count = 0;
for(k = 1 ; k <= j; k++){
count += table[i-k][(i-k >= k) ? k : i-k];
}
table[i][j] = count;
}
}
// Calculate and display results
for(k = 1 ; k <= NUM; k++)
result += table[NUM-k][(NUM-k >= k) ? k : NUM-k];
printf("\n\nresult: %d\n", result);
if(DEBUG) {
printf("\n Debug information \n");
for(i = 0; i < NUM; i++) {
for(j = 0; j < NUM/2+1; j++)
printf("%2d", table[i][j]);
printf("\n");
}
}
return 0;
}
边栏推荐
- 我如何编码8个小时而不会感到疲倦。
- 蓝桥杯2022年第十三届省赛真题-积木画
- LeetCode:1175. 质数排列
- Reptile practice (VI): novel of climbing pen interesting Pavilion
- C语言实例_2
- 1123. The nearest common ancestor of the deepest leaf node
- 制作带照明的DIY焊接排烟器
- C language instance_ two
- Appium自动化测试基础 — uiautomatorviewer定位工具
- Appium automation test foundation uiautomatorviewer positioning tool
猜你喜欢

454-百度面经1
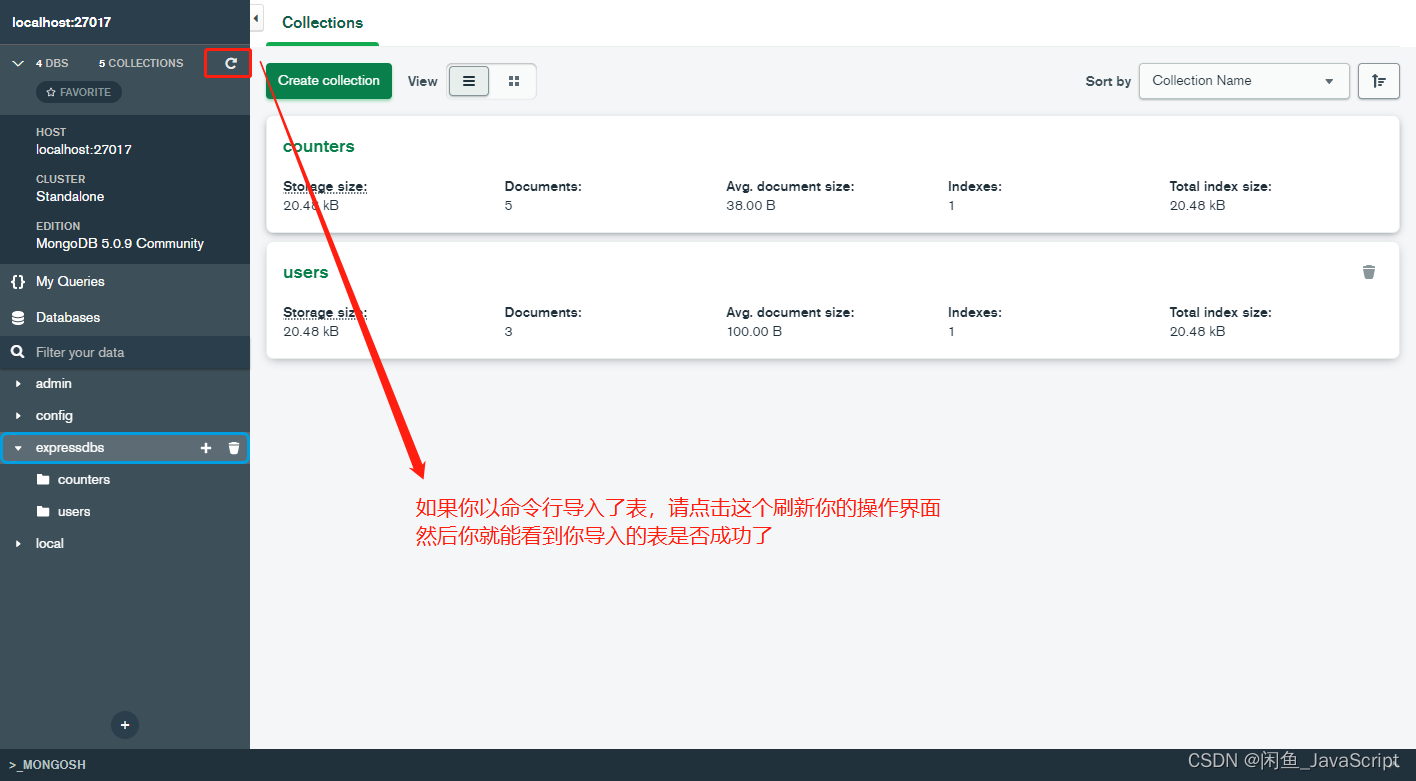
mongodb查看表是否导入成功
Appium自动化测试基础 — uiautomatorviewer定位工具
dvajs的基础介绍及使用
js如何快速创建一个长度为 n 的数组
Comparison of picture beds of free white whoring
盒子拉伸拉扯(左右模式)
Go zero micro service practical series (IX. ultimate optimization of seckill performance)

Appium automation test foundation uiautomatorviewer positioning tool

蓝桥杯2022年第十三届省赛真题-积木画
随机推荐
1123. 最深叶节点的最近公共祖先
移植DAC芯片MCP4725驱动到NUC980
What does security capability mean? What are the protection capabilities of different levels of ISO?
mongodb查看表是否导入成功
域分析工具BloodHound的使用说明
C language instance_ three
Your cache folder contains root-owned files, due to a bug in npm ERR! previous versions of npm which
WCF Foundation
设置Wordpress伪静态连接(无宝塔)
swiper组件中使用video导致全屏错位
搭建【Redis in CentOS7.x】
Dark horse notes - create immutable sets and streams
LeetCode. 剑指offer 62. 圆圈中最后剩下的数
一起看看matlab工具箱内部是如何实现BP神经网络的
Google发布安全更新,修复Chrome中已被利用的0 day
Set up [redis in centos7.x]
对C语言数组的再认识
Appium自动化测试基础 — uiautomatorviewer定位工具
鼠标右键 自定义
[chip scheme design] pulse oximeter