当前位置:网站首页>LeetCode 1584. Minimum cost of connecting all points
LeetCode 1584. Minimum cost of connecting all points
2022-07-06 16:43:00 【Daylight629】
1584. The minimum cost of connecting all points
To give you one points Array , Express 2D Some points on the plane , among points[i] = [xi, yi] .
Connection point [xi, yi] Sum point [xj, yj] The cost is between them Manhattan distance :|xi - xj| + |yi - yj| , among |val| Express val The absolute value of .
Please return the minimum total cost of connecting all points . Just between any two points Yes and no A simple path , All the points are connected .
Example 1:

Input :points = [[0,0],[2,2],[3,10],[5,2],[7,0]]
Output :20
explain :
We can connect all the points as shown in the figure above to get the minimum total cost , The total cost is 20 .
Notice that there is only one path between any two points to reach each other .
Example 2:
Input :points = [[3,12],[-2,5],[-4,1]]
Output :18
Example 3:
Input :points = [[0,0],[1,1],[1,0],[-1,1]]
Output :4
Example 4:
Input :points = [[-1000000,-1000000],[1000000,1000000]]
Output :4000000
Example 5:
Input :points = [[0,0]]
Output :0
Tips :
1 <= points.length <= 1000-106 <= xi, yi <= 106- All points
(xi, yi)Two are different .
Two 、 Method 1
Kruskal Algorithm
class Solution {
public int minCostConnectPoints(int[][] points) {
int n = points.length;
DisjointSetUnion dsu = new DisjointSetUnion(n);
List<Edge> edges = new ArrayList<Edge>();
for (int i = 0; i < n; i++) {
for (int j = i + 1; j < n; j++) {
edges.add(new Edge(dist(points, i, j), i, j));
}
}
Collections.sort(edges, new Comparator<Edge>() {
public int compare(Edge edge1, Edge edge2) {
return edge1.len - edge2.len;
}
});
int ret = 0, num = 1;
for (Edge edge : edges) {
int len = edge.len, x = edge.x, y = edge.y;
if (dsu.unionSet(x, y)) {
ret += len;
num++;
if (num == n) {
break;
}
}
}
return ret;
}
public int dist(int[][] points, int x, int y) {
return Math.abs(points[x][0] - points[y][0]) + Math.abs(points[x][1] - points[y][1]);
}
}
class DisjointSetUnion {
int[] f;
int[] rank;
int n;
public DisjointSetUnion(int n) {
this.n = n;
this.rank = new int[n];
Arrays.fill(this.rank, 1);
this.f = new int[n];
for (int i = 0; i < n; i++) {
this.f[i] = i;
}
}
public int find(int x) {
return f[x] == x ? x : (f[x] = find(f[x]));
}
public boolean unionSet(int x, int y) {
int fx = find(x), fy = find(y);
if (fx == fy) {
return false;
}
if (rank[fx] < rank[fy]) {
int temp = fx;
fx = fy;
fy = temp;
}
rank[fx] += rank[fy];
f[fy] = fx;
return true;
}
}
class Edge {
int len, x, y;
public Edge(int len, int x, int y) {
this.len = len;
this.x = x;
this.y = y;
}
}
Complexity analysis
Time complexity :O(n2 log(n)), among n It's the number of nodes . commonly Kruskal yes O(mlogm) The algorithm of , But in this question m=n^2
, So the total time complexity is O(n2log(n)).Spatial complexity :O(n^2), among n It's the number of nodes . Use of parallel search set O(n) Space , The edge set array needs to use O(n^2) Space .
边栏推荐
- Chapter 6 datanode
- 音视频开发面试题
- SF smart logistics Campus Technology Challenge (no T4)
- Raspberry pie 4B installation opencv3.4.0
- Research Report on market supply and demand and strategy of China's four seasons tent industry
- 视频压缩编码和音频压缩编码基本原理
- Chapter 5 yarn resource scheduler
- QT implementation window gradually disappears qpropertyanimation+ progress bar
- Codeforces Round #771 (Div. 2)
- Codeforces Global Round 19
猜你喜欢
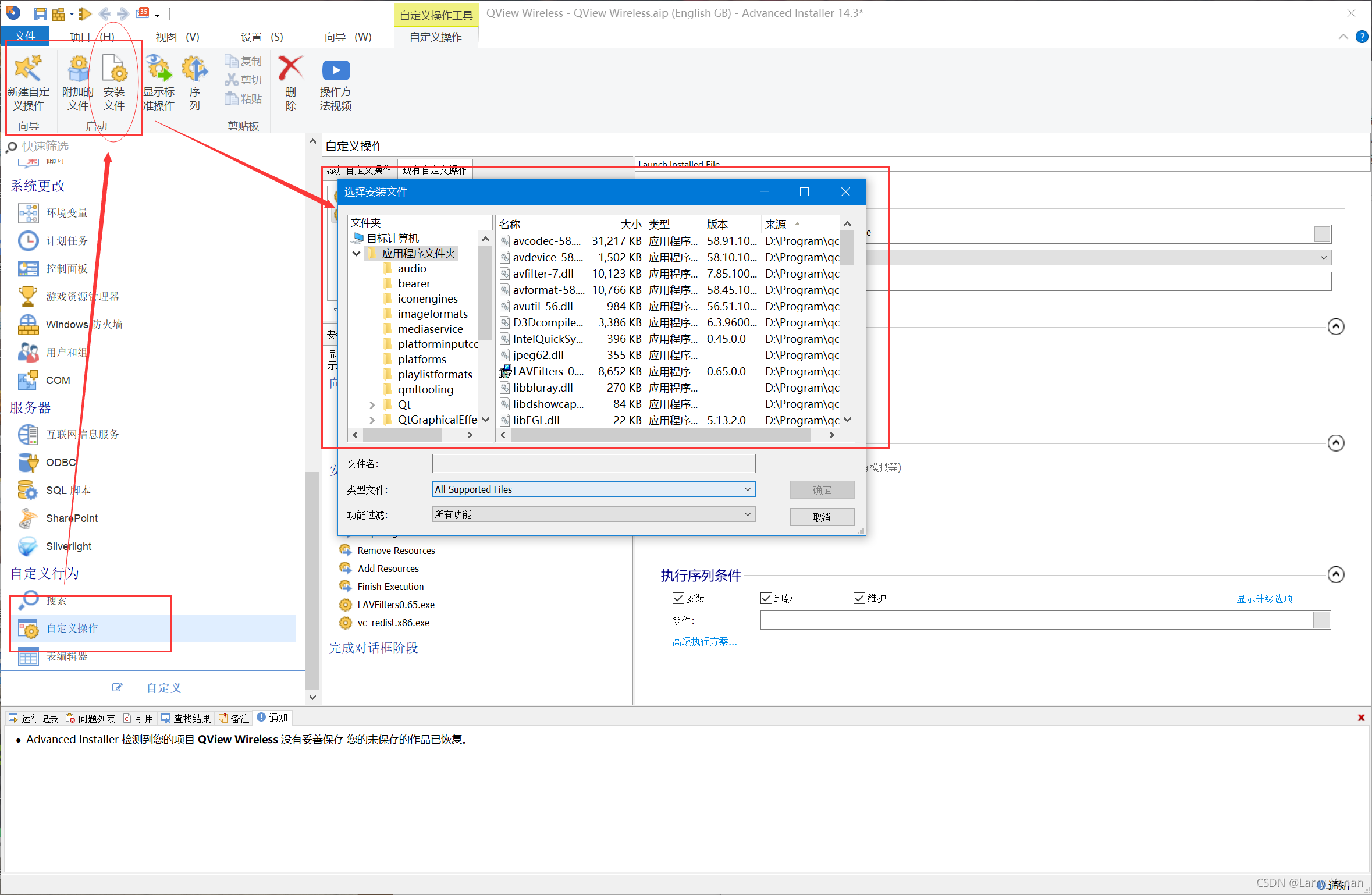
Advancedinstaller installation package custom action open file

antd upload beforeUpload中禁止触发onchange
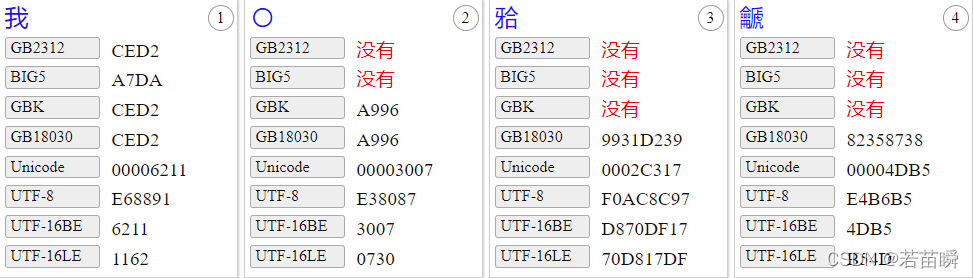
【锟斤拷】的故事:谈谈汉字编码和常用字符集

图像处理一百题(1-10)
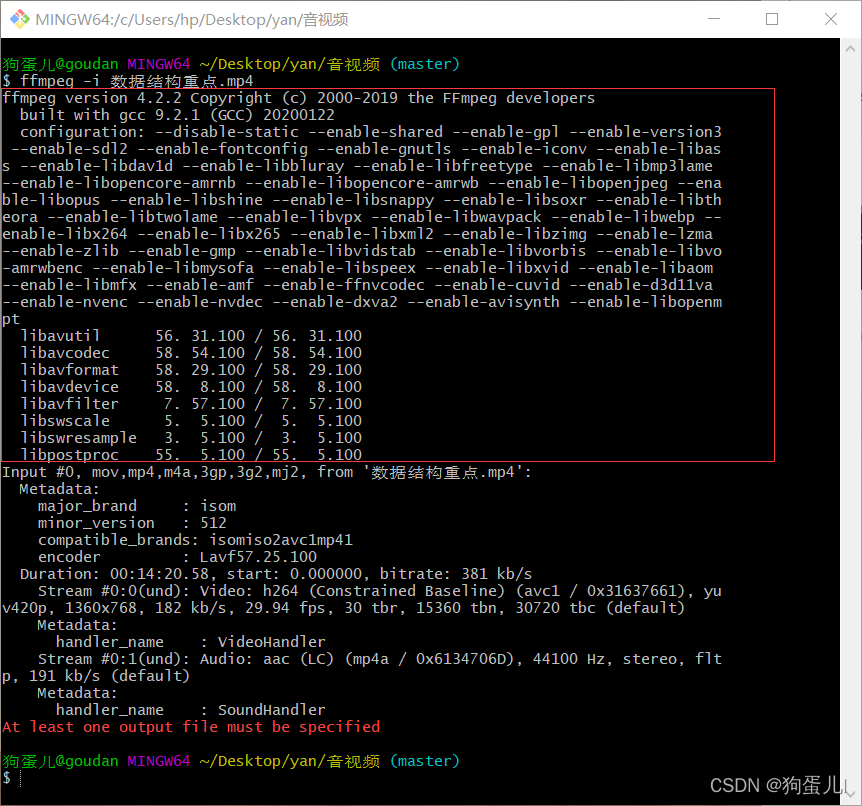
Ffmpeg command line use
Cmake Express

ByteDance new programmer's growth secret: those glittering treasures mentors

第三章 MapReduce框架原理

QT implementation window gradually disappears qpropertyanimation+ progress bar
Local visualization tools are connected to redis of Alibaba cloud CentOS server
随机推荐
Solve the problem that intel12 generation core CPU single thread only runs on small cores
Business system compatible database oracle/postgresql (opengauss) /mysql Trivia
Browser print margin, default / borderless, full 1 page A4
Oneforall installation and use
Raspberry pie 4B installation opencv3.4.0
Research Report of desktop clinical chemical analyzer industry - market status analysis and development prospect prediction
sublime text 代码格式化操作
Hbuilder x format shortcut key settings
CMake速成
Chapter 6 rebalance details
Basic principles of video compression coding and audio compression coding
Spark的RDD(弹性分布式数据集)返回大结果集
js封装数组反转的方法--冯浩的博客
Useeffect, triggered when function components are mounted and unloaded
(lightoj - 1369) answering queries (thinking)
Calculate the time difference
JS encapsulates the method of array inversion -- Feng Hao's blog
Research Report on market supply and demand and strategy of China's four seasons tent industry
LeetCode 1545. Find the k-th bit in the nth binary string
Native JS realizes the functions of all selection and inverse selection -- Feng Hao's blog