当前位置:网站首页>Codeforces Global Round 19
Codeforces Global Round 19
2022-07-06 09:29:00 【狗蛋儿l】
A. Sorting Parts
You have an array a of length n. You can exactly once select an integer len between 1 and n−1 inclusively, and then sort in non-decreasing order the prefix of the array of length len and the suffix of the array of length n−len
For example, if the array is a=[3,1,4,5,2], and you choose len=2, then after that the array will be equal to [1,3,2,4,5].
Could it be that after performing this operation, the array will not be sorted in non-decreasing order?
Input
There are several test cases in the input data. The first line contains a single integer t (1≤t≤100) — the number of test cases. This is followed by the test cases description.
The first line of each test case contains one integer n
(2≤n≤104) — the length of the array.
The second line of the test case contains a sequence of integers a1,a2,…,an (1≤ai≤109) — the array elements.
It is guaranteed that the sum of nover all test cases does not exceed 104.
Output
For each test case of input data, output “YES” (without quotes), if the array may be not sorted in non-decreasing order, output “NO” (without quotes) otherwise. You can output each letter in any case (uppercase or lowercase).
Example
Input
3
3
2 2 1
4
3 1 2 1
5
1 2 2 4 4
Output
YES
YES
NO
Note
In the first test case, it’s possible to select len=1, then after operation, the array will not be sorted in non-decreasing order and will be equal to [2,1,2].
In the second test case, it’s possible to select len=3, then after operation, the array will not be sorted in non-decreasing order and will be equal to [1,2,3,1].
In the third test case, the array will be sorted in non-decreasing order for every possible len.
思路:
大概就是判断这个数组是不是有序,有序就YES,无序就NO
#include <bits/stdc++.h>
using namespace std;
int main() {
int t;
cin >> t;
for (int i = 0; i < t; i++) {
int n;
cin >> n;
vector<int> a(n);
for (auto& u : a)
cin >> u;
if (!is_sorted(a.begin(), a.end()))
cout << "YES\n";
else
cout << "NO\n";
}
}
B. MEX and Array
Let there be an array b1,b2,…,bk. Let there be a partition of this array into segments [l1;r1],[l2;r2],…,[lc;rc], where l1=1, rc=k, and for any 2≤i≤c holds that ri−1+1=li. In other words, each element of the array belongs to exactly one segment.
Let’s define the cost of a partition as c+∑i=1cmex({bli,bli+1,…,bri}),where mex of a set of numbers S is the smallest non-negative integer that does not occur in the set S. In other words, the cost of a partition is the number of segments plus the sum of MEX over all segments. Let’s define the value of an array b1,b2,…,bk as the maximum possible cost over all partitions of this array.You are given an array a of size n. Find the sum of values of all its subsegments.An array x is a subsegment of an array y if x can be obtained from y by deletion of several (possibly, zero or all) elements from the beginning and several (possibly, zero or all) elements from the end.
Input
The input contains several test cases. The first line contains one integer t
(1≤t≤30) — the number of test cases.
The first line for each test case contains one integer n
(1≤n≤100) — the length of the array.
The second line contains a sequence of integers a1,a2,…,an
(0≤ai≤109) — the array elements.
It is guaranteed that the sum of the values n
over all test cases does not exceed 100.
Output
For each test case print a single integer — the answer to the problem.
Example
Input
4
2
1 2
3
2 0 1
4
2 0 5 1
5
0 1 1 0 1
Output
4
14
26
48
#include <bits/stdc++.h>
using namespace std;
int main() {
int t;
cin >> t;
for (int i = 0; i < t; i++) {
int n;
cin >> n;
vector<int> a(n);
for (auto& u : a)
cin >> u;
int ans = 0;
for (int i = 0; i < n; i++) {
ans += (i + 1) * (n - i);
if (a[i] == 0)
ans += (i + 1) * (n - i);
}
cout << ans << '\n';
}
}
C. Andrew and Stones
Andrew has n piles with stones. The i-th pile contains ai stones. He wants to make his table clean so he decided to put every stone either to the 1-st or the n-th pile.
Andrew can perform the following operation any number of times: choose 3 indices 1≤i<j<k≤n, such that the j-th pile contains at least 2 stones, then he takes 2 stones from the pile j and puts one stone into pile i and one stone into pile k.
Tell Andrew what is the minimum number of operations needed to move all the stones to piles 1and n, or determine if it’s impossible.
Input
The input contains several test cases. The first line contains one integer t
(1≤t≤10000) — the number of test cases.
The first line for each test case contains one integer n
(3≤n≤105) — the length of the array.
The second line contains a sequence of integers a1,a2,…,an
(1≤ai≤109) — the array elements.
It is guaranteed that the sum of the values n
over all test cases does not exceed 105.
Output
For each test case print the minimum number of operations needed to move stones to piles 1 and n, or print −1 if it’s impossible.
Input
4
5
1 2 2 3 6
3
1 3 1
3
1 2 1
4
3 1 1 2
Output
4
-1
1
-1
#include <bits/stdc++.h>
using namespace std;
void solve() {
int n;
cin >> n;
vector<int> a(n);
for (auto &x : a)
cin >> x;
if (*max_element(a.begin() + 1, a.end() - 1) == 1 || (n == 3 && a[1] % 2 == 1)) {
cout << "-1\n";
return;
}
long long answer = 0;
for (int i = 1; i < n - 1; i++)
answer += (a[i] + 1) / 2;
cout << answer << '\n';
}
int main() {
ios::sync_with_stdio(false), cin.tie(nullptr);
int tests;
cin >> tests;
while (tests--)
solve();
}
边栏推荐
- (POJ - 3258) River hopper (two points)
- 提交Spark应用的若干问题记录(sparklauncher with cluster deploy mode)
- Codeforces - 1526C1&&C2 - Potions
- Base dice (dynamic programming + matrix fast power)
- 分享一个在树莓派运行dash应用的实例。
- (POJ - 3685) matrix (two sets and two parts)
- QNetworkAccessManager实现ftp功能总结
- window11 conda安装pytorch过程中遇到的一些问题
- Codeforces Round #799 (Div. 4)A~H
- Market trend report, technical innovation and market forecast of tabletop dishwashers in China
猜你喜欢

Browser print margin, default / borderless, full 1 page A4

< li> dot style list style type

QT implementation window gradually disappears qpropertyanimation+ progress bar
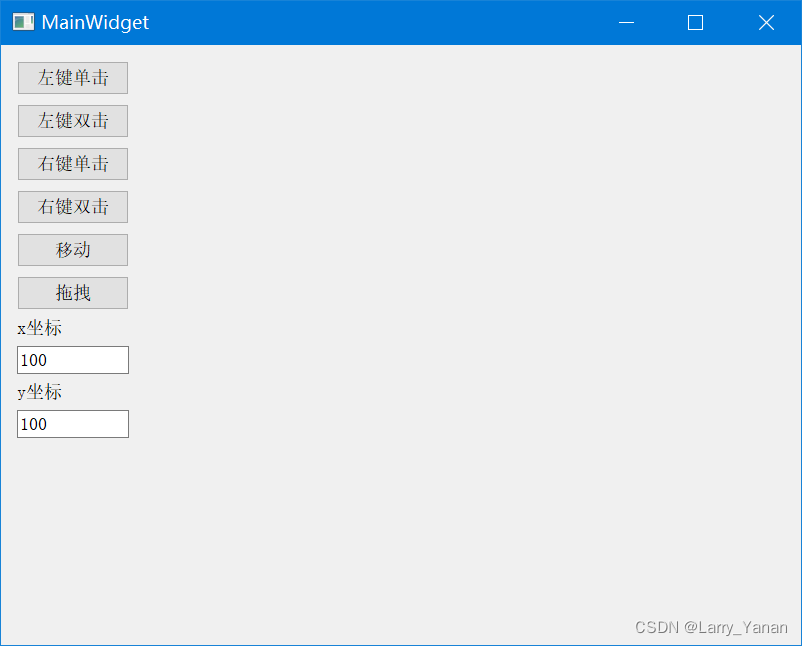
QT模拟鼠标事件,实现点击双击移动拖拽等

业务系统兼容数据库Oracle/PostgreSQL(openGauss)/MySQL的琐事

<li>圆点样式 list-style-type
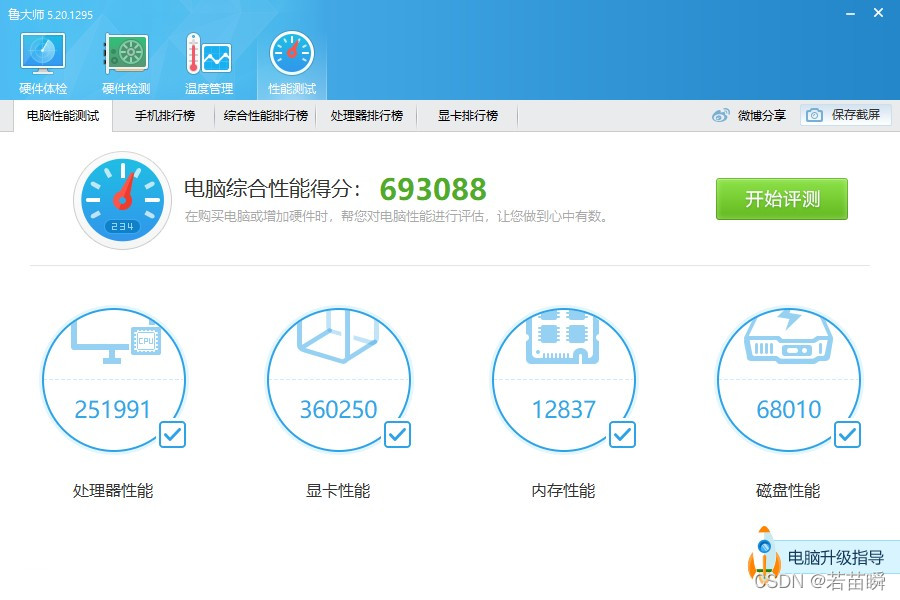
解决Intel12代酷睿CPU【小核载满,大核围观】的问题(WIN11)
Share an example of running dash application in raspberry pie.
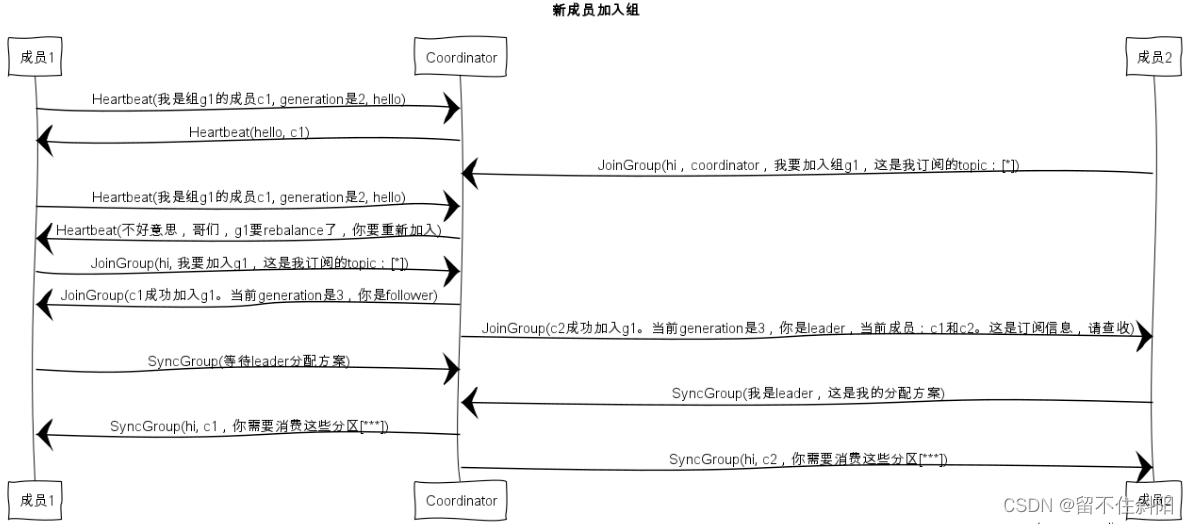
第6章 Rebalance详解

It is forbidden to trigger onchange in antd upload beforeupload
随机推荐
Codeforces Round #800 (Div. 2)AC
Discussion on QWidget code setting style sheet
Effet d'utilisation, déclenché lorsque les composants de la fonction sont montés et déchargés
Click QT button to switch qlineedit focus (including code)
VMware Tools和open-vm-tools的安装与使用:解决虚拟机不全屏和无法传输文件的问题
807. Maintain the urban skyline
Chapter 5 detailed explanation of consumer groups
QT实现圆角窗口
第一章 MapReduce概述
Is the sanic asynchronous framework really so strong? Find truth in practice
Date plus 1 day
(POJ - 3579) median (two points)
AcWing——第55场周赛
Market trend report, technological innovation and market forecast of desktop electric tools in China
Anaconda下安装Jupyter notebook
Acwing: the 56th weekly match
Suffix expression (greed + thinking)
QT simulates mouse events and realizes clicking, double clicking, moving and dragging
Tert butyl hydroquinone (TBHQ) Industry Research Report - market status analysis and development prospect forecast
QT implementation fillet window