当前位置:网站首页>强化学习基础记录
强化学习基础记录
2022-07-06 09:22:00 【喜欢库里的强化小白】
DQN算法是Q-learning算法与深度神经网络的结合(Deep-Q-Network),用于解决维度过高的问题。
一、环境介绍
这里使用的是gym环境的’CartPole-v0’,在这里做简要介绍,详细介绍附上链接。
链接: OpenAI Gym 经典控制环境介绍——CartPole(倒立摆)
(1)游戏规则:游戏里面有一个小车,上有竖着一根杆子,每次重置后的初始状态会有所不同。
<1>杆子倾斜的角度θ不能大于15°
<2>小车移动的位置x需保持在一定范围(中间到两边各2.4个单位长度)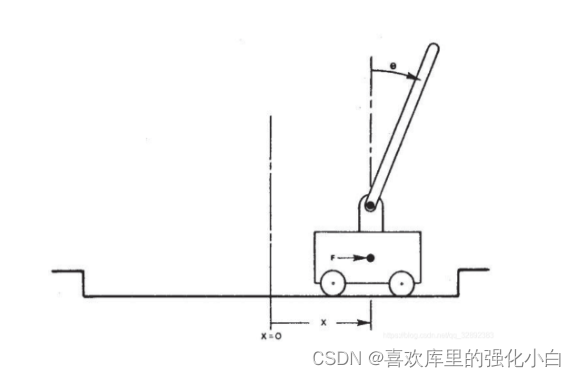
(2)状态空间:这里状态空间是连续的,状态数有4个;
(3)动作空间:这里动作空间是离散的,0代表左移,1代表右移。
(4)奖励:在gym的Cart Pole环境(env)里面,左移或者右移小车的action之后,env会返回一个+1的reward。
二、算法简单介绍
- Value-based
- Off-Policy
- DQN的特点:
<1>神经网络的使用:
当状态动作空间较大或连续时,无法通过Q表形式存储状态-动作价值Q(s,a)。因此可以通过神经网络,拟合状态和价值之间的关系。其中,输入为状态值,输出为每个动作对应的q值。
DQN一般用来解决离散动作空间问题。因为在连续动作空间中,无法通过一一列举动作,去求取对应的q值。如果要解决连续动作空间问题,需要引入AC框架。
<2>经验回放机制的使用:
经验回放就是一种让经验概率分布变得稳定的技术,可以提高训练的稳定性。经验回放主要有“存储”和“回放”两大关键步骤:
经验存储: 每一步,智能体会存储一个(s,a,r,s_,done)的轨迹,也叫transition,将该条记录存入经验池。
经验回放:在程序实现中,当存储的经验大于设定值后,便可以在经验池中,等概率的抽取BATCH_SIZE条经验进行训练,这打破了数据间的关联,同时重复利用经验,也提高了数据的利用率。在实际问题中,可能根据经验的重要程度,进行依据权重的优先回放。
<3>目标网络的使用:
链接: 目标网络
简单来说,DQN中引入了两个网络,一个是行为网络,一个是目标网络,二者结构和参数相同,只是参数存在滞后性,每隔一段时间,对目标网络进行一次更新。这里的更新可以进行硬更新,将参数直接喂过去,也可以进行软更新,通过权重更新。这种滞后更新,也稳定了Q网络的学习。
其中目标网络不进行反向传递,相当于一个参照,行为网络通过训练,进行反向传播,越接近目标网络,说明对Q值的评估更准确。 - 伪代码

- 实现
链接: 莫烦
参考了莫烦的实现,其中有的地方,不太理解,加了注释。
import matplotlib.pyplot as plt
import torch # 导入torch
import torch.nn as nn # 导入torch.nn
import torch.nn.functional as F # 导入torch.nn.functional
import numpy as np # 导入numpy
import gym # 导入gym
# 超参数
BATCH_SIZE = 32 # 样本数量
LR = 0.01 # 学习率
EPSILON = 0.9 # greedy policy
GAMMA = 0.9 # reward discount
TARGET_REPLACE_ITER = 100 # 目标网络更新频率
MEMORY_CAPACITY = 2000 # 记忆库容量
env = gym.make('CartPole-v0').unwrapped # 使用gym库中的环境:CartPole,且打开封装(若想了解该环境,请自行百度)
N_ACTIONS = env.action_space.n # 杆子动作个数 (2个)
N_STATES = env.observation_space.shape[0] # 杆子状态个数 (4个)
""" torch.nn是专门为神经网络设计的模块化接口。nn构建于Autograd之上,可以用来定义和运行神经网络。 nn.Module是nn中十分重要的类,包含网络各层的定义及forward方法。 定义网络: 需要继承nn.Module类,并实现forward方法。 一般把网络中具有可学习参数的层放在构造函数__init__()中。 只要在nn.Module的子类中定义了forward函数,backward函数就会被自动实现(利用Autograd)。 """
# 定义Net类 (定义网络)
class Net(nn.Module):
def __init__(self): # 定义Net的一系列属性
# nn.Module的子类函数必须在构造函数中执行父类的构造函数
super(Net, self).__init__() # 等价与nn.Module.__init__()
self.fc1 = nn.Linear(N_STATES, 50) # 设置第一个全连接层(输入层到隐藏层): 状态数个神经元到50个神经元
self.fc1.weight.data.normal_(0, 0.1) # 权重初始化 (均值为0,方差为0.1的正态分布)
self.out = nn.Linear(50, N_ACTIONS) # 设置第二个全连接层(隐藏层到输出层): 50个神经元到动作数个神经元
self.out.weight.data.normal_(0, 0.1) # 权重初始化 (均值为0,方差为0.1的正态分布)
def forward(self, x): # 定义forward函数 (x为状态)
x = F.relu(self.fc1(x)) # 连接输入层到隐藏层,且使用激励函数ReLU来处理经过隐藏层后的值
actions_value = self.out(x) # 连接隐藏层到输出层,获得最终的输出值 (即动作值)
return actions_value # 返回动作值
# 定义DQN类 (定义两个网络)
class DQN(object):
def __init__(self): # 定义DQN的一系列属性
self.eval_net, self.target_net = Net(), Net() # 利用Net创建两个神经网络: 评估网络和目标网络
self.learn_step_counter = 0 # for target updating
self.memory_counter = 0 # for storing memory
self.memory = np.zeros((MEMORY_CAPACITY, N_STATES * 2 + 2)) # 初始化记忆库,一行代表一个transition
self.optimizer = torch.optim.Adam(self.eval_net.parameters(), lr=LR) # 使用Adam优化器 (输入为评估网络的参数和学习率)
self.loss_func = nn.MSELoss() # 使用均方损失函数 (loss(xi, yi)=(xi-yi)^2)
def choose_action(self, x): # 定义动作选择函数 (x为状态)
x = torch.unsqueeze(torch.FloatTensor(x), 0) # 将x转换成32-bit floating point形式,并在dim=0增加维数为1的维度
if np.random.uniform() < EPSILON: # 生成一个在[0, 1)内的随机数,如果小于EPSILON,选择最优动作
actions_value = self.eval_net.forward(x) # 通过对评估网络输入状态x,前向传播获得动作值
#torch.max(a,1)表示选取a中每行最大元素,[1]表示类似键值对的索引 [0]表示把numpy的一维数组取出来
action = torch.max(actions_value, 1)[1].data.numpy() # 输出每一行最大值的索引,并转化为numpy ndarray形式
action = action[0] # 输出action的第一个数
else: # 随机选择动作
action = np.random.randint(0, N_ACTIONS) # 这里action随机等于0或1 (N_ACTIONS = 2)
return action # 返回选择的动作 (0或1)
def store_transition(self, s, a, r, s_): # 定义记忆存储函数 (这里输入为一个transition)
transition = np.hstack((s, [a, r], s_)) # 在水平方向上拼接数组
# 如果记忆库满了,便覆盖旧的数据
index = self.memory_counter % MEMORY_CAPACITY # 获取transition要置入的行数
self.memory[index, :] = transition # 置入transition
self.memory_counter += 1 # memory_counter自加1
def learn(self): # 定义学习函数(记忆库已满后便开始学习)
# 目标网络参数更新
if self.learn_step_counter % TARGET_REPLACE_ITER == 0: # 一开始触发,然后每100步触发
self.target_net.load_state_dict(self.eval_net.state_dict()) # 将评估网络的参数赋给目标网络
self.learn_step_counter += 1 # 学习步数自加1
# 抽取记忆库中的批数据
#sampe_index:ndarray(32,)
sample_index = np.random.choice(MEMORY_CAPACITY, BATCH_SIZE) # 在[0, 2000)内随机抽取32个数,可能会重复
#b_memory:ndarray(32,10) #b_s:ndarray(32,4)
b_memory = self.memory[sample_index, :] # 抽取32个索引对应的32个transition,存入b_memory
b_s = torch.FloatTensor(b_memory[:, :N_STATES])
# 将32个s抽出,转为32-bit floating point形式,并存储到b_s中,b_s为32行4列
b_a = torch.LongTensor(b_memory[:, N_STATES:N_STATES+1].astype(int))
# 将32个a抽出,转为64-bit integer (signed)形式,并存储到b_a中 (之所以为LongTensor类型,是为了方便后面torch.gather的使用),b_a为32行1列
b_r = torch.FloatTensor(b_memory[:, N_STATES+1:N_STATES+2])
# 将32个r抽出,转为32-bit floating point形式,并存储到b_s中,b_r为32行1列
b_s_ = torch.FloatTensor(b_memory[:, -N_STATES:])
# 将32个s_抽出,转为32-bit floating point形式,并存储到b_s中,b_s_为32行4列
# 获取32个transition的评估值和目标值,并利用损失函数和优化器进行评估网络参数更新
q_eval1 = self.eval_net(b_s)
q_eval = q_eval1.gather(1, b_a)
# eval_net(b_s)通过评估网络输出32行每个b_s对应的一系列动作值,然后.gather(1, b_a)代表对每行对应索引b_a的Q值提取进行聚合
q_next = self.target_net(b_s_).detach()
# q_next不进行反向传递误差,所以detach;q_next表示通过目标网络输出32行每个b_s_对应的一系列动作值
q = q_next.max(1)[0]
q_target = b_r + GAMMA * q.view(BATCH_SIZE,1)
# q_next.max(1)[0]表示只返回每一行的最大值,不返回索引(长度为32的一维张量);.view()表示把前面所得到的一维张量变成(BATCH_SIZE, 1)的形状;最终通过公式得到目标值
loss = self.loss_func(q_eval, q_target)
# 输入32个评估值和32个目标值,使用均方损失函数
self.optimizer.zero_grad() # 清空上一步的残余更新参数值
loss.backward() # 误差反向传播, 计算参数更新值
self.optimizer.step() # 更新评估网络的所有参数
dqn = DQN() # 令dqn=DQN类
rewards = []
for i in range(400): # 400个episode循环
print('<<<<<<<<<Episode: %s' % i)
s = env.reset() # 重置环境
episode_reward_sum = 0 # 初始化该循环对应的episode的总奖励
while True: # 开始一个episode (每一个循环代表一步)
env.render() # 显示实验动画
a = dqn.choose_action(s) # 输入该步对应的状态s,选择动作
s_, r, done, info = env.step(a) # 执行动作,获得反馈
#修改奖励 (不修改也可以,修改奖励只是为了更快地得到训练好的摆杆)
x, x_dot, theta, theta_dot = s_
r1 = (env.x_threshold - abs(x)) / env.x_threshold - 0.8
r2 = (env.theta_threshold_radians - abs(theta)) / env.theta_threshold_radians - 0.5
new_r = r1 + r2
dqn.store_transition(s, a, new_r, s_) # 存储样本
episode_reward_sum += new_r # 逐步加上一个episode内每个step的reward
s = s_ # 更新状态
if dqn.memory_counter > MEMORY_CAPACITY: # 如果累计的transition数量超过了记忆库的固定容量2000
# 开始学习 (抽取记忆,即32个transition,并对评估网络参数进行更新,并在开始学习后每隔100次将评估网络的参数赋给目标网络)
dqn.learn()
if done: # 如果done为True
# round()方法返回episode_reward_sum的小数点四舍五入到2个数字
print('episode%s---reward_sum: %s' % (i, round(episode_reward_sum, 2)))
rewards.append(episode_reward_sum)
break
边栏推荐
- canvas基础1 - 画直线(通俗易懂)
- This time, thoroughly understand the MySQL index
- 5. Download and use of MSDN
- [modern Chinese history] Chapter 9 test
- js判断对象是否是数组的几种方式
- The latest tank battle 2022 full development notes-1
- Principles, advantages and disadvantages of two persistence mechanisms RDB and AOF of redis
- String abc = new String(“abc“),到底创建了几个对象
- The difference between cookies and sessions
- Canvas foundation 1 - draw a straight line (easy to understand)
猜你喜欢
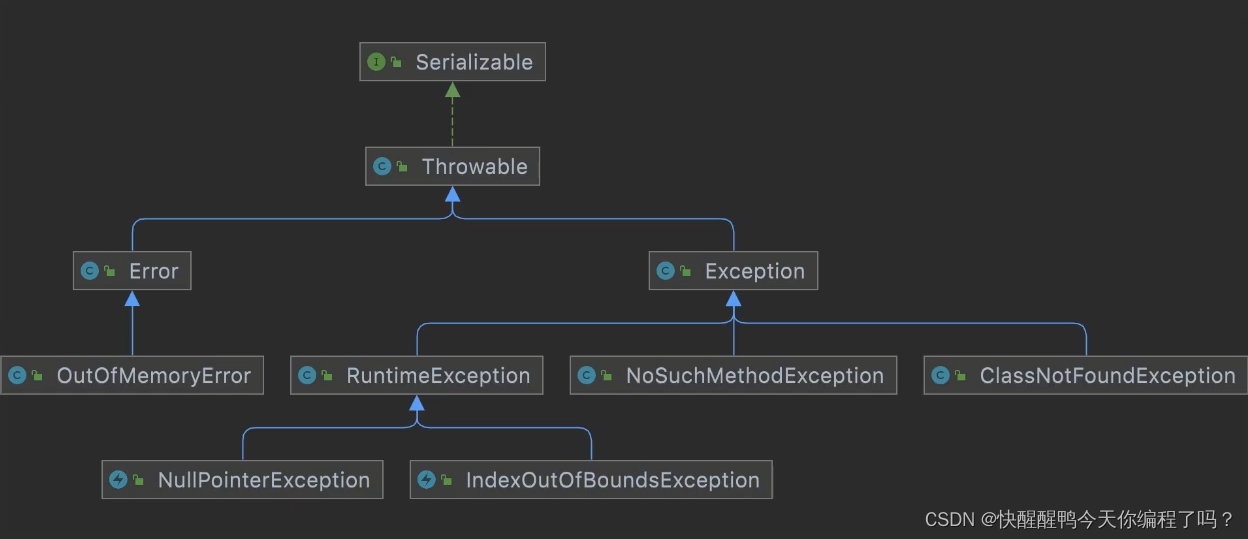
受检异常和非受检异常的区别和理解
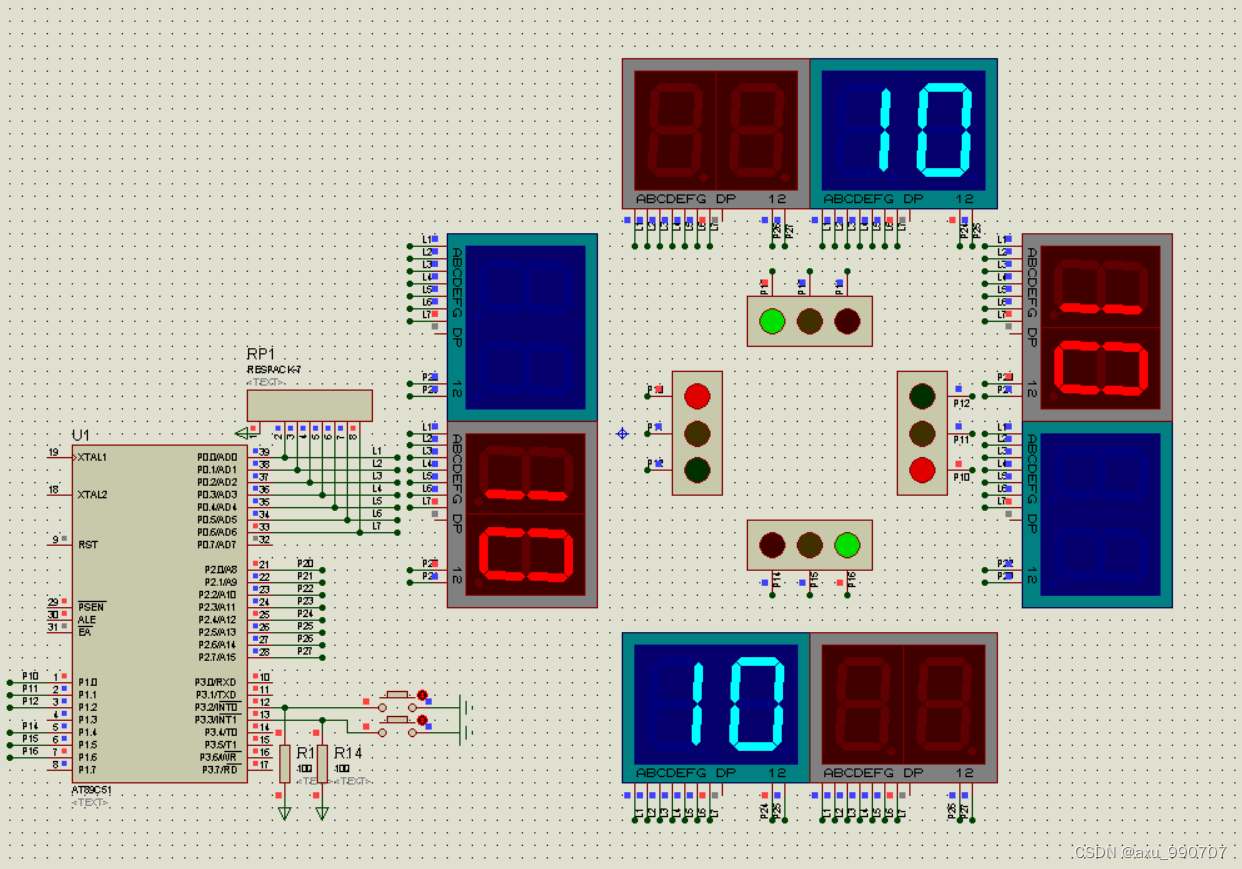
Write a program to simulate the traffic lights in real life.

【手撕代码】单例模式及生产者/消费者模式

Differences among fianl, finally, and finalize
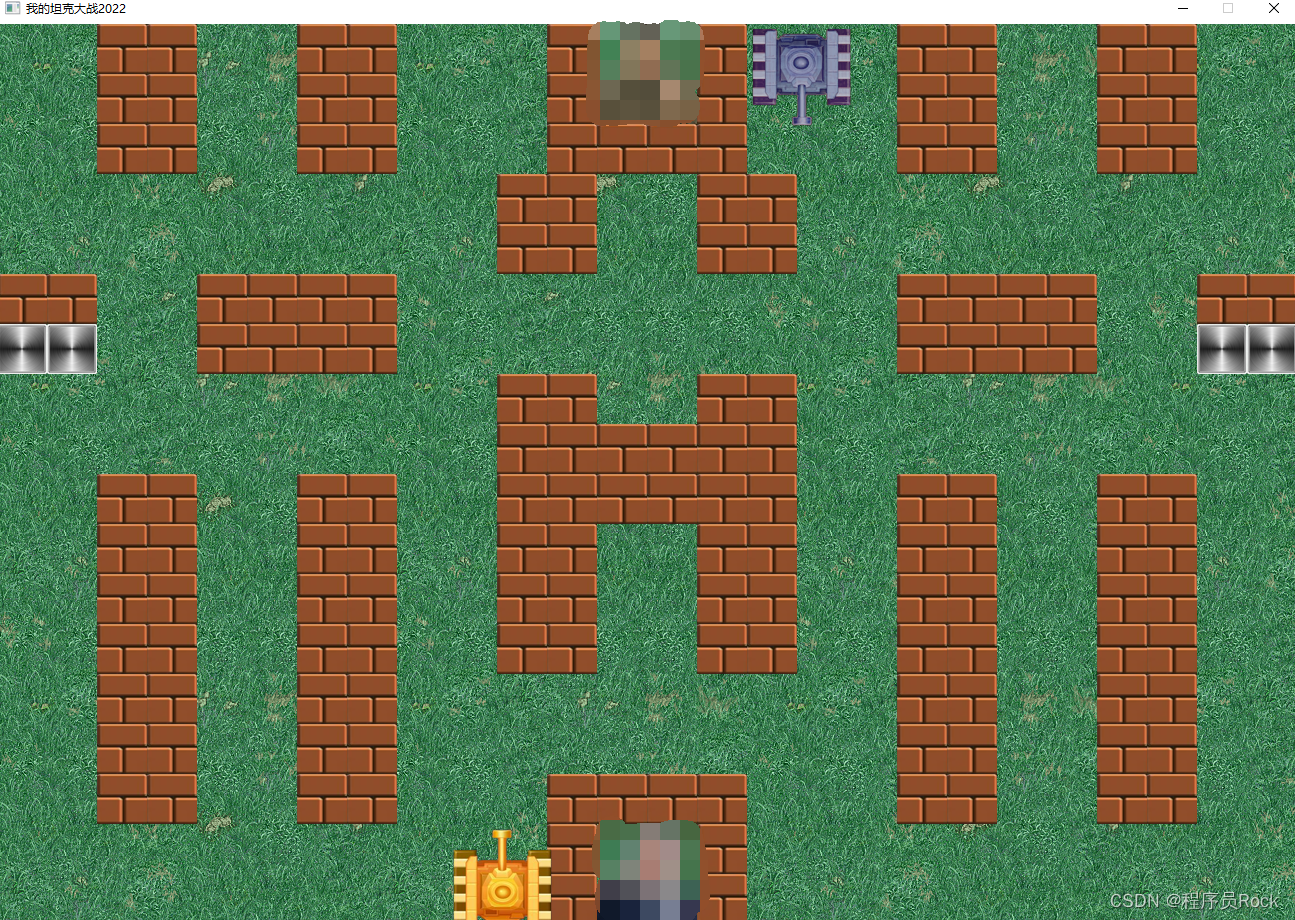
The latest tank battle 2022 - Notes on the whole development -2
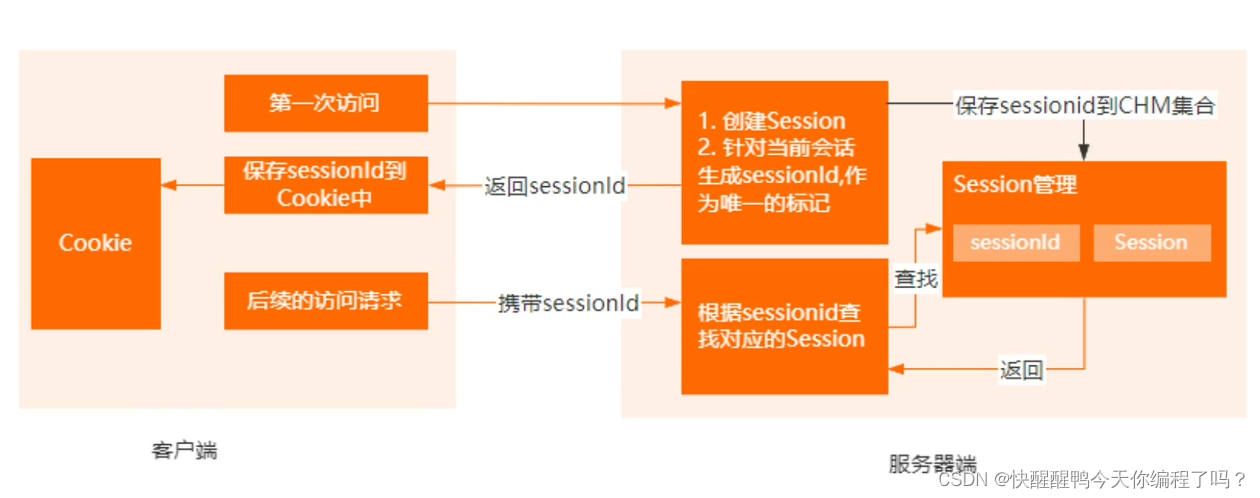
Cookie和Session的区别
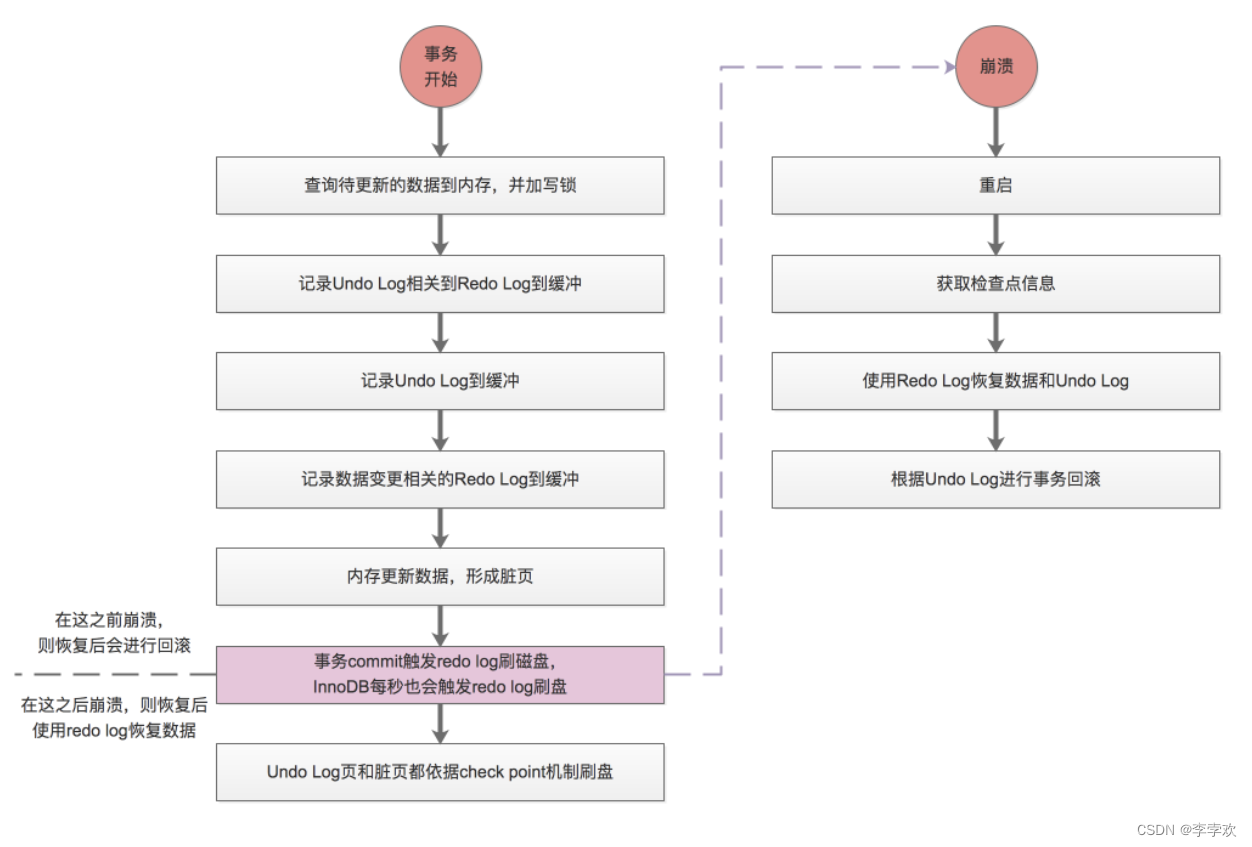
MySQL事务及实现原理全面总结,再也不用担心面试

Mortal immortal cultivation pointer-2
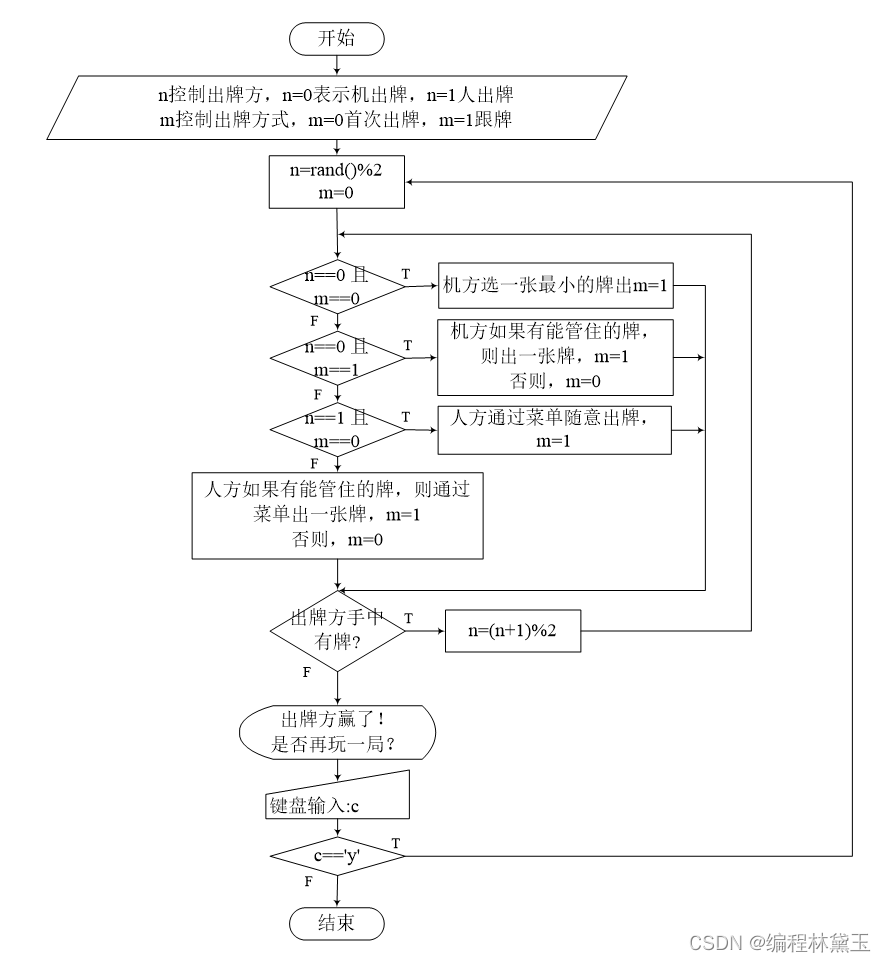
撲克牌遊戲程序——人機對抗
5. Function recursion exercise
随机推荐
Miscellaneous talk on May 14
扑克牌游戏程序——人机对抗
Write a program to simulate the traffic lights in real life.
抽象类和接口的区别
【VMware异常问题】问题分析&解决办法
实验七 常用类的使用(修正帖)
The latest tank battle 2022 - full development notes-3
A comprehensive summary of MySQL transactions and implementation principles, and no longer have to worry about interviews
2022 Teddy cup data mining challenge question C idea and post game summary
【毕业季·进击的技术er】再见了,我的学生时代
Using spacedesk to realize any device in the LAN as a computer expansion screen
js判断对象是否是数组的几种方式
实验八 异常处理
ABA问题遇到过吗,详细说以下,如何避免ABA问题
Cookie和Session的区别
Mortal immortal cultivation pointer-1
Miscellaneous talk on May 27
The difference between cookies and sessions
为什么要使用Redis
【手撕代码】单例模式及生产者/消费者模式