2021 Li Hongyi machine learning (3): what if neural network training fails

1 Mission Introduction

1.1 If on the training set loss Always not small enough

• Situation 1 ：model bias（ The model itself has great limitations ）—— Build more complex models
• Situation two ： optimization problem （ The optimization method used cannot be optimized to loss minimum value ）—— More effective optimization methods

How to judge what kind of situation ？

• First, train on a shallow network that is easier to optimize
• If the deep network cannot get smaller than the above on the training set loss, It is case two

1.2 If loss On the training set , On the test set

• Situation 1 ：overfitting—— The simplest solution is to add training data Data augmentation：
  
  The original data can be processed , Get new data that can be added to the training set ： The first picture above is the original , second 、 The three pictures are the inversion and local enlargement of the original picture . And the fourth picture is the picture upside down , This makes model recognition more difficult , So the method of the fourth picture is not good .
  The second method is to add restrictions to the model , For example, the model must be a conic , But be careful not to limit too much .
  How to select a model ？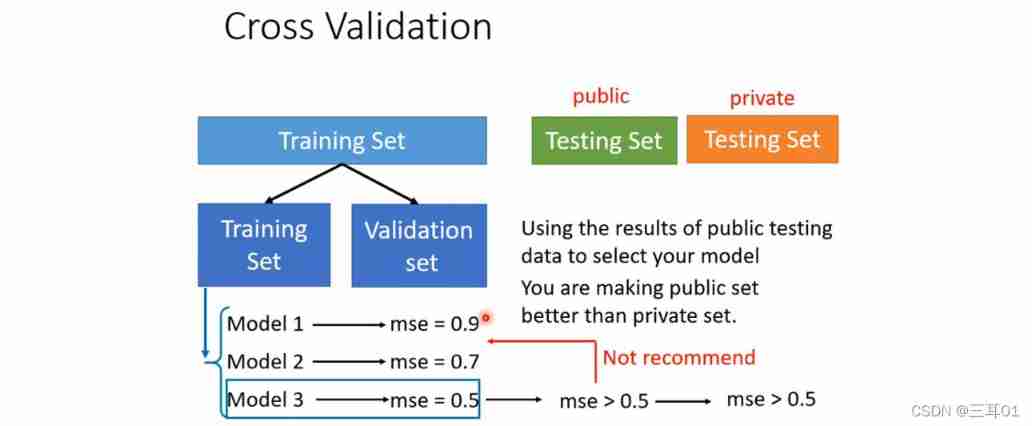
  
• Situation two ：mismatch
  overfitting It can be solved by adding the data of the training set , however mismatch Of training and testing Different distribution of , It can't be solved like that
  

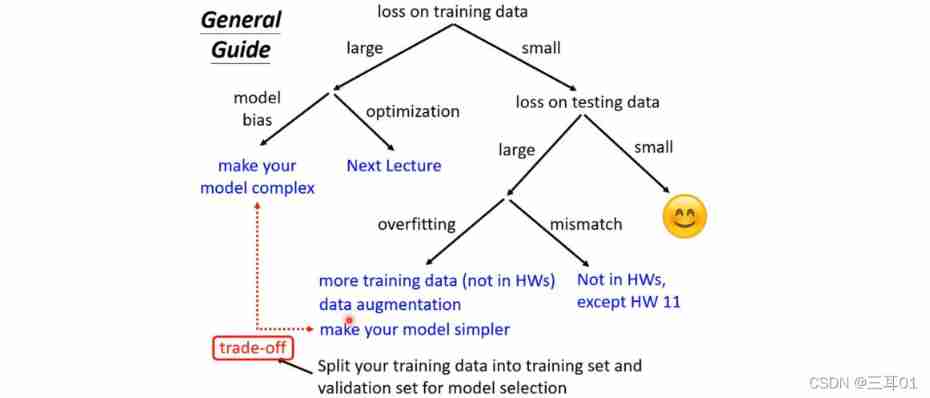
1.3 Schematic diagram of mission strategy

2 Local minimum (local minima) And saddle point (saddle point)

When loss When unable to descend , Maybe the gradient is close 0 了 , This is a , Local minimum (local minima) And saddle point (saddle point) It's possible , They are collectively referred to as critical point.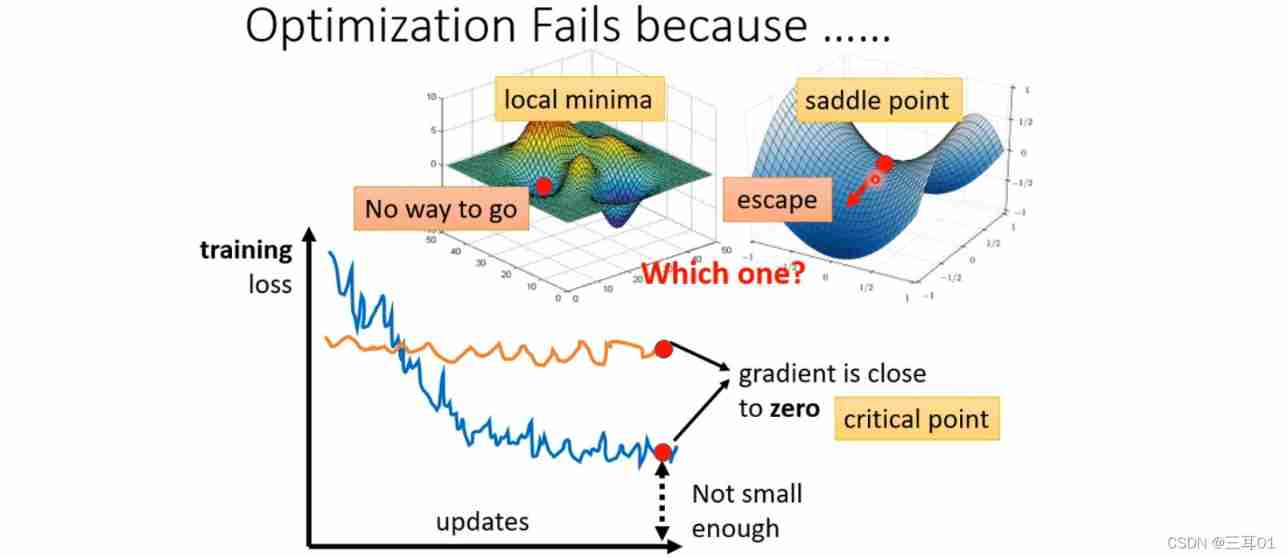
here , We need to judge which situation it belongs to , Calculation Hessian that will do ：

give an example ：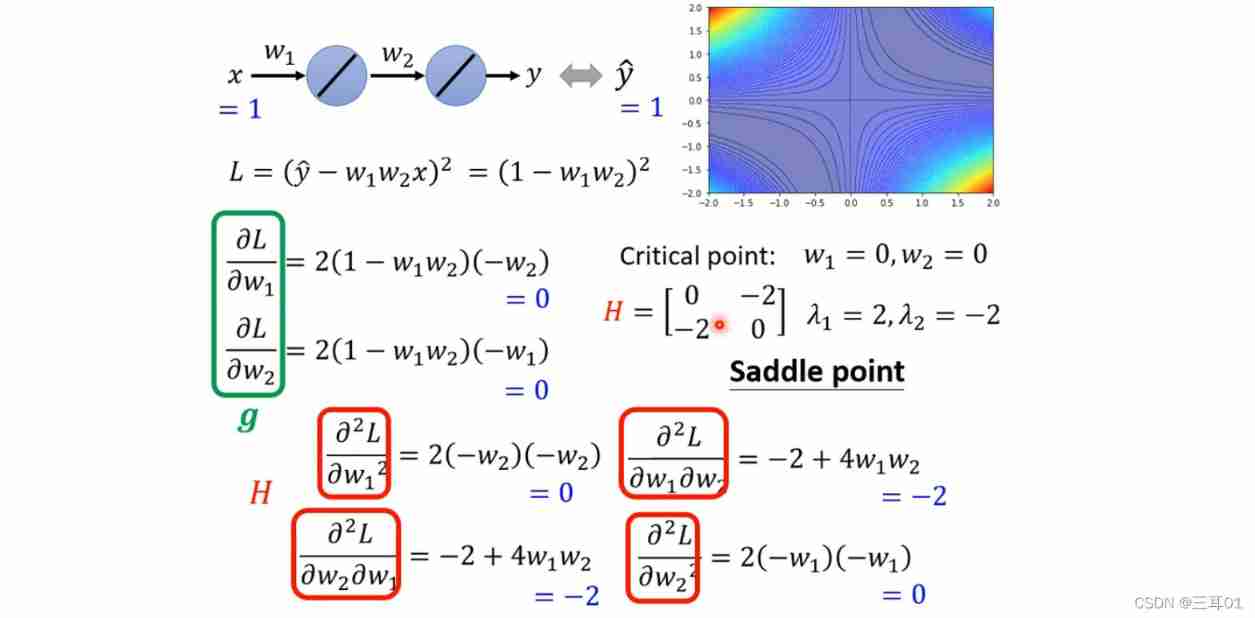

If it's a saddle point (saddle point), You can also find the direction of descent and continue training .

But in fact, this kind of situation is rare .

3 batch （batch） And momentum （momentum）

3.1 batch （batch）

Small batch size Have better results .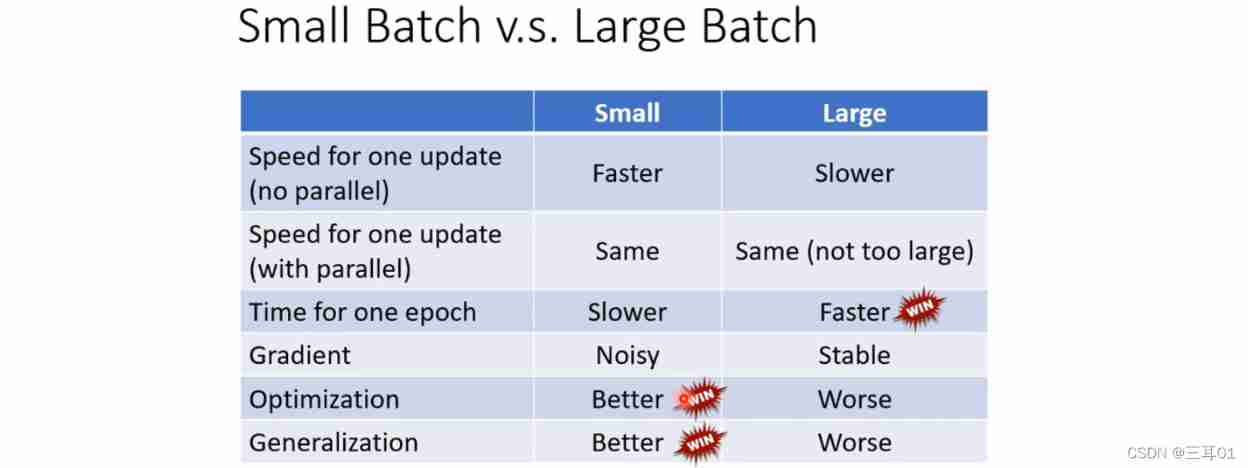

There are many articles that want to have it both ways ：

3.2 momentum （momentum）

With momentum , Will not stay in critical point, But will continue down ：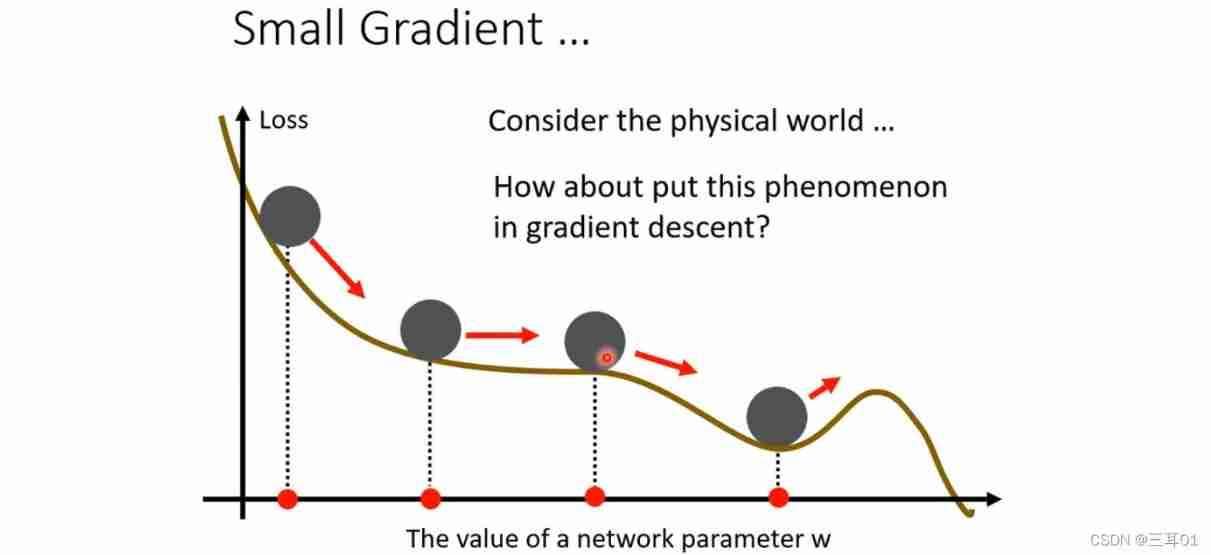

The previous gradient descent is like this ：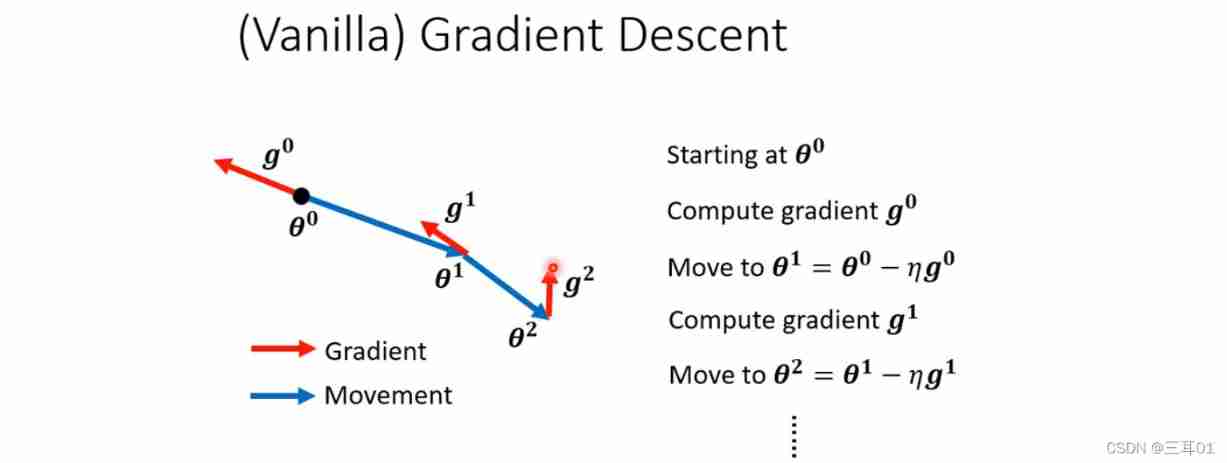

After adding momentum , Is to add the consideration of the previous action , Then the next action is the result of the combination of the previous action and the previous action .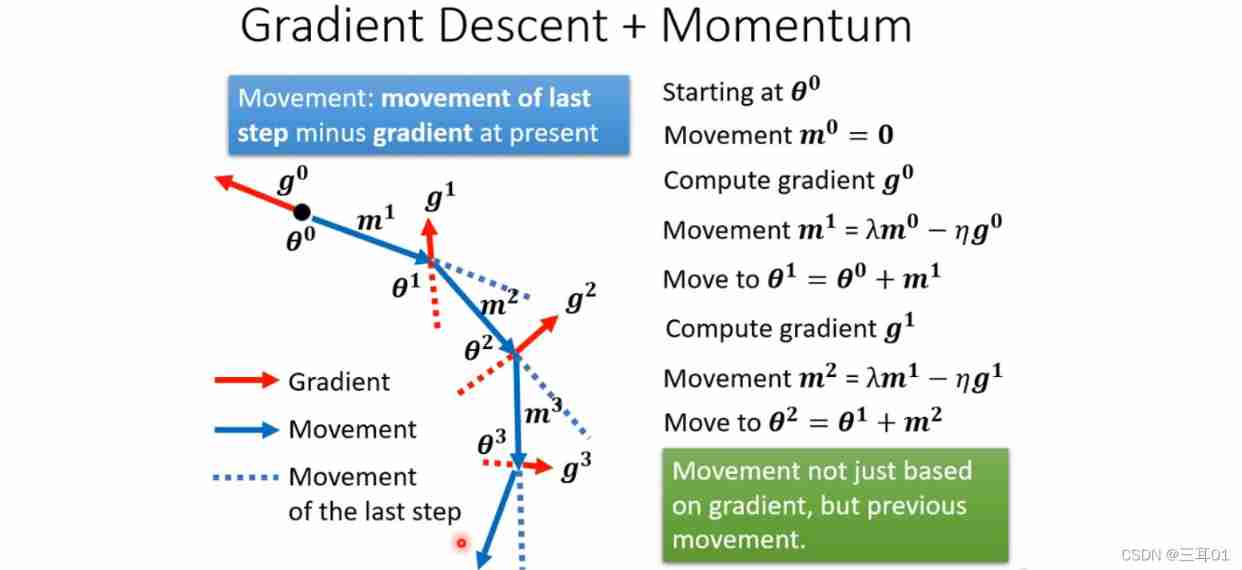

The red line below is the gradient , The blue dotted line is momentum , The blue solid line is the result of the combination of the first two , You can see , Maybe even climb over the hill , Reach the real loss minimum value .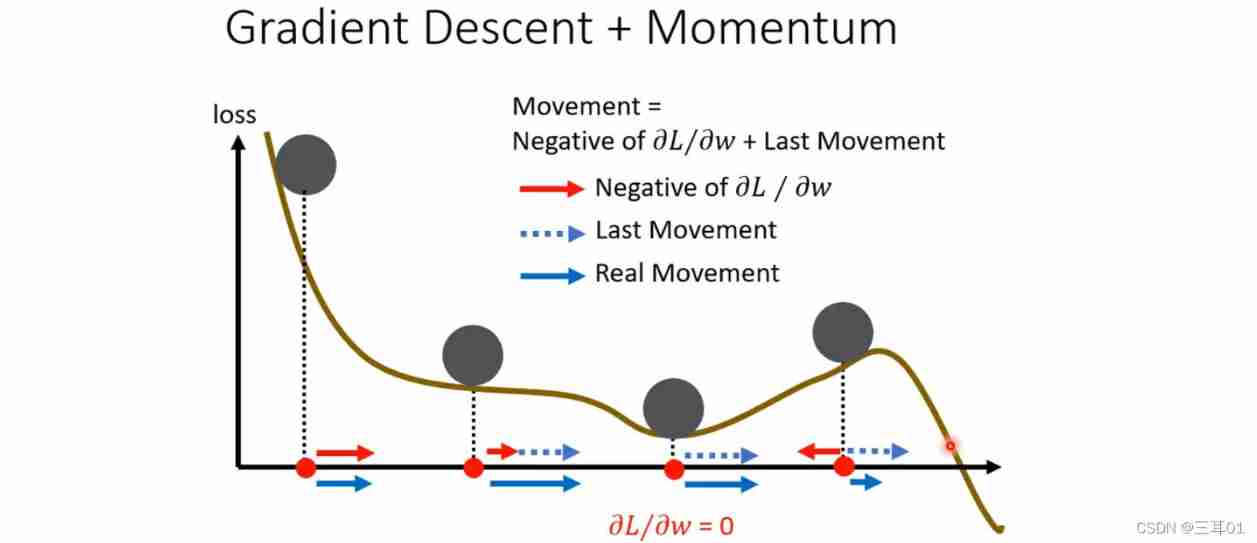

4 Automatically adjust the learning rate (Learning Rate)

In the front loss When not falling , We said it might be critical point, But it may also be the following ：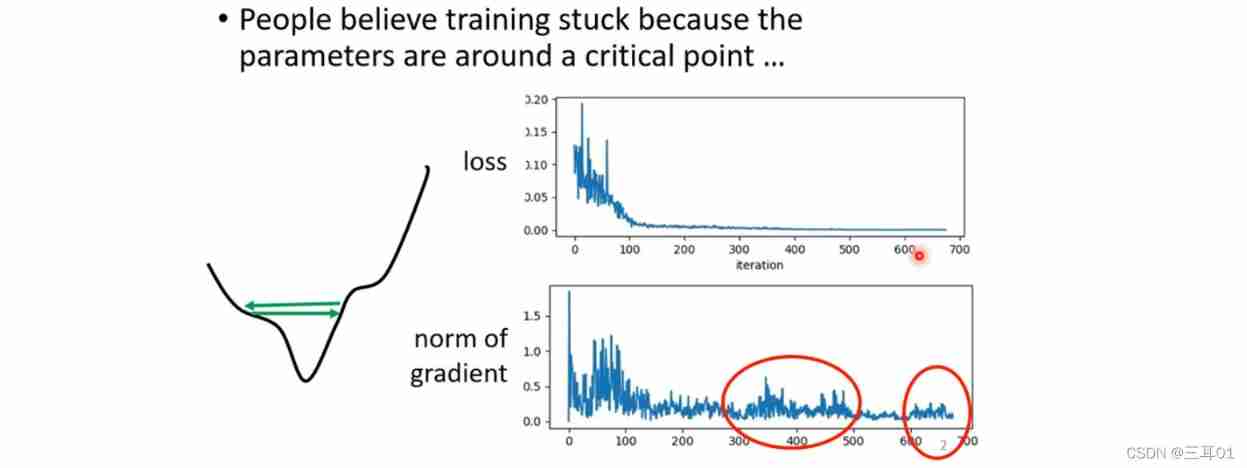

learning rate It should be customized for each parameter ：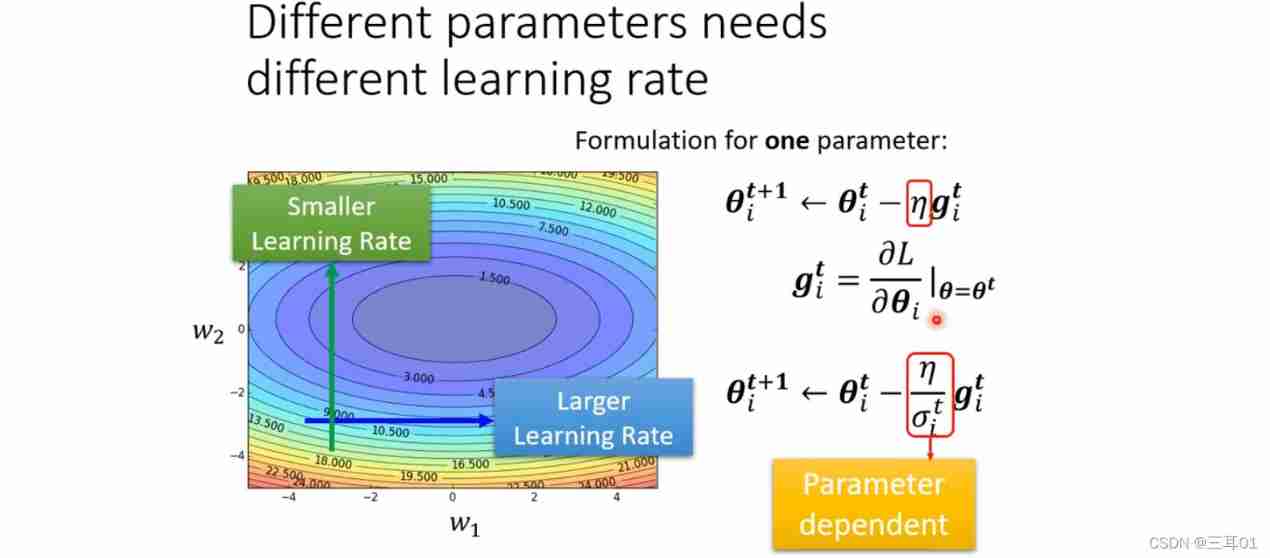

Number of original parameters $t+1$ In the next iteration , Learning rate $\eta$ It is the same. ; And after we modify ,$\eta$ Turned into $\frac{\eta }{{\sigma }_i^t}$, After this modification , The learning rate is parameter independent Of course. , It's also iteration independent Of （ Parameter independent 、 Iterative independence ）.

4.1 The most common way to modify the learning rate is the root mean square

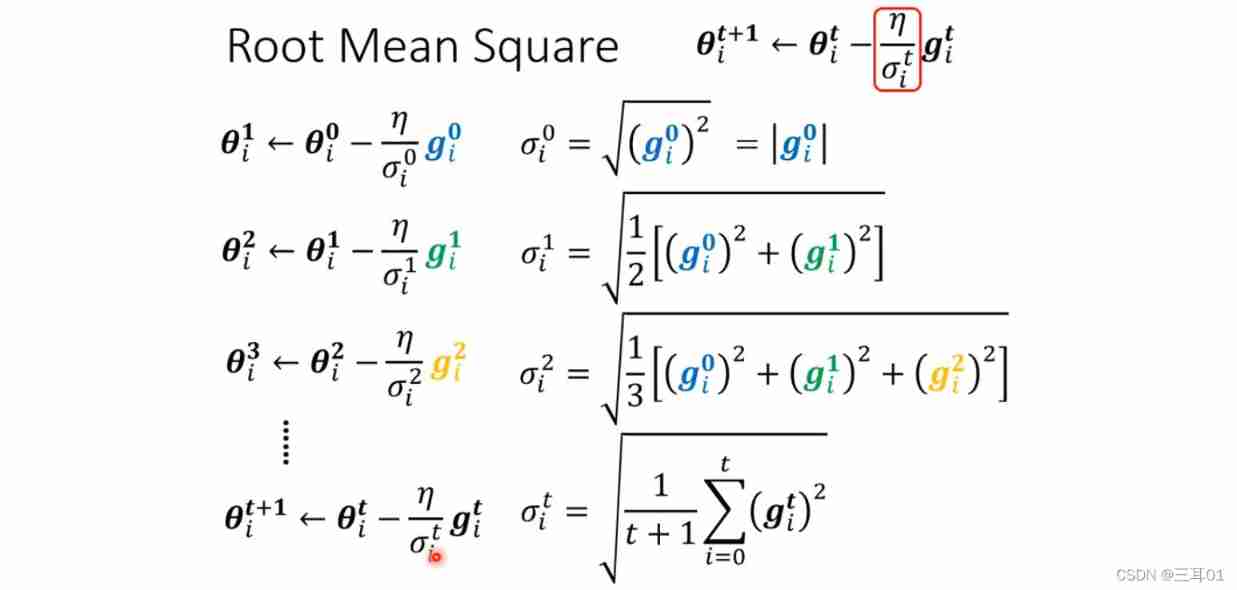
This method is used in Adagrad Inside ：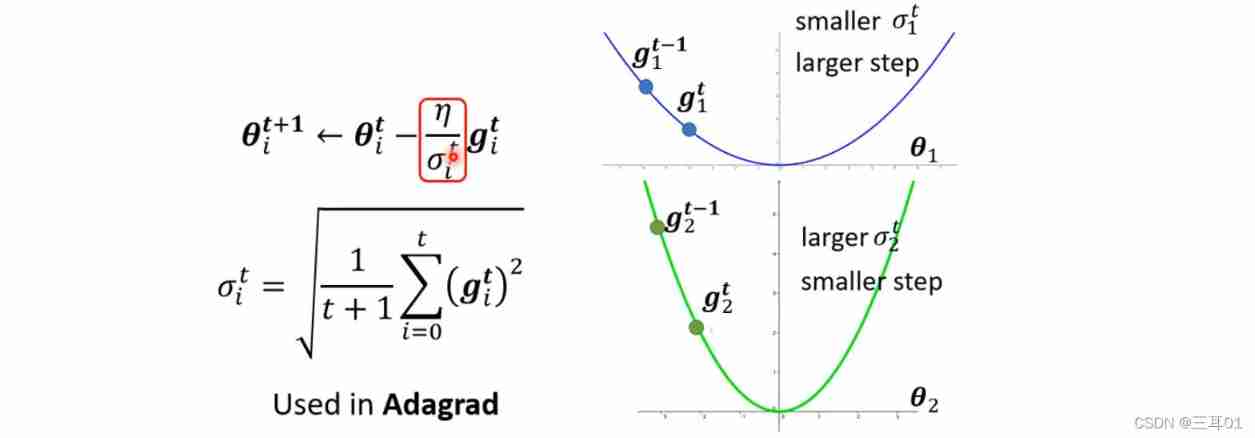

When the gradient is small , Calculated ${\sigma }_i^t$ Just small , Then the learning rate is large ; On the contrary, the learning rate becomes smaller .

4.2 You can adjust your current gradient Importance ——RMSProp

This method is achieved by setting $\alpha$ To adjust the importance of the current gradient ：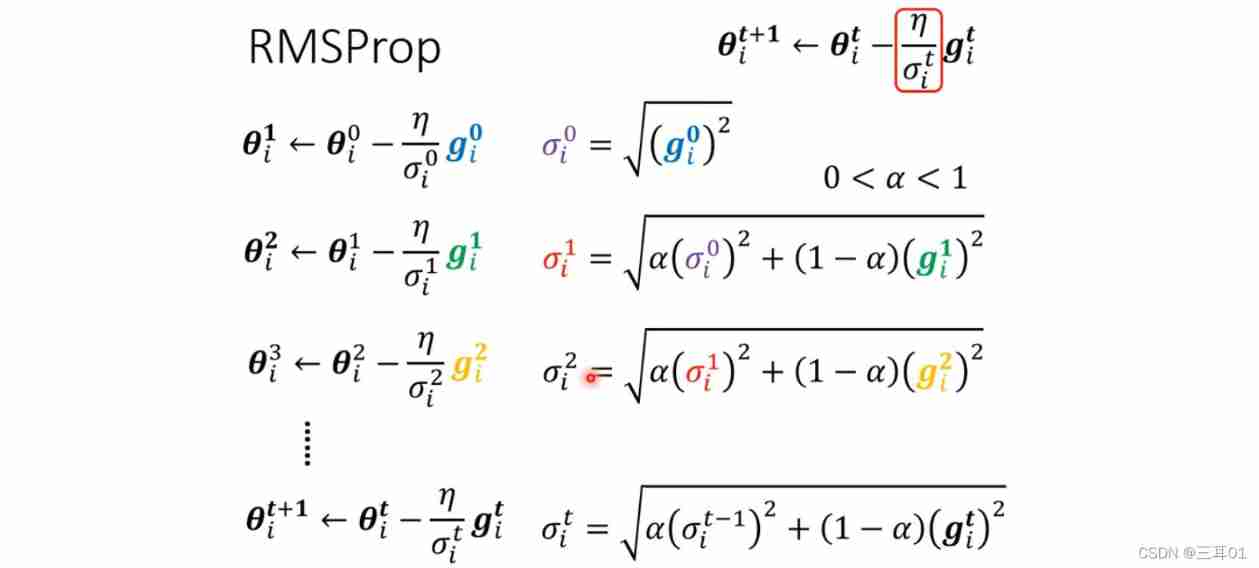

As shown in the figure below ：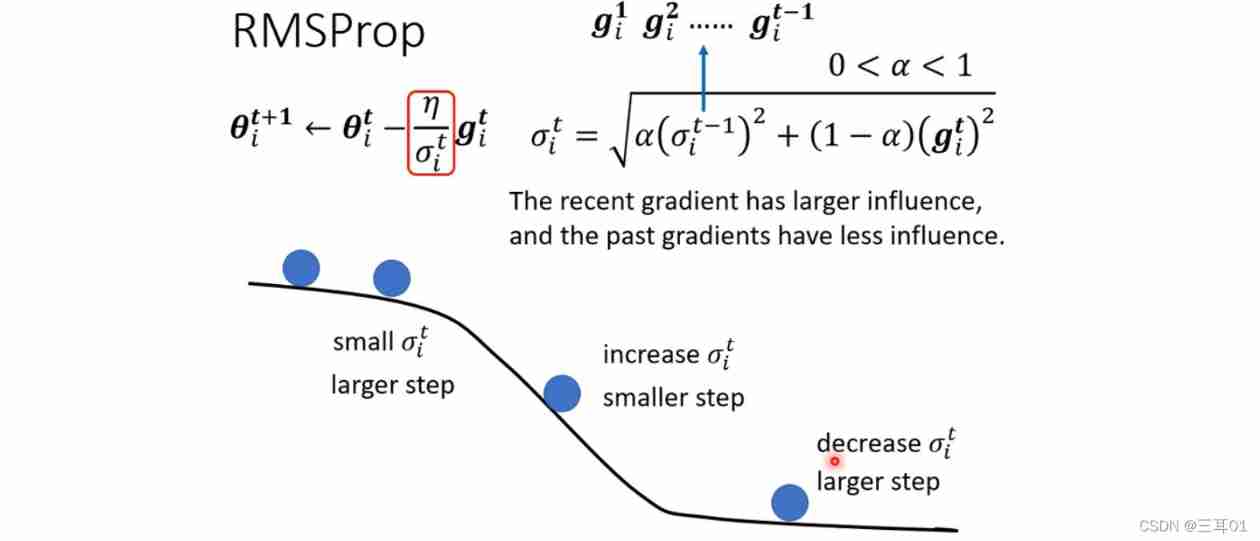

You can adjust $\alpha$ The relatively small , Give Way ${\sigma }_i^t$ More dependent $g_i^t$, such , When the gradient suddenly changes from smooth to steep ,$g_i^t$ Bigger ,${\sigma }_i^t$ It's getting bigger , It will make the pace at this time smaller ; Empathy , When the gradient turns smooth again ,${\sigma }_i^t$ Will quickly become smaller , The pace will get bigger .
In fact, it is to make every step react quickly according to the changing situation .

4.3 Adam: RMSProp + Momentum

4.4 Learning Rate Scheduling

Make learning rate $\eta$ Over time ：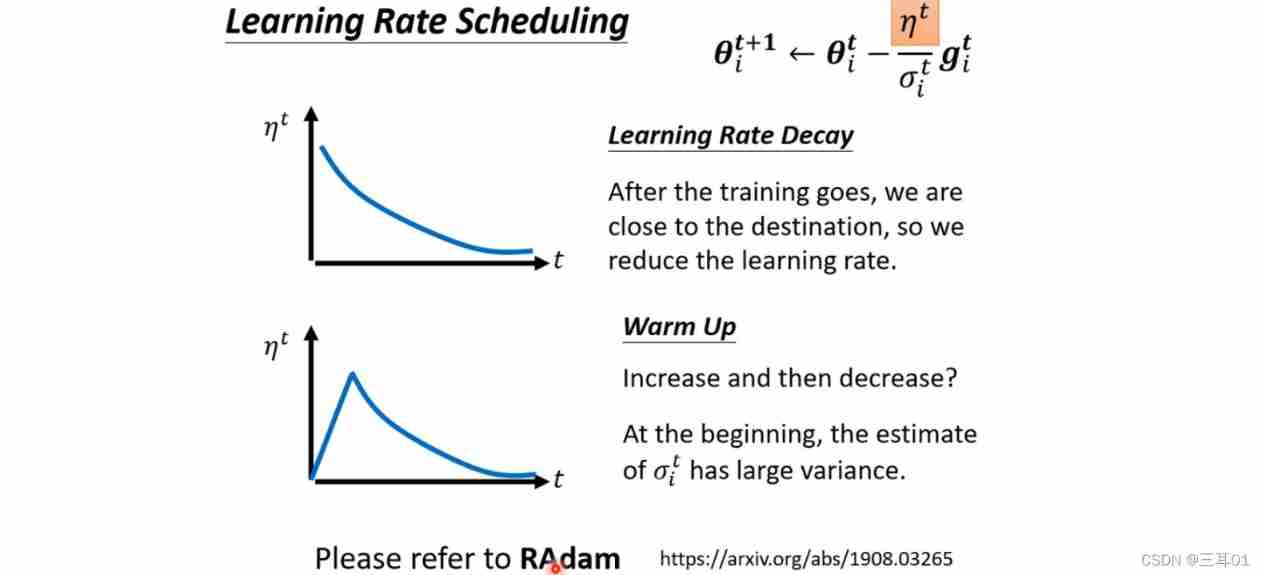

4.5 summary

Add the front 3.2, We use three methods to improve gradient descent ： momentum 、 Adjust the learning rate 、 The learning rate changes over time .
$m_i^t$ and ${\sigma }_i^t$ Will not offset each other , because $m_i^t$ Including the direction , and ${\sigma }_i^t$ Only in size .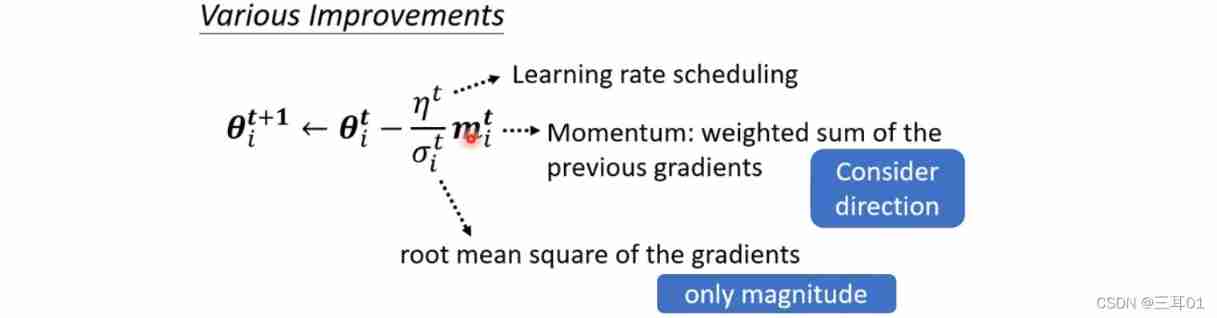

5 Loss function (Loss) It may also have an impact

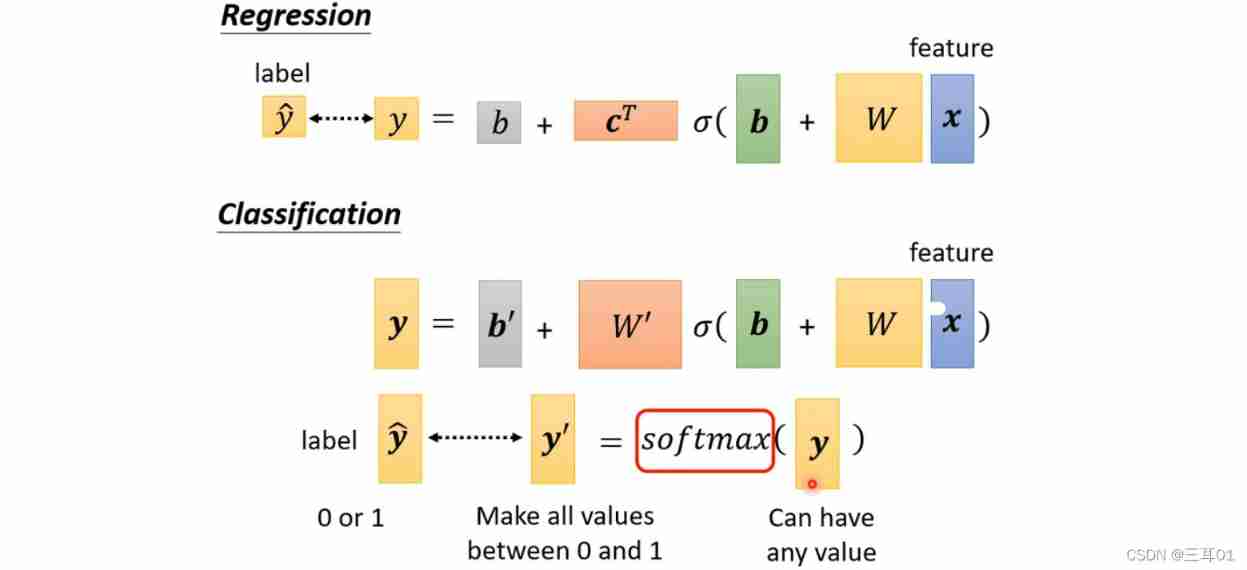
In classification , It's usually added softmax：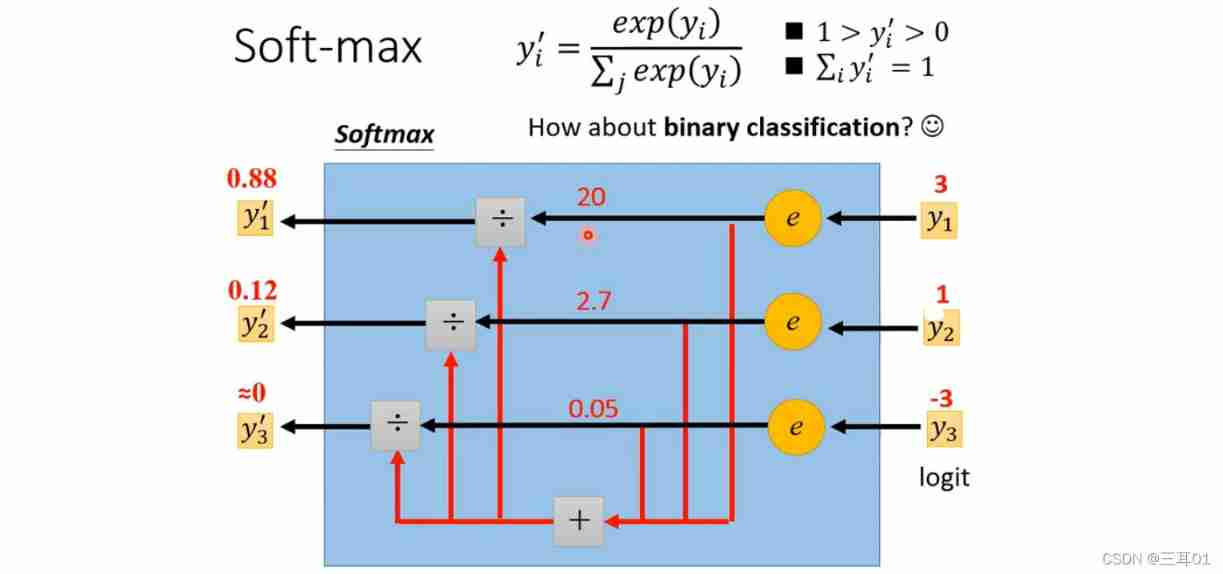

If it is classified into two categories , Is more commonly used sigmoid, But in fact, the results of these two methods are the same .

Here is the loss function ：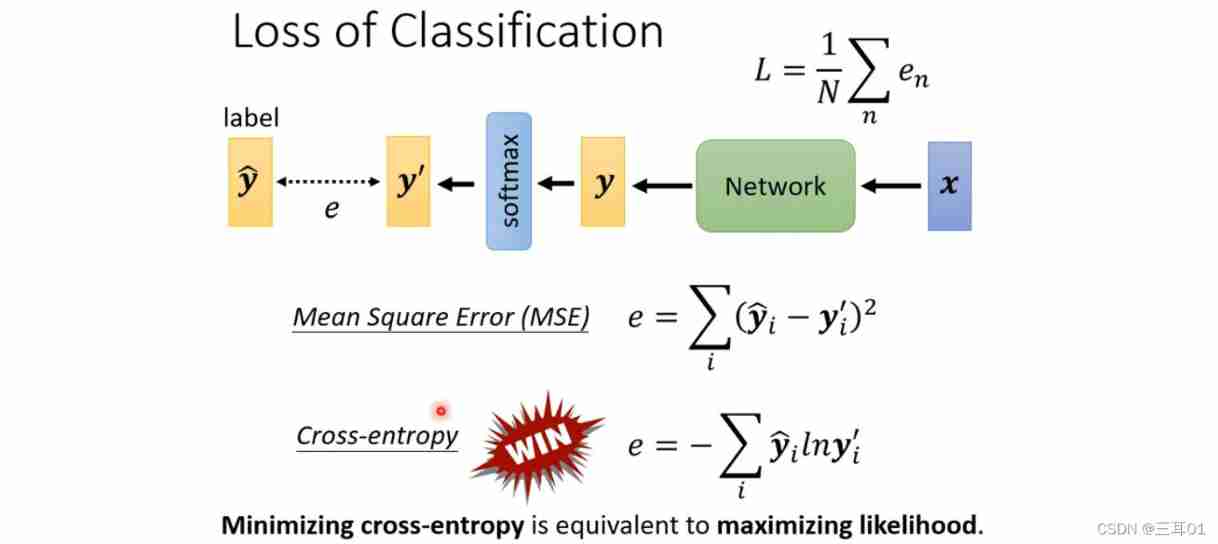

in fact , Cross entropy in classification is The most commonly used Of , stay PyTorch in ,CrossEntropyLoss This function already contains softmax, The two are bound together .

Why? ？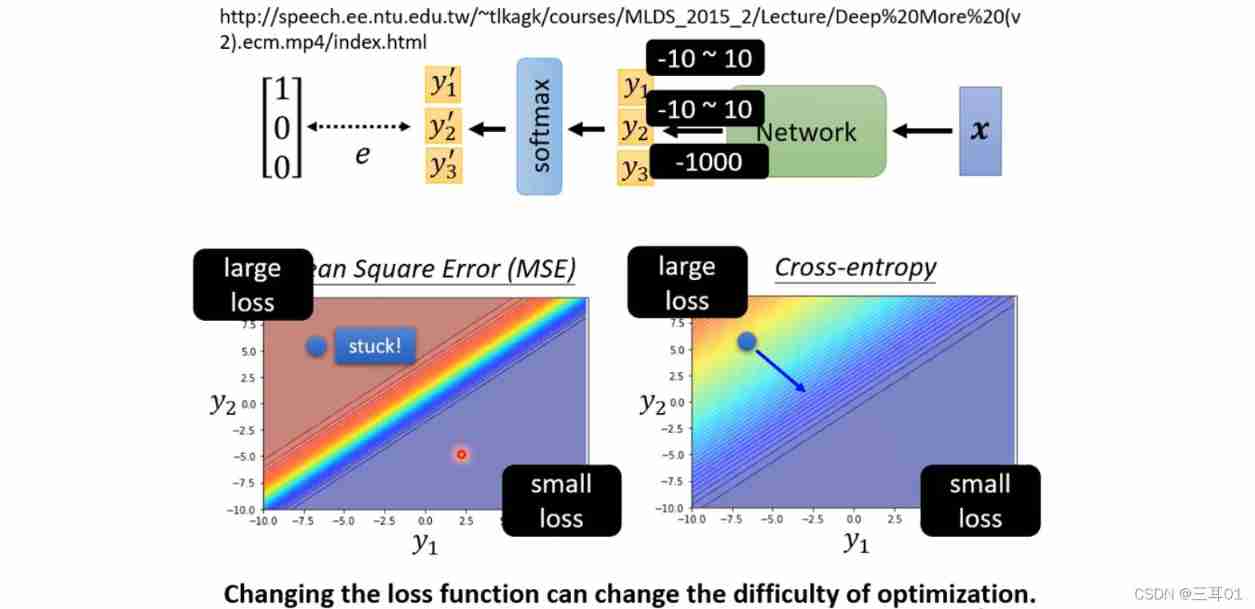

As you can see from the diagram , When loss When a large ,MSE Very flat , Cannot gradient down to loss A small place , Get stuck ; But the cross entropy can decline all the way .

6 Batch standardization （Batch Normalization）

Hope for different parameters , Yes loss The scope of influence is relatively uniform , Like the right figure below ：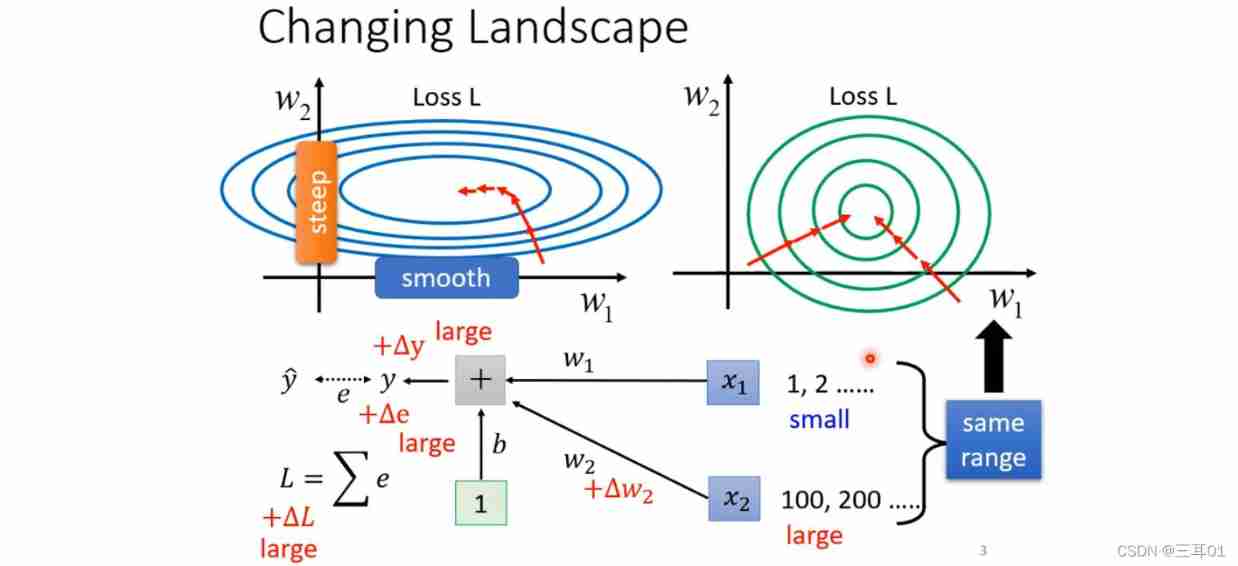

The method is feature normalization （Feature Normalization）：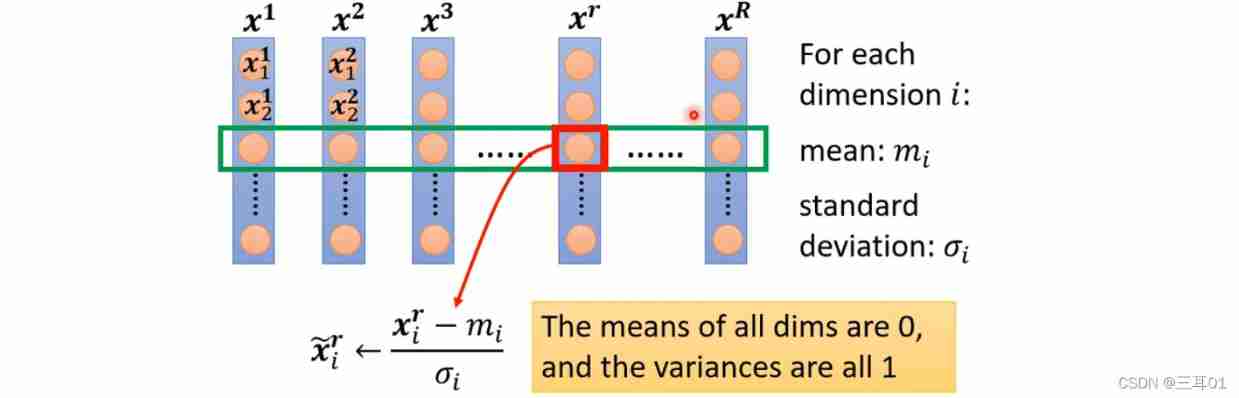

After normalization , The average value of the characteristics of each dimension is 0, The variance of 1.
Generally speaking , Feature normalization makes gradient descent converge faster .

The output of the next step also needs to be normalized , These normalization are aimed at a Batch Of ：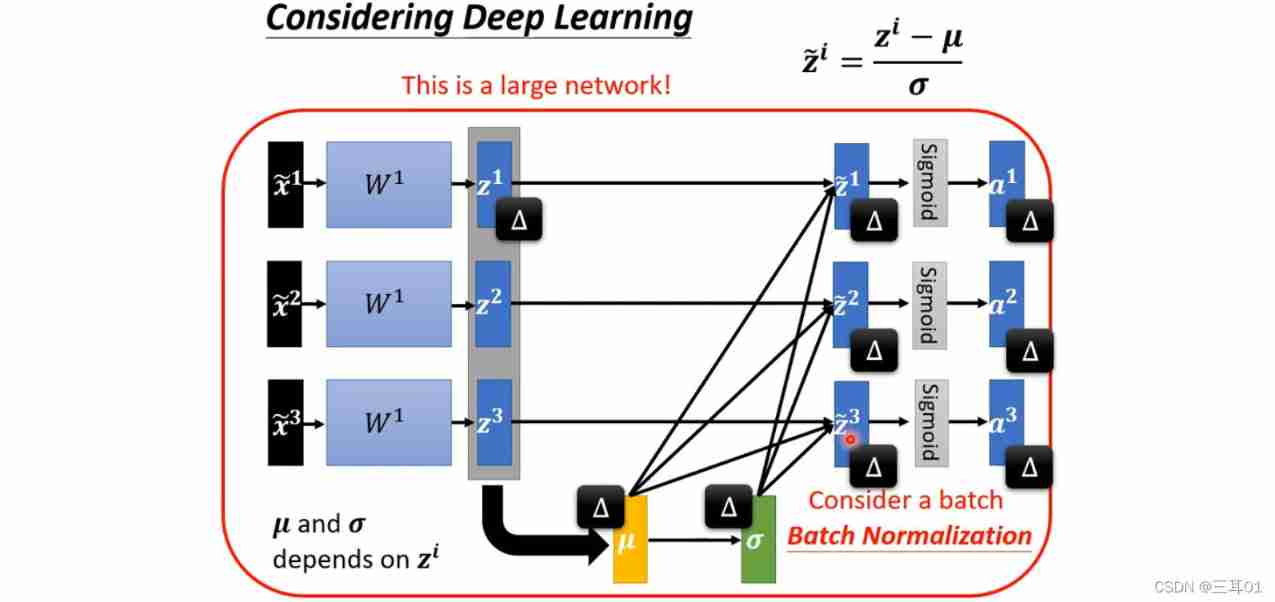

In order to make the mean value of the output not 0, The variance is not 1, It will add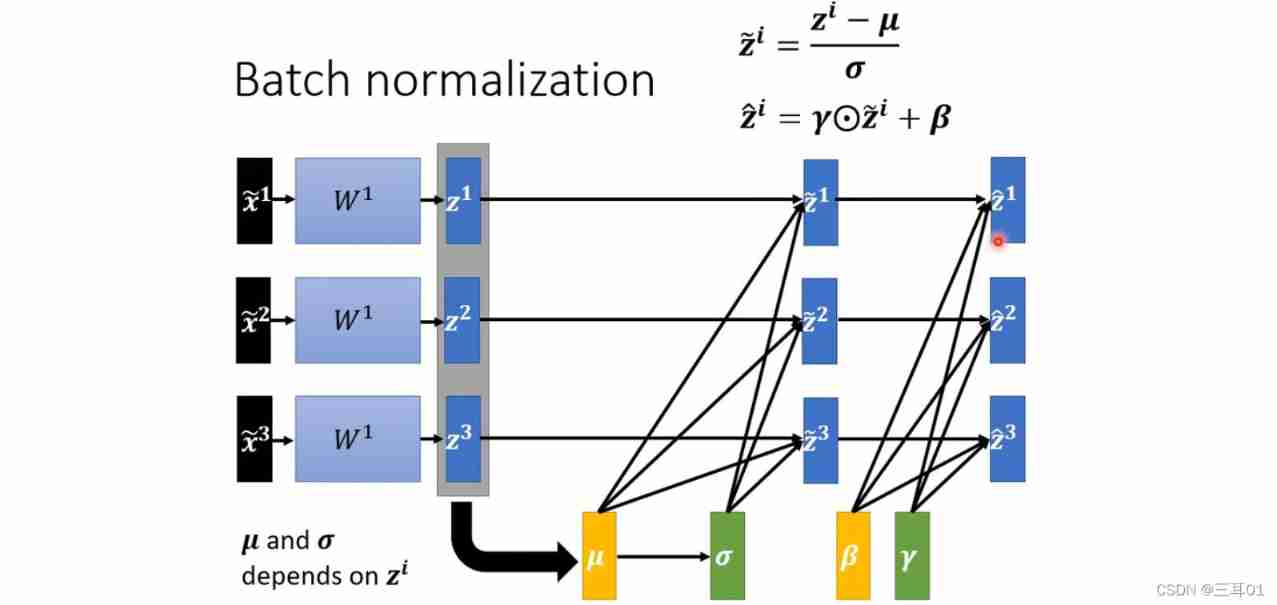 $\beta$ and $\gamma$：

$\beta$ and $\gamma$ The initial values of these two vectors are 0 and 1, Then learn and update in the network step by step , So at the beginning ,dimension The distribution of is close , follow-up error surface After performing better , That's what makes $\beta$ and $\gamma$ add .

stay Testing in ： take train Parameters of are used in test in .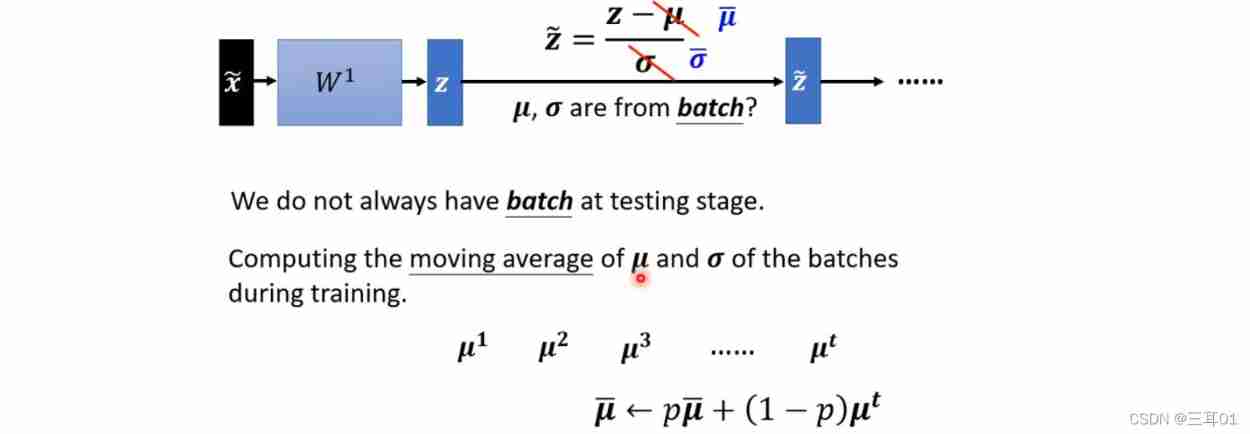

Some famous Normalization：