当前位置:网站首页>LeetCode 1640. Can I connect to form an array
LeetCode 1640. Can I connect to form an array
2022-07-06 16:43:00 【Daylight629】
1640. Can you join to form an array
Give you an array of integers arr , Every integer in the array Different from each other . There's another array of integers pieces, The integers are also Different from each other . Please use In any order Connect pieces In order to form arr . however , Don't allow For each array pieces[i] Reorder integers in .
If you can connect pieces The array in the form of arr , return true ; otherwise , return false .
Example 1:
Input :arr = [85], pieces = [[85]]
Output :true
Example 2:
Input :arr = [15,88], pieces = [[88],[15]]
Output :true
explain : Connect in turn [15] and [88]
Example 3:
Input :arr = [49,18,16], pieces = [[16,18,49]]
Output :false
explain : Even if the numbers match , You can't rearrange pieces[0]
Example 4:
Input :arr = [91,4,64,78], pieces = [[78],[4,64],[91]]
Output :true
explain : Connect in turn [91]、[4,64] and [78]
Example 5:
Input :arr = [1,3,5,7], pieces = [[2,4,6,8]]
Output :false
Tips :
1 <= pieces.length <= arr.length <= 100sum(pieces[i].length) == arr.length1 <= pieces[i].length <= arr.length1 <= arr[i], pieces[i][j] <= 100arrThe integer Different from each otherpiecesThe integer Different from each other ( in other words , If you willpiecesFlatten it into a one-dimensional array , All integers in an array are different from each other )
Two 、 Method 1
Hash
class Solution {
public boolean canFormArray(int[] arr, int[][] pieces) {
Map<Integer, int[]> map = new HashMap<>();
for (int[] piece : pieces) {
map.put(piece[0], piece);
}
for (int i = 0; i < arr.length;) {
int cur = arr[i];
if (map.containsKey(cur)) {
int[] pos = map.get(cur);
for (int x : pos) {
if (arr[i] == x) {
i++;
} else {
return false;
}
}
} else {
return false;
}
}
return true;
}
}
Complexity analysis
Time complexity :O(n).
Spatial complexity :O(n).
边栏推荐
- LeetCode 1447. Simplest fraction
- 875. Leetcode, a banana lover
- It is forbidden to trigger onchange in antd upload beforeupload
- Kubernetes集群部署
- Spark独立集群Worker和Executor的概念
- 简单尝试DeepFaceLab(DeepFake)的新AMP模型
- (POJ - 1458) common subsequence (longest common subsequence)
- Li Kou leetcode 280 weekly match
- How to insert mathematical formulas in CSDN blog
- Tree of life (tree DP)
猜你喜欢

业务系统兼容数据库Oracle/PostgreSQL(openGauss)/MySQL的琐事

字节跳动新程序员成长秘诀:那些闪闪发光的宝藏mentor们
两个礼拜速成软考中级软件设计师经验
Chapter 7__ consumer_ offsets topic
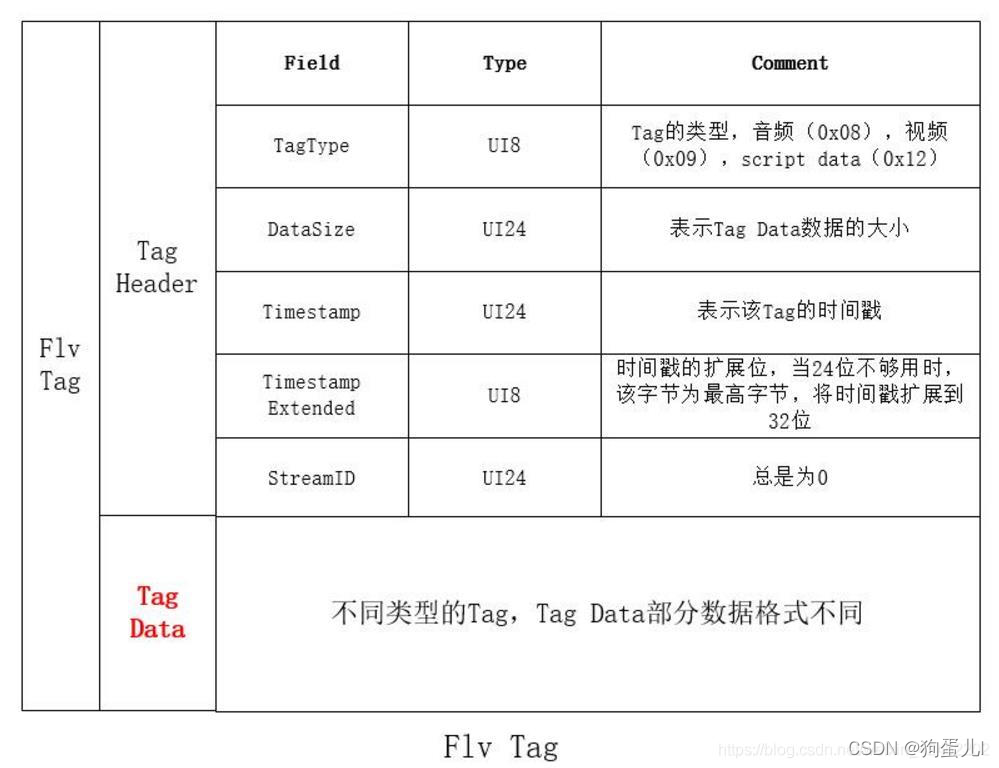
Detailed explanation of FLV format
CMake速成
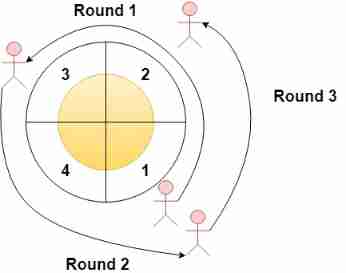
LeetCode 1560. The sector with the most passes on the circular track

QT implementation window gradually disappears qpropertyanimation+ progress bar
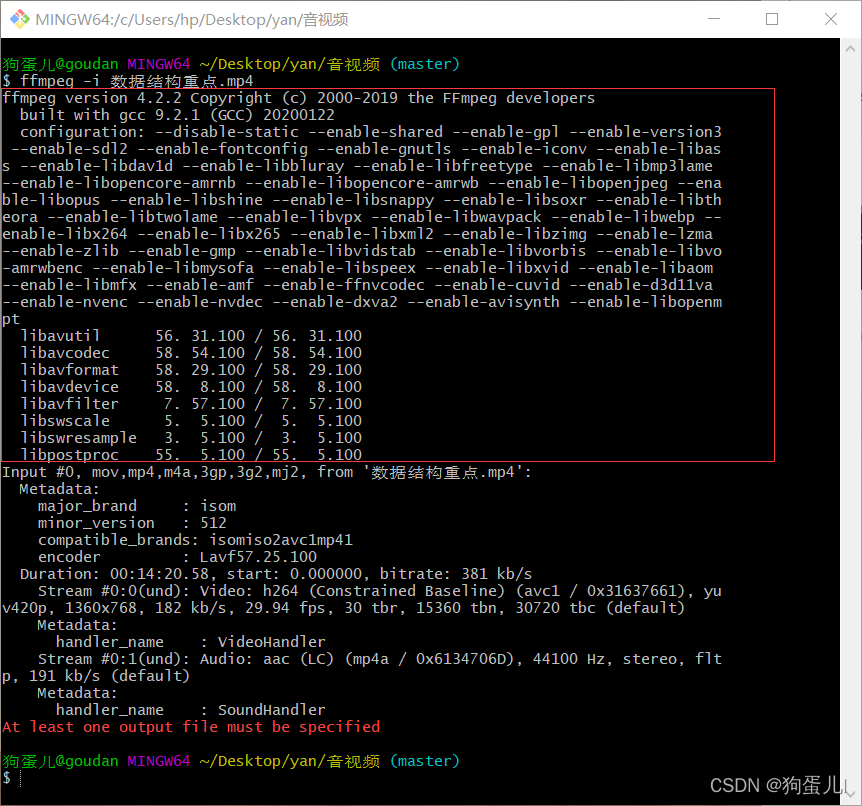
Ffmpeg command line use
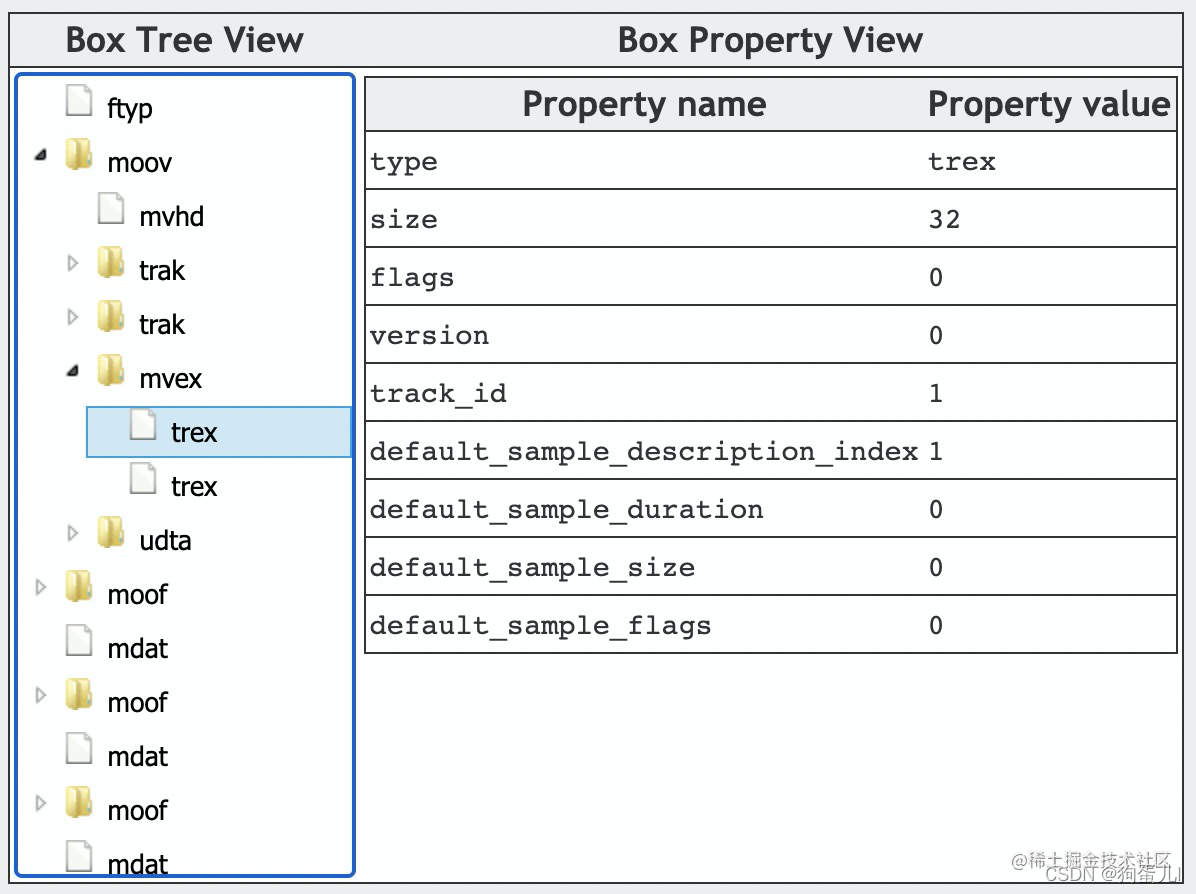
Mp4 format details
随机推荐
Install Jupiter notebook under Anaconda
China double brightening film (dbef) market trend report, technical dynamic innovation and market forecast
第5章 NameNode和SecondaryNameNode
875. Leetcode, a banana lover
(lightoj - 1349) Aladdin and the optimal invitation (greed)
音视频开发面试题
LeetCode 1550. There are three consecutive arrays of odd numbers
去掉input聚焦时的边框
Codeforces Round #799 (Div. 4)A~H
Li Kou: the 81st biweekly match
Market trend report, technological innovation and market forecast of desktop electric tools in China
The concept of spark independent cluster worker and executor
Codeforces Round #771 (Div. 2)
第5章 消费者组详解
QT realizes window topping, topping state switching, and multi window topping priority relationship
Tencent interview algorithm question
Solve the problem that intel12 generation core CPU single thread only runs on small cores
第2章 HFDS的Shell操作
Research Report on market supply and demand and strategy of China's tetraacetylethylenediamine (TAED) industry
Market trend report, technical innovation and market forecast of China's desktop capacitance meter