当前位置:网站首页>[the Nine Yang Manual] 2020 Fudan University Applied Statistics real problem + analysis
[the Nine Yang Manual] 2020 Fudan University Applied Statistics real problem + analysis
2022-07-06 13:31:00 【Elder martial brother statistics】
Catalog
The real part
One 、(20 branch ) A family has two children , Find the probability of the following events :
(1)(10 branch ) The first one is known to be a girl , Find the probability that the second is a girl ;
(2)(10 branch ) One is known to be a girl , Find the probability that the other is a girl .
Two 、(15 branch ) Jiayou 21 A coin , B has 20 A coin , Both of them toss all the coins at the same time , Find the probability that the number of coins with a facing up is more than that of B .
3、 ... and 、(15 branch ) There are countless parallel lines on the plane , Every two parallel lines are spaced 2 rice , Use side length 1 An equilateral triangle of meters is thrown at the plane , Find the probability of triangle pressing to a straight line .
Four 、(15 branch ) 8 A boy 、7 Two girls sit in a row , set up X i = 1 X_{i}=1 Xi=1 It means the first one i i i The first position is the same as i + 1 i+1 i+1 The opposite sex sits in this position , X i = 0 X_{i}=0 Xi=0 It means the first one i i i The first position is the same as i + 1 i+1 i+1 Sitting in the same seat , ξ = ∑ i = 1 14 X i , \xi=\sum_{i=1}^{14} X_{i}, ξ=∑i=114Xi, seek E ξ . E \xi . Eξ.
5、 ... and 、(15 branch ) Cite an expectation that tends to be positive and infinite , But it converges to 0 A sequence of random variables { X n } \left\{X_{n}\right\} { Xn}.
6、 ... and 、(20 branch ) Some come from the general X ∼ f ( x ) = θ x θ − 1 I { 0 < x < 1 } X \sim f(x)=\theta x^{\theta-1} I\{0<x<1\} X∼f(x)=θxθ−1I{ 0<x<1} Of n n n Random sample , seek
(1)(5 branch ) θ \theta θ Of M L E , \mathrm{MLE}, MLE, And verify the unbiased ;
(2)(5 branch ) verification MLE The consistency of ;
(3)(5 branch ) θ \theta θ The moment estimate of ;
(4)(5 branch ) Use the sample median pair θ \theta θ Estimate .
7、 ... and 、(20 branch ) X 1 , … , X n , X_{1}, \ldots, X_{n}, X1,…,Xn, i.i.d ∼ N ( μ , σ 2 ) , \sim N\left(\mu, \sigma^{2}\right), ∼N(μ,σ2), prove [ X ( 1 ) , X ( n ) ] \left[X_{(1)}, X_{(n)}\right] [X(1),X(n)] yes μ \mu μ The confidence level of is 1 − 2 1 − n 1-2^{1-n} 1−21−n The confidence interval of .
8、 ... and 、(20 branch ) Some come from the general X ∼ f ( x ) = 1 2 e − ∣ x − θ ∣ X \sim f(x)=\frac{1}{2} e^{-|x-\theta|} X∼f(x)=21e−∣x−θ∣ Of 7 Random sample , seek θ \theta θ Of MLE.
Nine 、(10 branch ) ( X 1 , X 2 ) ∼ N ( 0 , 0 ; 1 , 1 ; 0 ) , (X_1, X_2) \sim N(0,0 ; 1,1 ; 0), (X1,X2)∼N(0,0;1,1;0), seek X 1 X 2 \frac{X_1}{X_2} X2X1 Probability distribution of .
The analysis part
One 、(20 branch ) A family has two children , Find the probability of the following events :
(1)(10 branch ) The first one is known to be a girl , Find the probability that the second is a girl ;
(2)(10 branch ) One is known to be a girl , Find the probability that the other is a girl .
Solution:
(1) First of all, suppose : The probability of a child being a girl without any information is 0.5 0.5 0.5.
In the event A i A_{i} Ai It means the first one i i i This is a girl ( i = 1 , 2 ) (i=1,2) (i=1,2), be P ( A 2 ∣ A 1 ) = P ( A 1 A 2 ) P ( A 1 ) = 0.25 0.5 = 0.5 P\left(A_{2} \mid A_{1}\right)=\frac{P\left(A_{1} A_{2}\right)}{P\left(A_{1}\right)}=\frac{0.25}{0.5}=0.5 P(A2∣A1)=P(A1)P(A1A2)=0.50.25=0.5.
(2) P ( A 1 A 2 ∣ A 1 ∪ A 2 ) = P ( A 1 A 2 ) P ( A 1 ∪ A 2 ) = 0.25 0.75 = 1 3 P\left(A_{1} A_{2} \mid A_{1} \cup A_{2}\right)=\frac{P\left(A_{1} A_{2}\right)}{P\left(A_{1} \cup A_{2}\right)}=\frac{0.25}{0.75}=\frac{1}{3} P(A1A2∣A1∪A2)=P(A1∪A2)P(A1A2)=0.750.25=31.
Two 、(15 branch ) Jiayou 21 A coin , B has 20 A coin , Both of them toss all the coins at the same time , Find the probability that the number of coins with a facing up is more than that of B .
Solution:
According to the symmetry, we can know , P { P\{ P{ There are more coins with a facing up than with B } = P { \}=P\{ }=P{ There are more coins with a side down than with B } \} }. use A random variable X X X Indicates the number of coins with a facing up , A random variable Y Y Y Indicates the number of coins with B facing up . be :
P { X > Y } = P { 21 − X > 20 − Y } = P { 1 − X > − Y } = P { X < Y + 1 } = P { X ⩽ Y } \begin{aligned} P\{X>Y\} &=P\{21-X>20-Y\}=P\{1-X>-Y\} \\ &=P\{X<Y+1\}=P\{X \leqslant Y\} \end{aligned} P{ X>Y}=P{ 21−X>20−Y}=P{ 1−X>−Y}=P{ X<Y+1}=P{ X⩽Y} also P { X > Y } + P { X ⩽ Y } = 1 P\{X>Y\}+P\{X \leqslant Y\}=1 P{ X>Y}+P{ X⩽Y}=1, therefore P { X > Y } = P { X ⩽ Y } = 0.5 P\{X>Y\}=P\{X \leqslant Y\}=0.5 P{ X>Y}=P{ X⩽Y}=0.5.
3、 ... and 、(15 branch ) There are countless parallel lines on the plane , Every two parallel lines are spaced 2 rice , Use side length 1 An equilateral triangle of meters is thrown at the plane , Find the probability of triangle pressing to a straight line .
Solution:
remember △ A B C \triangle A B C △ABC The three sides of the are a , b , c a, b, c a,b,c. Then there are the following situations when a triangle intersects a parallel line :
(1) One vertex of the triangle is on the parallel line ;
(2) One side of the triangle coincides with the straight line ;
(3) Two lines of triangle Edges intersect parallel lines .
According to the geometric probability P ( 1 ) = P ( 2 ) = 0 P(1)=P(2)=0 P(1)=P(2)=0, So just consider the situation (3). and P ( 3 ) = P a b + P a c + P b c P(3)=P_{a b}+P_{a c}+P_{b c} P(3)=Pab+Pac+Pbc, among P a b P_{a b} Pab edge a 、 b a 、 b a、b Intersect with parallel lines . So , remember P a P_{a} Pa edge a a a Intersect with parallel lines , be P a = P a c + P a b P_{a}=P_{a c}+P_{a b} Pa=Pac+Pab. so P ( 3 ) = 1 2 ( P a + P b + P c ) , P(3)=\frac{1}{2}\left(P_{a}+P_{b}+P_{c}\right), P(3)=21(Pa+Pb+Pc), Now we only need to find P a 、 P b 、 P c P_{a} 、 P_{b} 、 P_{c} Pa、Pb、Pc. This is a Buffon Injection model , The probability is P a = 2 a d π P_{a}=\frac{2 a}{d \pi} Pa=dπ2a, among a a a Is the edge a a a The length of , d d d It's parallel Spacing between lines , Substituting data can be calculated P a = 2 2 π = 1 π P_{a}=\frac{2}{2 \pi}=\frac{1}{\pi} Pa=2π2=π1. Empathy P b = P c = 1 π P_{b}=P_{c}=\frac{1}{\pi} Pb=Pc=π1. so
P { Triangle pressed to a straight line } = P ( 3 ) = 1 2 ( P a + P b + P c ) = 3 2 π . P\{\text { Triangle pressed to a straight line }\}=P(3)=\frac{1}{2}\left(P_{a}+P_{b}+P_{c}\right)=\frac{3}{2 \pi}. P{ Triangle pressed to a straight line }=P(3)=21(Pa+Pb+Pc)=2π3.
Four 、(15 branch ) 8 A boy 、7 Two girls sit in a row , set up X i = 1 X_{i}=1 Xi=1 It means the first one i i i The first position is the same as i + 1 i+1 i+1 The opposite sex sits in this position , X i = 0 X_{i}=0 Xi=0 It means the first one i i i The first position is the same as i + 1 i+1 i+1 Sitting in the same seat , ξ = ∑ i = 1 14 X i , \xi=\sum_{i=1}^{14} X_{i}, ξ=∑i=114Xi, seek E ξ . E \xi . Eξ.
Solution:
E ξ = E ( ∑ i = 1 14 X i ) = ∑ i = 1 14 E X i E \xi=E\left(\sum_{i=1}^{14} X_{i}\right)=\sum_{i=1}^{14} E X_{i} Eξ=E(∑i=114Xi)=∑i=114EXi, Considering all X i X_{i} Xi It's identically distributed , Now E X 1 E X_{1} EX1.
E X 1 = P ( X 1 = 1 ) = C 8 1 C 7 1 C 15 2 = 8 × 7 15 × 14 2 × 1 = 8 15 E X_{1}=P\left(X_{1}=1\right)=\frac{C_{8}^{1} C_{7}^{1}}{C_{15}^{2}}=\frac{8 \times 7}{\frac{15 \times 14}{2 \times 1}}=\frac{8}{15} EX1=P(X1=1)=C152C81C71=2×115×148×7=158 therefore E ξ = ∑ i = 1 14 E X i = 14 E X 1 = 112 15 E \xi=\sum_{i=1}^{14} E X_{i}=14 E X_{1}=\frac{112}{15} Eξ=∑i=114EXi=14EX1=15112.
5、 ... and 、(15 branch ) Cite an expectation that tends to be positive and infinite , But it converges to 0 A sequence of random variables { X n } \left\{X_{n}\right\} { Xn}.
Solution:
Give such a sequence of random variables : P ( X n = 0 ) = 1 − 1 n , P ( X n = n 2 ) = 1 n P\left(X_{n}=0\right)=1-\frac{1}{n}, P\left(X_{n}=n^{2}\right)=\frac{1}{n} P(Xn=0)=1−n1,P(Xn=n2)=n1. E X n = n → + ∞ E X_{n}=n \rightarrow+\infty EXn=n→+∞. and P ( X n ≠ 0 ) = 1 n P\left(X_{n} \neq 0\right)=\frac{1}{n} P(Xn=0)=n1, be X n → P 0 X_{n} \stackrel{P}{\rightarrow} 0 Xn→P0.
6、 ... and 、(20 branch ) Some come from the general X ∼ f ( x ) = θ x θ − 1 I { 0 < x < 1 } X \sim f(x)=\theta x^{\theta-1} I\{0<x<1\} X∼f(x)=θxθ−1I{ 0<x<1} Of n n n Random sample , seek
(1)(5 branch ) θ \theta θ Of M L E , \mathrm{MLE}, MLE, And verify the unbiased ;
(2)(5 branch ) verification MLE The consistency of ;
(3)(5 branch ) θ \theta θ The moment estimate of ;
(4)(5 branch ) Use the sample median pair θ \theta θ Estimate .
Solution:
(1) Likelihood function L ( X ; θ ) = θ n ( ∏ i = 1 n x i ) θ − 1 L(\mathbf{X} ; \theta)=\theta^{n}\left(\prod_{i=1}^{n} x_{i}\right)^{\theta-1} L(X;θ)=θn(∏i=1nxi)θ−1, Log likelihood function ln L = n ln θ + ( θ − 1 ) ∑ i = 1 n ln x i \ln L=n \ln \theta+(\theta-1) \sum_{i=1}^{n} \ln x_{i} lnL=nlnθ+(θ−1)∑i=1nlnxi. Make ∂ ln L ∂ θ = n θ + ∑ i = 1 n ln x i = 0 \frac{\partial \ln L}{\partial \theta}=\frac{n}{\theta}+\sum_{i=1}^{n} \ln x_{i}=0 ∂θ∂lnL=θn+∑i=1nlnxi=0, Solution θ ^ L = n ∑ i = 1 n ( − ln x i ) \hat{\theta}_{L}=\frac{n}{\sum_{i=1}^{n}\left(-\ln x_{i}\right)} θ^L=∑i=1n(−lnxi)n. And because the whole obeys beta distribution , Belong to Exponential family distribution , The stationary point of its log likelihood function must be maximum likelihood estimation . therefore θ ^ L = n ∑ i = 1 n ( − ln x i ) \hat{\theta}_{L}=\frac{n}{\sum_{i=1}^{n}\left(-\ln x_{i}\right)} θ^L=∑i=1n(−lnxi)n yes θ \theta θ Maximum likelihood estimation of . If order Y i = − ln X i ∼ Exp ( θ ) Y_{i}=-\ln X_{i} \sim \operatorname{Exp}(\theta) Yi=−lnXi∼Exp(θ), And from the additivity of gamma distribution T = ∑ i = 1 n y i ∼ G a ( n , θ ) T=\sum_{i=1}^{n} y_{i} \sim G a(n, \theta) T=∑i=1nyi∼Ga(n,θ), Zeji Large likelihood estimation can be written as θ ^ L = n T \hat{\theta}_{L}=\frac{n}{T} θ^L=Tn.
E θ ^ L = E n T = ∫ 0 + ∞ n t θ n Γ ( n ) t n − 1 e − θ t d t = n θ Γ ( n ) ∫ 0 + ∞ ( θ t ) n − 2 e − θ t d ( θ t ) = n θ Γ ( n ) Γ ( n − 1 ) = n n − 1 θ E \hat{\theta}_{L}=E \frac{n}{T}=\int_{0}^{+\infty} \frac{n}{t} \frac{\theta^{n}}{\Gamma(n)} t^{n-1} e^{-\theta t} d t=\frac{n \theta}{\Gamma(n)} \int_{0}^{+\infty}(\theta t)^{n-2} e^{-\theta t} d(\theta t)=\frac{n \theta}{\Gamma(n)} \Gamma(n-1)=\frac{n}{n-1} \theta Eθ^L=ETn=∫0+∞tnΓ(n)θntn−1e−θtdt=Γ(n)nθ∫0+∞(θt)n−2e−θtd(θt)=Γ(n)nθΓ(n−1)=n−1nθ
therefore θ ^ L \hat{\theta}_{L} θ^L No θ \theta θ Unbiased estimation of , But it is gradual and unbiased .
(2) In the last question, we have calculated E θ ^ L = n n − 1 θ → θ E \hat{\theta}_{L}=\frac{n}{n-1} \theta \rightarrow \theta Eθ^L=n−1nθ→θ, Now consider its consistency .
E θ ^ L 2 = E n 2 T 2 = n 2 θ 2 Γ ( n ) ∫ 0 + ∞ ( θ t ) n − 3 e − θ t d ( θ t ) = n 2 θ 2 Γ ( n ) Γ ( n − 2 ) = n 2 ( n − 1 ) ( n − 2 ) θ 2 , E \hat{\theta}_{L}^{2}=E \frac{n^{2}}{T^{2}}=\frac{n^{2} \theta^{2}}{\Gamma(n)} \int_{0}^{+\infty}(\theta t)^{n-3} e^{-\theta t} d(\theta t)=\frac{n^{2} \theta^{2}}{\Gamma(n)} \Gamma(n-2)=\frac{n^{2}}{(n-1)(n-2)} \theta^{2}, Eθ^L2=ET2n2=Γ(n)n2θ2∫0+∞(θt)n−3e−θtd(θt)=Γ(n)n2θ2Γ(n−2)=(n−1)(n−2)n2θ2,
be Var ( θ ^ L ) = E θ ^ L 2 − ( E θ ^ L ) 2 = n 2 θ 2 ( n − 1 ) ( n − 2 ) − n 2 θ 2 ( n − 1 ) 2 = n 2 ( n − 1 ) 2 ( n − 2 ) θ 2 \operatorname{Var}\left(\hat{\theta}_{L}\right)=E \hat{\theta}_{L}^{2}-\left(E \hat{\theta}_{L}\right)^{2}=\frac{n^{2} \theta^{2}}{(n-1)(n-2)}-\frac{n^{2} \theta^{2}}{(n-1)^{2}}=\frac{n^{2}}{(n-1)^{2}(n-2)} \theta^{2} Var(θ^L)=Eθ^L2−(Eθ^L)2=(n−1)(n−2)n2θ2−(n−1)2n2θ2=(n−1)2(n−2)n2θ2.
P ( ∣ θ ^ L − θ ∣ ≥ ε ) = P ( ∣ θ ^ L − n n − 1 θ + n n − 1 θ − θ ∣ ≥ ε ) P\left(\left|\hat{\theta}_{L}-\theta\right| \geq \varepsilon\right)=P\left(\left|\hat{\theta}_{L}-\frac{n}{n-1} \theta+\frac{n}{n-1} \theta-\theta\right| \geq \varepsilon\right) P(∣∣∣θ^L−θ∣∣∣≥ε)=P(∣∣∣∣θ^L−n−1nθ+n−1nθ−θ∣∣∣∣≥ε) ≤ P ( ∣ θ ^ L − n n − 1 θ ∣ ≥ ε 2 ) + P ( ∣ n n − 1 θ − θ ∣ ≥ ε 2 ) \leq P\left(\left|\hat{\theta}_{L}-\frac{n}{n-1} \theta\right| \geq \frac{\varepsilon}{2}\right)+P\left(\left|\frac{n}{n-1} \theta-\theta\right| \geq \frac{\varepsilon}{2}\right) ≤P(∣∣∣∣θ^L−n−1nθ∣∣∣∣≥2ε)+P(∣∣∣∣n−1nθ−θ∣∣∣∣≥2ε) According to Chebyshev inequality P ( ∣ θ ^ L − n n − 1 θ ∣ ≥ ε 2 ) ≤ 4 Var ( θ ^ L ) ε 2 = 4 ε 2 n 2 ( n − 1 ) 2 ( n − 2 ) θ 2 → 0 P\left(\left|\hat{\theta}_{L}-\frac{n}{n-1} \theta\right| \geq \frac{\varepsilon}{2}\right) \leq \frac{4 \operatorname{Var}\left(\hat{\theta}_{L}\right)}{\varepsilon^{2}}=\frac{4}{\varepsilon^{2}} \frac{n^{2}}{(n-1)^{2}(n-2)} \theta^{2} \rightarrow 0 P(∣∣∣θ^L−n−1nθ∣∣∣≥2ε)≤ε24Var(θ^L)=ε24(n−1)2(n−2)n2θ2→0 And for the larger n , P ( ∣ n n − 1 θ − θ ∣ ≥ ε 2 ) = 0 n, P\left(\left|\frac{n}{n-1} \theta-\theta\right| \geq \frac{\varepsilon}{2}\right)=0 n,P(∣∣n−1nθ−θ∣∣≥2ε)=0. therefore P ( ∣ θ ^ L − θ ∣ ≥ ε ) → 0 P\left(\left|\hat{\theta}_{L}-\theta\right| \geq \varepsilon\right) \rightarrow 0 P(∣∣∣θ^L−θ∣∣∣≥ε)→0, in other words θ ^ L \hat{\theta}_{L} θ^L yes θ \theta θ A consistent estimate of .
(3) Overall obedience Beta ( θ , 1 ) \operatorname{Beta}(\theta, 1) Beta(θ,1), Digital features distributed by beta , We know E X = θ θ + 1 E X=\frac{\theta}{\theta+1} EX=θ+1θ. According to the inverse solution θ \theta θ The moment estimate of θ ^ M = x ˉ 1 − x ˉ \hat{\theta}_{M}=\frac{\bar{x}}{1-\bar{x}} θ^M=1−xˉxˉ.
(4) The overall distribution function is F ( x ) = { 0 , x < 0 x θ , 0 ≤ x < 1 1 , x ≥ 1 F(x)=\left\{\begin{array}{cc}0, & x<0 \\ x^{\theta}, & 0 \leq x<1 \\ 1, & x \geq 1\end{array}\right. F(x)=⎩⎨⎧0,xθ,1,x<00≤x<1x≥1 Make F ( x ) = 1 2 F(x)=\frac{1}{2} F(x)=21, Solution x 0.5 = ( 1 2 ) 1 θ x_{0.5}=\left(\frac{1}{2}\right)^{\frac{1}{\theta}} x0.5=(21)θ1, Use the median of the sample m 0.5 m_{0.5} m0.5 Replace the overall median x 0.5 x_{0.5} x0.5, And inverse solution Out θ ^ = 1 log 1 2 m 0.5 = log 1 2 1 2 log 1 2 m 0.5 = log m 0.5 1 2 \hat{\theta}=\frac{1}{\log _{\frac{1}{2}} m_{0.5}}=\frac{\log _{\frac{1}{2}} \frac{1}{2}}{\log _{\frac{1}{2}} m_{0.5}}=\log _{m_{0.5}} \frac{1}{2} θ^=log21m0.51=log21m0.5log2121=logm0.521 It is based on the median pair of samples θ \theta θ Estimation .
7、 ... and 、(20 branch ) X 1 , … , X n , X_{1}, \ldots, X_{n}, X1,…,Xn, i.i.d ∼ N ( μ , σ 2 ) , \sim N\left(\mu, \sigma^{2}\right), ∼N(μ,σ2), prove [ X ( 1 ) , X ( n ) ] \left[X_{(1)}, X_{(n)}\right] [X(1),X(n)] yes μ \mu μ The confidence level of is 1 − 2 1 − n 1-2^{1-n} 1−21−n The confidence interval of .
Solution:
First consider asking U = x ( 1 ) U=x_{(1)} U=x(1) The distribution of , According to the calculation formula of the minimum value distribution
F U ( u ) = 1 − [ 1 − Φ ( u − μ σ ) ] n F_{U}(u)=1-\left[1-\Phi\left(\frac{u-\mu}{\sigma}\right)\right]^{n} FU(u)=1−[1−Φ(σu−μ)]n be P ( μ < x ( 1 ) ) = 1 − F U ( μ ) = [ 1 − Φ ( 0 ) ] n = ( 1 2 ) n = 2 − n P\left(\mu<x_{(1)}\right)=1-F_{U}(\mu)=[1-\Phi(0)]^{n}=\left(\frac{1}{2}\right)^{n}=2^{-n} P(μ<x(1))=1−FU(μ)=[1−Φ(0)]n=(21)n=2−n.
According to the symmetry P ( μ > x ( n ) ) = 2 − n P\left(\mu>x_{(n)}\right)=2^{-n} P(μ>x(n))=2−n. therefore P ( x ( 1 ) ⩽ μ ⩽ x ( n ) ) = 1 − 2 ⋅ 2 − n = 1 − 2 1 − n P\left(x_{(1)} \leqslant \mu \leqslant x_{(n)}\right)=1-2 \cdot 2^{-n}=1-2^{1-n} P(x(1)⩽μ⩽x(n))=1−2⋅2−n=1−21−n
8、 ... and 、(20 branch ) Some come from the general X ∼ f ( x ) = 1 2 e − ∣ x − θ ∣ X \sim f(x)=\frac{1}{2} e^{-|x-\theta|} X∼f(x)=21e−∣x−θ∣ Of 7 Random sample , seek θ \theta θ Of MLE.
Solution:
Likelihood function L ( X ; θ ) = ( 1 2 ) 7 e − ∑ i = 1 7 ∣ x i − θ ∣ = ( 1 2 ) 7 e − ∑ i = 1 7 ∣ x ( i ) − θ ∣ L(\mathbf{X} ; \theta)=\left(\frac{1}{2}\right)^{7} e^{-\sum_{i=1}^{7}\left|x_{i}-\theta\right|}=\left(\frac{1}{2}\right)^{7} e^{-\sum_{i=1}^{7}\left|x_{(i)}-\theta\right|} L(X;θ)=(21)7e−∑i=17∣xi−θ∣=(21)7e−∑i=17∣x(i)−θ∣. here x ( i ) x_{(i)} x(i) It means No i i i Order statistics . In order to make the likelihood function as large as possible , Should make e − ∑ i = 1 7 ∣ x ( 0 ) − θ ∣ e^{-\sum_{i=1}^{7}\left|x_{(0)}-\theta\right|} e−∑i=17∣x(0)−θ∣ As big as possible , That is to make ∑ i = 1 7 ∣ x ( i ) − θ ∣ \sum_{i=1}^{7}\left|x_{(i)}-\theta\right| ∑i=17∣∣x(i)−θ∣∣ As small as possible . The following research ∑ i = 1 7 ∣ x ( i ) − θ ∣ \sum_{i=1}^{7}\left|x_{(i)}-\theta\right| ∑i=17∣∣x(i)−θ∣∣ The state of being :
∑ i = 1 7 ∣ x ( i ) − θ ∣ = ∑ i = 1 3 ( ∣ x ( i ) − θ ∣ + ∣ x ( 7 − i + 1 ) − θ ∣ ) + ∣ x ( 4 ) − θ ∣ \sum_{i=1}^{7}\left|x_{(i)}-\theta\right|=\sum_{i=1}^{3}\left(\left|x_{(i)}-\theta\right|+\left|x_{(7-i+1)}-\theta\right|\right)+\left|x_{(4)}-\theta\right| i=1∑7∣∣x(i)−θ∣∣=i=1∑3(∣∣x(i)−θ∣∣+∣∣x(7−i+1)−θ∣∣)+∣∣x(4)−θ∣∣ ( The above formula will x ( 1 ) , x ( 7 ) x_{(1)}, x_{(7)} x(1),x(7) Divided into one group , x ( 2 ) , x ( 6 ) x_{(2)}, x_{(6)} x(2),x(6) Divided into one group , x ( 3 ) , x ( 5 ) x_{(3)}, x_{(5)} x(3),x(5) Divided into one group , x ( 4 ) x_{(4)} x(4) A single group )
among ∣ x ( i ) − θ ∣ + ∣ x ( 7 − i + 1 ) − θ ∣ \left|x_{(i)}-\theta\right|+\left|x_{(7-i+1)}-\theta\right| ∣∣x(i)−θ∣∣+∣∣x(7−i+1)−θ∣∣ stay θ ∈ [ x ( i ) , x ( 7 − i + 1 ) ] \theta \in\left[x_{(i)}, x_{(7-i+1)}\right] θ∈[x(i),x(7−i+1)] Take the minimum value when ; ∣ x ( 4 ) − θ ∣ \left|x_{(4)}-\theta\right| ∣∣x(4)−θ∣∣ stay θ = x ( 4 ) \theta=x_{(4)} θ=x(4) Take the minimum value when . and ( ⋂ i = 1 3 [ x ( i ) , x ( 7 − i + 1 ) ] ) ∩ { x ( 4 ) } = { x ( 4 ) } \left(\bigcap_{i=1}^{3}\left[x_{(i)}, x_{(7-i+1)}\right]\right) \cap\left\{x_{(4)}\right\}=\left\{x_{(4)}\right\} (⋂i=13[x(i),x(7−i+1)])∩{ x(4)}={ x(4)}, therefore θ ^ = x ( 4 ) \hat{\theta}=x_{(4)} θ^=x(4) yes θ \theta θ Of MLE.
Nine 、(10 branch ) ( X 1 , X 2 ) ∼ N ( 0 , 0 ; 1 , 1 ; 0 ) , (X_1, X_2) \sim N(0,0 ; 1,1 ; 0), (X1,X2)∼N(0,0;1,1;0), seek X 1 X 2 \frac{X_1}{X_2} X2X1 Probability distribution of .
Solution:
Due to denominator X 2 X_{2} X2 The distribution of is about 0 symmetry , therefore X 1 ∣ X 2 ∣ \frac{X_{1}}{\left|X_{2}\right|} ∣X2∣X1 And X 1 X 2 \frac{X_{1}}{X_{2}} X2X1 Homodistribution , And obviously N ( 0 , 1 ) χ 2 ( 1 ) 1 \frac{N(0,1)}{\sqrt{\frac{\chi^{2}(1)}{1}}} 1χ2(1)N(0,1) It's a The degree of freedom is 1 Of t t t Distribution , therefore X 1 ∣ X 2 ∣ \frac{X_{1}}{\left|X_{2}\right|} ∣X2∣X1 Also, the degree of freedom is 1 Of t t t Distribution , Its probability density is f ( x ) = Γ ( 1 ) π Γ ( 1 2 ) ( x 2 + 1 ) − 1 = 1 π ⋅ 1 1 + x 2 , − ∞ < x < + ∞ , f(x)=\frac{\Gamma(1)}{\sqrt{\pi} \Gamma\left(\frac{1}{2}\right)}\left(x^{2}+1\right)^{-1}=\frac{1}{\pi} \cdot \frac{1}{1+x^{2}},-\infty<x<+\infty, f(x)=πΓ(21)Γ(1)(x2+1)−1=π1⋅1+x21,−∞<x<+∞, The standard Cauchy distribution .
边栏推荐
- View UI Plus 發布 1.3.1 版本,增强 TypeScript 使用體驗
- 2.C语言初阶练习题(2)
- View UI Plus 发布 1.3.1 版本,增强 TypeScript 使用体验
- View UI plus released version 1.3.0, adding space and $imagepreview components
- Arduino+ds18b20 temperature sensor (buzzer alarm) +lcd1602 display (IIC drive)
- 西安电子科技大学22学年上学期《射频电路基础》试题及答案
- 1. C language matrix addition and subtraction method
- Solution: warning:tensorflow:gradients do not exist for variables ['deny_1/kernel:0', 'deny_1/bias:0',
- Redis的两种持久化机制RDB和AOF的原理和优缺点
- 3. C language uses algebraic cofactor to calculate determinant
猜你喜欢

TYUT太原理工大学2022“mao gai”必背

Cloud native trend in 2022
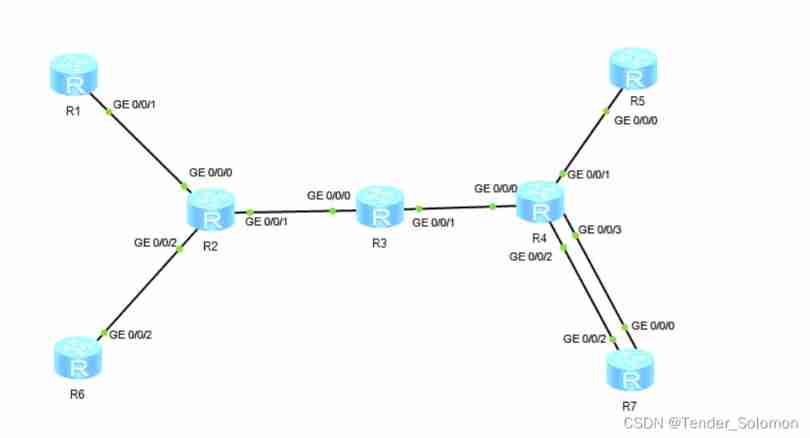
MPLS experiment

Tyut Taiyuan University of technology 2022 introduction to software engineering summary
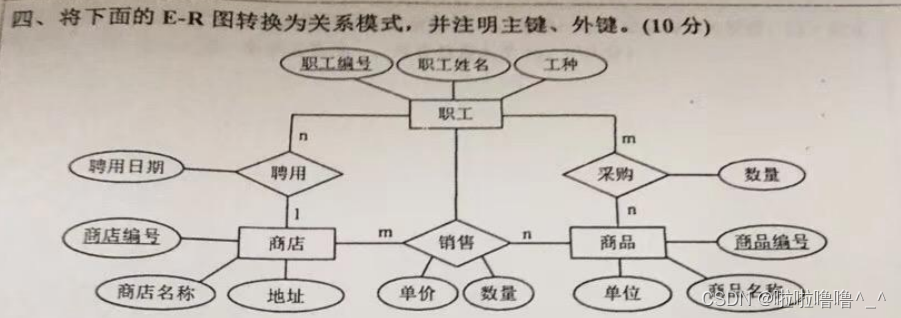
TYUT太原理工大学2022数据库大题之E-R图转关系模式

这次,彻底搞清楚MySQL索引

C language to achieve mine sweeping game (full version)
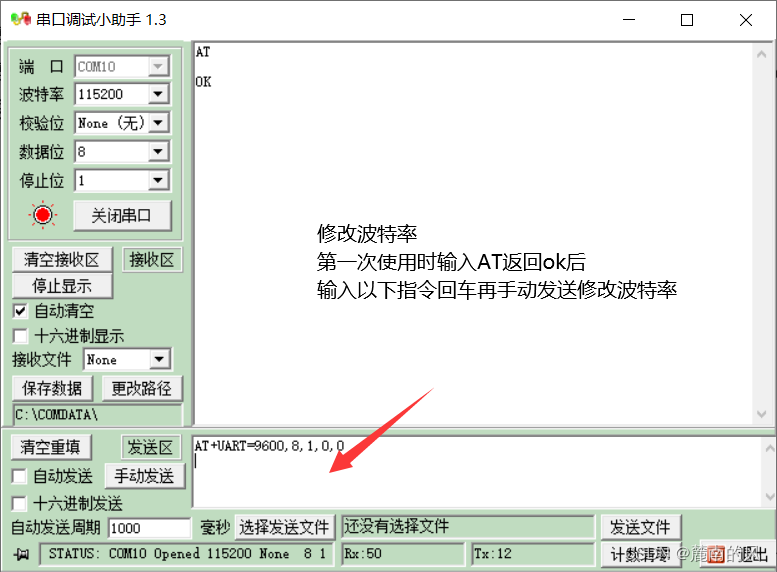
(超详细onenet TCP协议接入)arduino+esp8266-01s接入物联网平台,上传实时采集数据/TCP透传(以及lua脚本如何获取和编写)
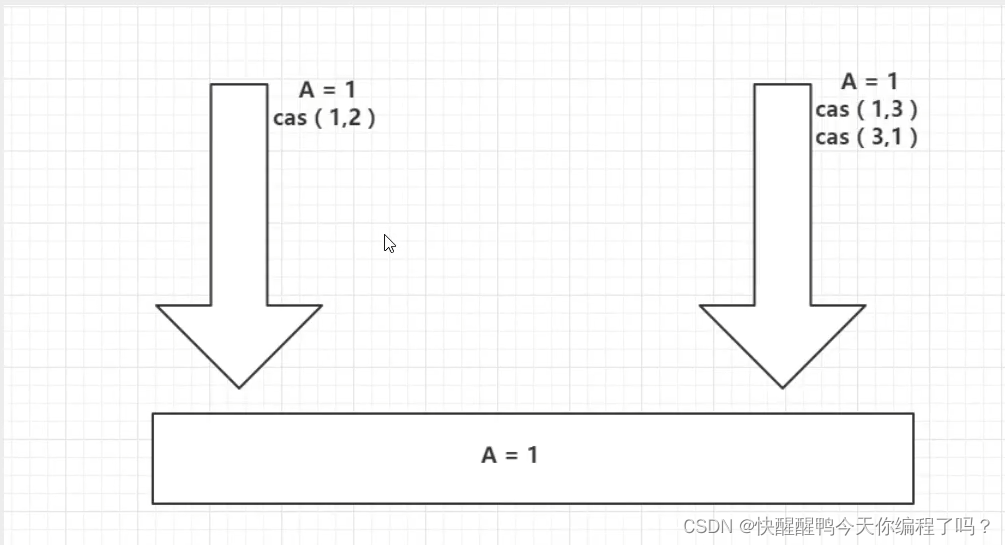
ABA问题遇到过吗,详细说以下,如何避免ABA问题

5.MSDN的下载和使用
随机推荐
5. Function recursion exercise
学编程的八大电脑操作,总有一款你不会
【快趁你舍友打游戏,来看道题吧】
3. C language uses algebraic cofactor to calculate determinant
ABA问题遇到过吗,详细说以下,如何避免ABA问题
Alibaba cloud microservices (IV) service mesh overview and instance istio
View UI plus released version 1.3.1 to enhance the experience of typescript
Tyut Taiyuan University of technology 2022 "Mao Gai" must be recited
List set map queue deque stack
fianl、finally、finalize三者的区别
MPLS experiment
为什么要使用Redis
[while your roommate plays games, let's see a problem]
4.分支语句和循环语句
甲、乙机之间采用方式 1 双向串行通信,具体要求如下: (1)甲机的 k1 按键可通过串行口控制乙机的 LEDI 点亮、LED2 灭,甲机的 k2 按键控制 乙机的 LED1
Cloud native trend in 2022
Share a website to improve your Aesthetics
5月14日杂谈
Alibaba cloud microservices (I) service registry Nacos, rest template and feign client
4.二分查找