当前位置:网站首页>The 19th Zhejiang Provincial Collegiate Programming Contest 2022浙江省赛 F.EasyFix 主席树
The 19th Zhejiang Provincial Collegiate Programming Contest 2022浙江省赛 F.EasyFix 主席树
2022-07-07 21:50:00 【HeartFireY】
F.Easy Fix
题目分析
给定排列 p 1 , p 2 , p 3 , … , p n p_1, p_2, p_3,\dots, p_n p1,p2,p3,…,pn,定义 A i A_i Ai表示在 p i p_i pi左侧并比 p i p_i pi小的数字个数, B i B_i Bi表示在 p i p_i pi右侧并比 p i p_i pi小的数字个数, C i = min ( A i , B i ) C_i = \min(A_i, B_i) Ci=min(Ai,Bi)。现在给定多个操作 ( l , r ) (l, r) (l,r),求每个操作,交换 ( p i , p j ) (p_i, p_j) (pi,pj)后的 ∑ C i \sum C_i ∑Ci。
首先考虑如何处理初始时的 C i C_i Ci值,观察到以下性质:
- 对于 A i A_i Ai值的求解过程类似求逆序对的思想,可以直接上树状数组维护, O ( n log n ) O(n\log n) O(nlogn)求得全部的 A i A_i Ai
- 由于是排列, B i = p i − 1 − A i B_i = p_i - 1 - A_i Bi=pi−1−Ai可以 O ( 1 ) O(1) O(1)求得
- 那么 C i = min ( A i , B i ) C_i = \min(A_i, B_i) Ci=min(Ai,Bi)也是 O ( 1 ) O(1) O(1)得到的
由于每个询问相互独立,那么考虑交换 ( p l , p r ) (p_l, p_r) (pl,pr)操作对 C i C_i Ci的影响:
对于 [ 1 , l ) , ( r , n ] [1, l), (r , n] [1,l),(r,n]范围的数字, C i C_i Ci值一定不影响。因为交换操作均在单侧进行
对于 p l p_l pl,交换到 r r r位置后, A l → A l + 区 间 [ l , r ] 小 于 p l 的 数 字 个 数 A_l \rightarrow A_l + 区间[l,r]小于p_l的数字个数 Al→Al+区间[l,r]小于pl的数字个数, B l ’ B_l’ Bl’仍然可以直接求
对于 p r p_r pr,交换到 l l l位置后, A r → A r − 区 间 [ l , r ] 小 于 p r 的 数 字 个 数 A_r \rightarrow A_r - 区间[l ,r]小于p_r的数字个数 Ar→Ar−区间[l,r]小于pr的数字个数, B r ’ B_r’ Br’仍然可以直接求
如果我们在线询问(主席树维护),那么对于 p l , p r p_l,p_r pl,pr,实际上可以直接两个 O ( l o g n ) O(logn) O(logn)重新求。
那么重点是对于 [ l + 1 , r − 1 ] [l + 1, r - 1] [l+1,r−1]区间内的数字的 C i C_i Ci值变化,如何维护?
对于 p l ≤ p i ≤ p r p_l \leq p_i \leq p_r pl≤pi≤pr,如果 A i ≤ B i A_i \leq B_i Ai≤Bi,则交换后 A i − 1 , B i + 1 A_i - 1, B_i + 1 Ai−1,Bi+1,从而 C i − 1 C_i - 1 Ci−1
对于 p l ≥ p i ≥ p r p_l \geq p_i \geq p_r pl≥pi≥pr,如果 A i ≥ B i A_i \geq B_i Ai≥Bi,则交换后 A i + 1 , B i − 1 A_i + 1, B_i - 1 Ai+1,Bi−1,从而 C i − 1 C_i -1 Ci−1
对于 p l ≤ p i ≤ p r p_l \leq p_i \leq p_r pl≤pi≤pr,如果 A i − 1 ≥ B i + 1 , A i ≥ B i A_i - 1 \geq B_i + 1, A_i \geq B_i Ai−1≥Bi+1,Ai≥Bi,则交换后 C i + 1 C_i + 1 Ci+1
对于 p l ≥ p i ≥ p r p_l \geq p_i \geq p_r pl≥pi≥pr,如果 A i − 1 ≤ B i + 1 , A i ≤ B i A_i - 1 \leq B_i + 1, A_i \leq B_i Ai−1≤Bi+1,Ai≤Bi,则交换后 C i + 1 C_i + 1 Ci+1
那么对于以上四种情况,我们可以分别用四棵主席树进行维护。同时,对于 p l , p r p_l, p_r pl,pr的贡献计算还需要支持区间 < K <K <K的数字个数查询,因此共需五棵主席树进行维护,复杂度 O ( m × 4 log n ) O(m \times 4 \log n) O(m×4logn)。
Code
#include <bits/stdc++.h>
#define int long long
#define endl '\n'
const int N = 1e5 + 10;
int p[N], a[N], b[N], c[N], d[N];
using bset5 = std::bitset<5>;
namespace Fenwick{
int tree[N], len;
#define lowbit(x) ((x) & (-x))
inline void init(int ln){
len = ln; }
inline void update(int i, int x){
for(int pos = i; pos <= len; pos += lowbit(pos)) tree[pos] += x; }
inline int getsum(int i, int ans = 0){
for(int pos = i; pos; pos -= lowbit(pos)) ans += tree[pos]; return ans; }
}
namespace PresidentTree{
int root[N], sum[N << 5][5], lc[N << 5], rc[N << 5], cnt;
#define ls l, mid
#define rs mid + 1, r
void update(int &rt, int pre, int l, int r, int x, bset5 inc){
rt = ++cnt, lc[rt] = lc[pre], rc[rt] = rc[pre];
for(int i = 0; i <= 5; i++) sum[rt][i] = sum[pre][i] + (inc[i] ? 1 : 0);
if(l == r) return;
int mid = l + r >> 1;
if(x <= mid) update(lc[rt], lc[rt], l, mid, x, inc);
else update(rc[rt], rc[rt], mid + 1, r, x, inc);
}
int query(int st, int ed, int l, int r, int L, int R, int id){
if(l == L && r == R) return sum[ed][id] - sum[st][id];
int mid = l + r >> 1;
if(mid >= R) return query(lc[st], lc[ed], l, mid, L, R, id);
else if(mid >= L) return query(lc[st], lc[ed], l, mid, L, mid, id) + query(rc[st], rc[ed], mid + 1, r, mid + 1, R, id);
else return query(rc[st], rc[ed], mid + 1, r, L, R, id);
}
}
#define Pdt PresidentTree
inline void solve(){
int n = 0; std::cin >> n;
Fenwick::init(n);
for(int i = 1; i <= n; i++) std::cin >> p[i];
for(int i = 1; i <= n; i++){
a[i] = Fenwick::getsum(p[i]);
b[i]= p[i] - 1 - a[i];
Fenwick::update(p[i], 1);
c[i] = std::min(a[i], b[i]);
d[i] = d[i - 1] + c[i];
}
for(int i = 1; i <= n; i++){
bset5 flag; flag.reset();
if(a[i] <= b[i]) flag[1] = true;
if(a[i] >= b[i]) flag[3] = true;
if(a[i] - 1 >= b[i] + 1 && a[i] >= b[i]) flag[2] = true;
if(a[i] + 1 <= b[i] - 1 && a[i] <= b[i]) flag[4] = true;
flag[0] = true;
Pdt::update(Pdt::root[i], Pdt::root[i - 1], 1, n + 1, p[i], flag);
}
int m = 0; std::cin >> m;
while(m--){
int l, r; std::cin >> l >> r;
if(l == r){
std::cout << d[n] << endl; continue; }
else if(l > r) std::swap(l, r);
int ans = d[n] - c[l] - c[r];
if(p[l] < p[r]){
ans -= Pdt::query(Pdt::root[l], Pdt::root[r - 1], 1, n + 1, p[l], p[r], 1)
- Pdt::query(Pdt::root[l], Pdt::root[r - 1], 1, n + 1, p[l], p[r], 2);
} else {
ans -= Pdt::query(Pdt::root[l], Pdt::root[r - 1], 1, n + 1, p[r], p[l], 3)
- Pdt::query(Pdt::root[l], Pdt::root[r - 1], 1, n + 1, p[r], p[l], 4);
}
int nowa = Pdt::query(Pdt::root[0], Pdt::root[l - 1], 1, n + 1, 1, p[r], 0),
nowb = p[r] - 1 - nowa;
ans += std::min(nowa, nowb);
nowa = Pdt::query(Pdt::root[r], Pdt::root[n], 1, n + 1, 1, p[l], 0),
nowb = p[l] - 1 - nowa;
ans += std::min(nowa, nowb);
std::cout << ans << endl;
}
}
signed main(){
std::ios_base::sync_with_stdio(false), std::cin.tie(0);
solve();
return 0;
}
边栏推荐
- Comparison of various development methods of applets - cross end? Low code? Native? Or cloud development?
- Binary tree
- 智慧社區和智慧城市之間有什麼异同
- One question per day - pat grade B 1002 questions
- 微信论坛交流小程序系统毕业设计毕设(2)小程序功能
- 2021-01-11
- JMeter interface automated test read case, execute and write back result
- Use JfreeChart to generate curves, histograms, pie charts, and distribution charts and display them to JSP-1
- 微信论坛交流小程序系统毕业设计毕设(8)毕业设计论文模板
- Bit operation
猜你喜欢
Software test classification

DTC社群运营怎么做?
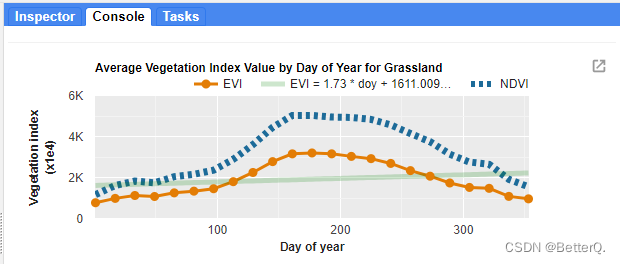
Gee (IV): calculate the correlation between two variables (images) and draw a scatter diagram
【微服务|SCG】gateway整合sentinel

Online interview, how to better express yourself? In this way, the passing rate will be increased by 50%~

Inftnews | the wide application of NFT technology and its existing problems

Unity3D学习笔记6——GPU实例化(1)
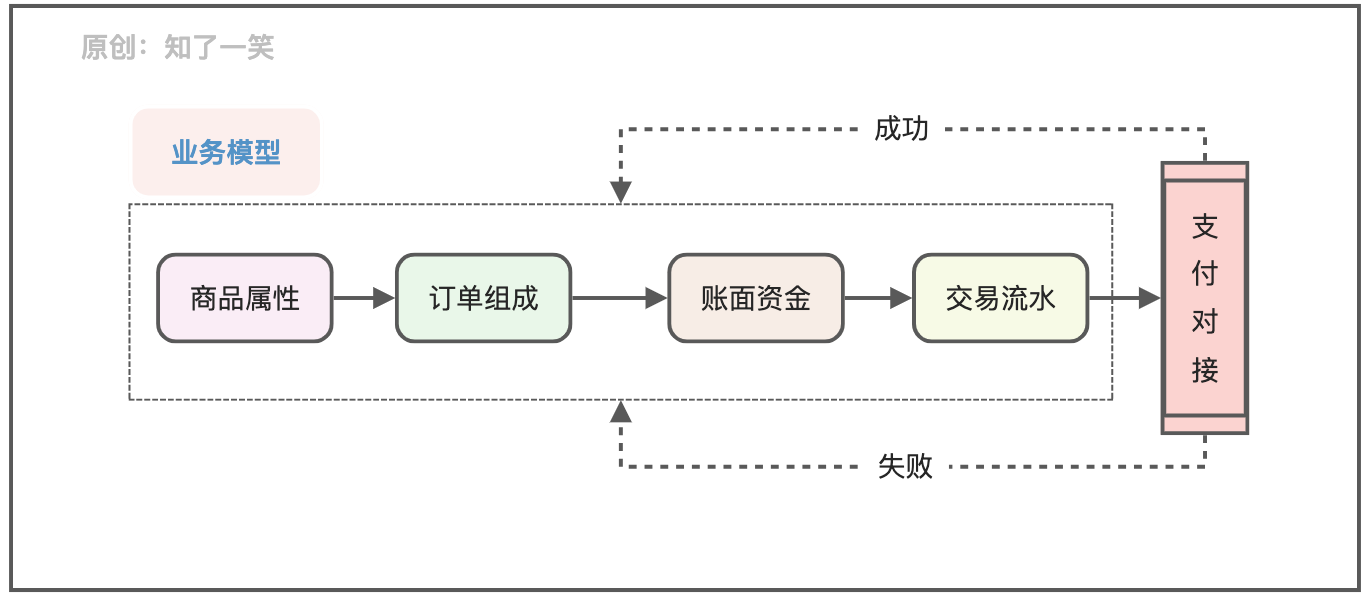
Talk about the design and implementation logic of payment process
leetcode-520. 检测大写字母-js
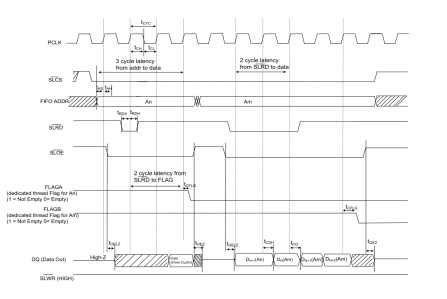
USB(十五)2022-04-14
随机推荐
2021-01-12
Use JfreeChart to generate curves, histograms, pie charts, and distribution charts and display them to jsp-2
USB (十七)2022-04-15
消息队列与快递柜之间妙不可言的关系
kubernetes的简单化数据存储StorageClass(建立和删除以及初步使用)
Bea-3xxxxx error code
Network security - install CentOS
ArcGIS:字段赋值_属性表字段计算器(Field Calculator)依据条件为字段赋值
三菱PLC slmp(mc)协议
Talk about DART's null safety feature
2021-01-11
Network security - information query of operating system
Bit operation
今日创见|企业促进创新的5大关键要素
微信论坛交流小程序系统毕业设计毕设(2)小程序功能
Some parameters of Haikang IPC
Understand the session, cookie and token at one time, and the interview questions are all finalized
Binary tree
数据库每日一题---第22天:最后一次登录
Advantages and disadvantages of rest ful API