当前位置:网站首页>Magic fast power
Magic fast power
2022-07-07 23:44:00 【sophilex】

Ideas ;
Pure simulation is definitely a gift , There are many people who are looking for rules , Find the circular section and then pass .
I saw a show on the Internet and turned my thoughts : Treat an infection process as a multiplication operation , The operation object is the tag array , I've been through so much k operations , That is, take k Time , This is a fast power of deformation
Then just click on the fast power
The overall complexity is about m^2*log(k),4e7 The level of , Theoretically, it can pass
but, Time is still dead ( Maybe the constant is a little big ), You have to add all the miscellaneous optimizations : Fast reading ,register,inline...
Optimized to the extreme , To live through ...( Personal experience )
Although but , This idea is really the first time I have seen , Very good
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define lowbit(x) x&(-x)
const int N=1500;
ll k;
int m,n;
inline ll read() {
register char ch;
while(!isdigit(ch=getchar()));
register ll x=ch^'0';
while(isdigit(ch=getchar())) x=(((x<<2)+x)<<1)+(ch^'0');
return x;
}
bool mas[N],tp[N],ans[N];
inline void mul(bool a[],bool b[])
{
memset(tp,0,sizeof tp);
for(register int i=0;i<m;++i)
{
for(register int j=0;j<m;++j)
{
tp[i*j%m]|=a[i]&&b[j];
}
}
std::copy(&tp[0],&tp[m],a);
}
int main()
{//ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
k=read();m=read();n=read();
for(register int i=1;i<=n;++i)
{
//a=read();
mas[read()]=1;
}
ans[1]=1;
while(k)
{
if(k&1) mul(ans,mas);
mul(mas,mas);
k>>=1;
}
for(register int i=0;i<m;++i) if(ans[i]) printf("%d ",i);
return 0;
}边栏推荐
- 解析token的网址
- Chisel tutorial - 02 Chisel environment configuration and implementation and testing of the first chisel module
- Get started with mongodb
- go time包常用函数
- Dependency injection
- SAP HR social work experience 0023
- Come on, brother
- C inheritance and interface design polymorphism
- Dependency injection 2 advantage lifecycle
- Class C design questions
猜你喜欢
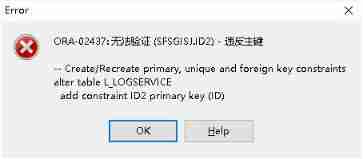
Ora-02437 failed to verify the primary key violation
蓝桥ROS中使用fishros一键安装

AITM3.0005 烟雾毒性测试
Learn about scratch
Pycharm basic settings latest version 2022
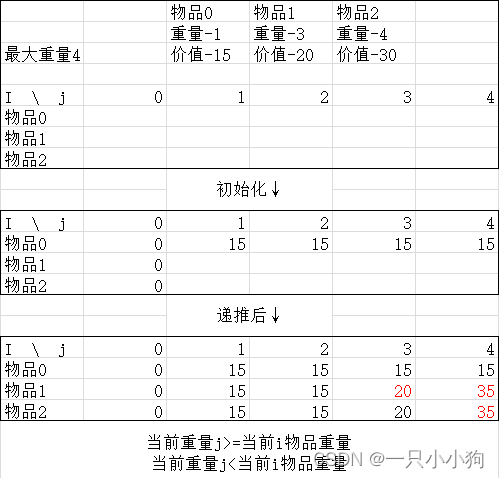
0-1 knapsack problem

Idea automatically generates serialVersionUID
![Balanced binary tree [AVL tree] - insert, delete](/img/1f/cd38b7c6f00f2b3e85d4560181a9d2.png)
Balanced binary tree [AVL tree] - insert, delete
![Arbre binaire équilibré [Arbre AVL] - Insérer et supprimer](/img/1f/cd38b7c6f00f2b3e85d4560181a9d2.png)
Arbre binaire équilibré [Arbre AVL] - Insérer et supprimer

Lm12 rolling heikin Ashi double K-line filter
随机推荐
Enumeration, simulation, and sorting
mysql8.0 ubuntu20.4
UIC564-2 附录4 –阻燃防火测试:火焰的扩散
Display the server hard disk image to the browser through Servlet
Ora-02437 failed to verify the primary key violation
P1067 [noip2009 popularity group] polynomial output (difficult, pit)
神奇快速幂
Understand TCP's three handshakes and four waves with love
受限线性表
Installing gradle
Anti climbing means cracking the second
Markdown
postgis学习
8.31 Tencent interview
SAP HR 社会工作经历 0023
SAP HR labor contract information 0016
Where are you going
MP4文件格式解析之结合实例分析
How can we make money by making video clips from our media?
Anxinco esp32-a1s development board is adapted to Baidu dueros routine to realize online voice function