当前位置:网站首页>【学习笔记】反向误差传播之数值微分
【学习笔记】反向误差传播之数值微分
2022-07-02 06:26:00 【寂云萧】
所谓数值微分,其实说白了就是求导,求导有直接求导和求偏导,在神经网络中用到的一般都是求偏导,从而得到每一个权值的误差。
这次准备用Python来研究一波数值微分。
直接求导
具体求导公式,学过高数应该知道有一个叫“向前差分”的玩意儿,他的公式长这样: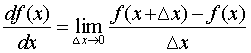
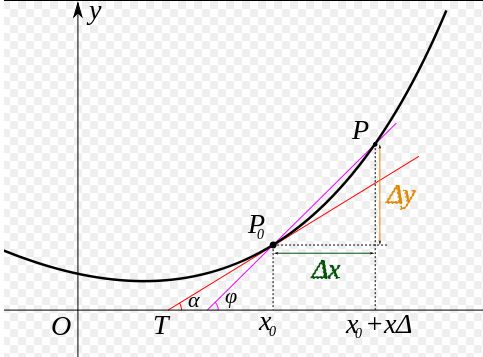
然而在Python中其实并不好实现,因为在这个定义中,向前差分的步长越小越好,但是在Pyhton中小数点并不会保留那么多。所以在小到一定程度的时候就变成了0。
因此一般用“中心差分”,就是x向前加一个步长,向后减一个步长,于是变成了: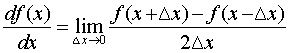
其结果和上面那个是一样的,下面我们可以用Python敲一波代码实现看一下。
#求导函数
#向前差分
def forward_diff(f,x,h=1e-4):
return (f(x+h)-f(x))/h
#中心差分
def diff(f,x,h=1e-4):
return (f(x+h)-f(x-h))/(2*h)
#定义一个函数:y=x^2
def fun(x):
return x**2
x = np.arange(0,4,0.01)
f = fun(x)
#函数在(2,4)处的倒数
dy = diff(fun,2)
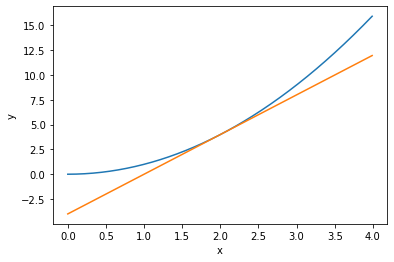
plt.plot(x,f)
#利用直线的公式画出切线
plt.plot(x,dy*(x-2)+4)
plt.xlabel('x')
plt.ylabel('y')
plt.show()
偏导与梯度
上面只是开胃菜,下面才是正题,那就是函数求偏导。这个梯度也是我们在学函数求偏导的时候接触过的一个概念。
如果还有印象,就知道求偏导的时候就是一个函数,比方说下面这个: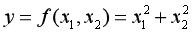
在这个公式当中出现了两个自变量,所以上面的求导公式就不太好使了。因为那个公式只适用于一个自变量的情况下。不过也不是完全不能用,那就是,对于一个自变量求导的时候,就把另一个看作常数处理。这个就是我们在学高数时候的求偏导。而梯度就是由偏导数形成的向量,表现形式如下: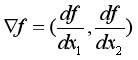
所以梯度是一个向量,他指向的是函数的最低处,也就是最小值。上面的函数有三个个变量,所以有三个坐标轴。因此显示的图像是三维的图像。所以我们可以想象,地面出现凹进去的一块,那么梯度就是指向凹进去的最低处。
学过地理都知道等高线的概念,所以上面的图变化成等高线就是这样,梯度就是指向中心的最低点。就好像我们小时候玩玻璃珠,靠近中间的洞口的时候,玻璃珠自然就会滑到那个洞的最低点。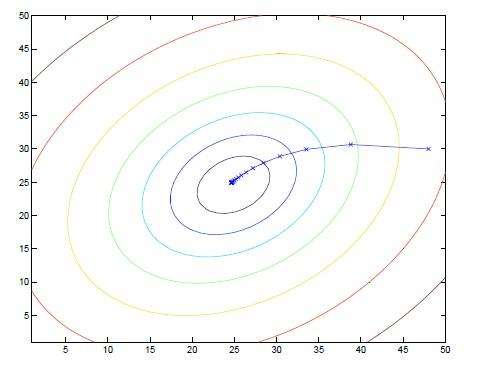
下面老规矩,还是用Python的代码来看。
def gradient(f,x,h=1e-4):
#梯度计算
grad = np.zeros_like(x)
for idx in range(x.size):
tmp_val = x[idx]
x[idx] = tmp_val + h
fxh1 = f(x)
x[idx] = tmp_val - h
fxh2 = f(x)
grad[idx] = (fxh1-fxh2)/(2*h)
x[idx] = tmp_val
return grad
到这里先不要急,我们再学一个机器学习中最经典的算法,那就是梯度下降法,然后我们再来看效果。
梯度下降法
说到梯度下降法这个可就经典了,虽说不是最好的算法,但却是最实用的,也是最简单的,他的存在就是为了找到一个叫做“全局最优解”的东西。不过事与愿违,其实很多时候他会困在“局部最优解”的地方。还是我们玩玻璃珠的例子,玻璃珠在地面滚向洞口的时候,结果刚好路途中还有一个小小的凹洞,于是玻璃珠受重力影响就划进去出不来了,最终是没有达到你想要的那个洞。
这个时候其实就是因为不管是什么洞口,在最低端其实梯度都为0,当梯度为0的时候,就默认以为是到达最优解的地方。
所以具体算法其实很简单。首先我们有一个初始化的坐标,也就是最初玻璃珠的所在地,然后我们求他的梯度值,得到一个指向地面最低处的向量。然后玻璃珠就可以滚过去了(这里绝对不是在骂人)。不过滚过去的时候,肯定不可能一次性滚过去,他存在一个“步长”。就好像我们人走路一样,走向目的地肯定是一步一步的走的,并不能直接飞过去,一步到位。因此我们在这里也设置了一个叫做“学习率”的东西。因此可以得到一次计算更新的值。
下面就是鸡动人心的代码时刻了,我们用Python画一个图,并且记录下每次更新的坐标,然后显示出来。
#最小梯度法函数
def grad_desc(f,init_x,lr=0.01,step=100):
x = init_x
x_history = [] #记录历史坐标值
for i in range(step):
x_history.append( x.copy() ) #使用numpy的copy函数,而不是直接等于
grad = gradient(f,x)
x -= lr*grad
return x,np.array(x_history)
#定义一个函数y=x1^2+x2^2
def fun1(x):
return x[0]**2+x[1]**2
#初始化的坐标
init_x = np.array([-3.0,4.0])
lr = 0.1 #上面默认是0.01,这里可以重新赋值
step = 20 #默认是100,这里重新赋值
x,x_history = grad_desc(fun1,init_x,lr=lr,step=step)
#绘制一个坐标
plt.plot( [-5, 5], [0,0], '--b')
plt.plot( [0,0], [-5, 5], '--b')
#绘制更新的散点
plt.plot(x_history[:,0], x_history[:,1], 'o')
#限定坐标显示范围
plt.xlim(-3.5, 3.5)
plt.ylim(-4.5, 4.5)
plt.xlabel("X1")
plt.ylabel("X2")
plt.show()
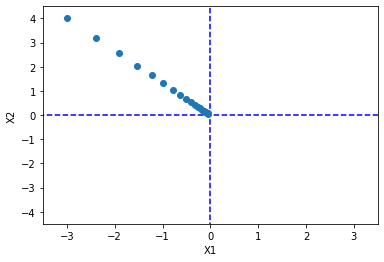
不错,效果拔群。从图像就可以看出来,当坐标离最小值越远,梯度也就越大,所以单次步长更新的数值也就越大;当逐渐靠近最小值的时候,梯度变小了,所以虽然步长不变,但单次更新的值也会变小。
那么学习率的值到底怎么确定呢?学习率的值在0到1之间,小了不行,大了也不行。就比如说我们走路,有步子迈的大的,也有小的。大的缺点就是容易一下子走过头了,而且容易卡住,然后怎么也迈不到那个最小的地方。学习率太小了,步子迈的太多,就很慢。所以当迭代次数不够的时候,你都还没走到目的地。
比如我修改学习率到0.05,看看结果: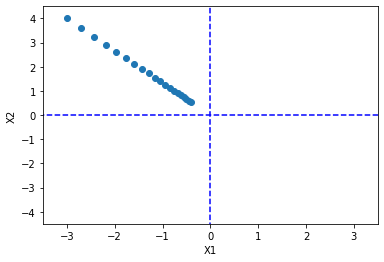
可以看到,这个还没到最小值就迭代完了,不过你可以把迭代次数弄多一点就好了。
再修改学习率到0.3: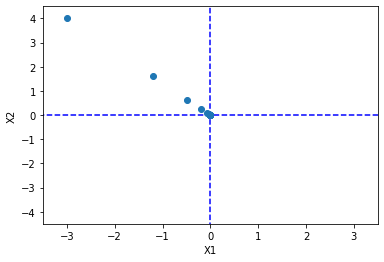
可以看到,前面步子迈的很大,一下子跨了那么多。而后面则是因为梯度值的变化,所以即使学习率依然很大,但是没有跨过头。但这里没有出现的情况不代表神经网络算法更新的时候不会出现跨过头的问题。这个后面再讲。
边栏推荐
- Use matlab to realize: chord cut method, dichotomy, CG method, find zero point and solve equation
- CONDA common commands
- [paper introduction] r-drop: regulated dropout for neural networks
- Point cloud data understanding (step 3 of pointnet Implementation)
- How do vision transformer work? [interpretation of the paper]
- PointNet原理证明与理解
- Handwritten call, apply, bind
- The difference and understanding between generative model and discriminant model
- 【MobileNet V3】《Searching for MobileNetV3》
- [tricks] whiteningbert: an easy unsupervised sentence embedding approach
猜你喜欢
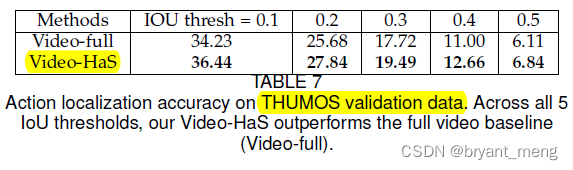
【Hide-and-Seek】《Hide-and-Seek: A Data Augmentation Technique for Weakly-Supervised Localization xxx》

What if a new window always pops up when opening a folder on a laptop

Faster-ILOD、maskrcnn_benchmark安装过程及遇到问题

Correction binoculaire
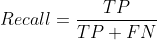
Common machine learning related evaluation indicators

【AutoAugment】《AutoAugment:Learning Augmentation Policies from Data》
图片数据爬取工具Image-Downloader的安装和使用

Sorting out dialectics of nature
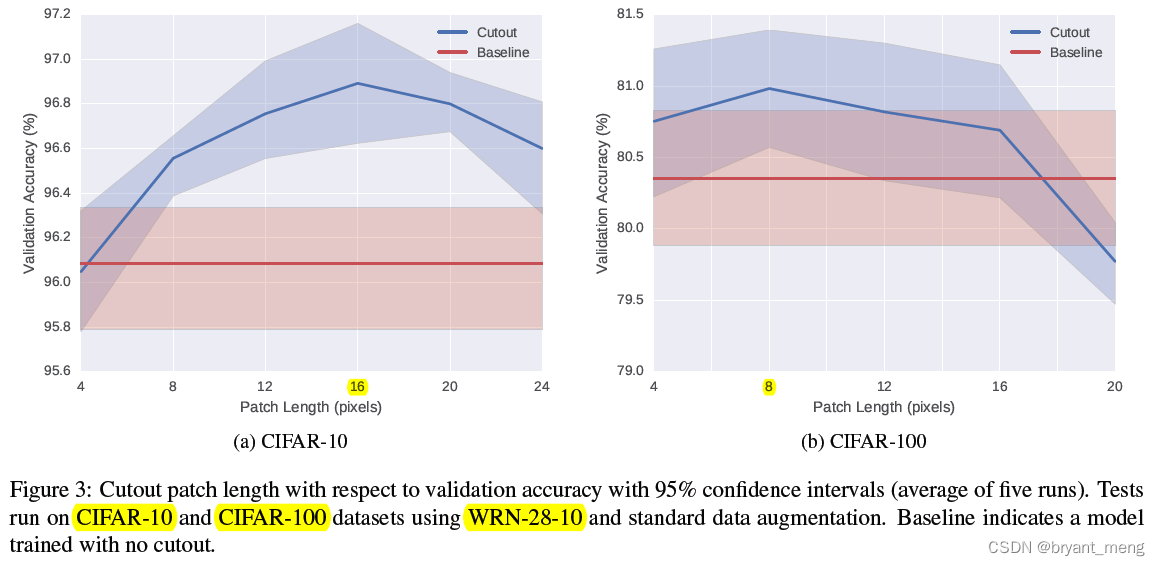
【Cutout】《Improved Regularization of Convolutional Neural Networks with Cutout》

【MagNet】《Progressive Semantic Segmentation》
随机推荐
Use matlab to realize: chord cut method, dichotomy, CG method, find zero point and solve equation
Sorting out dialectics of nature
传统目标检测笔记1__ Viola Jones
One book 1078: sum of fractional sequences
Determine whether the version number is continuous in PHP
ModuleNotFoundError: No module named ‘pytest‘
【AutoAugment】《AutoAugment:Learning Augmentation Policies from Data》
【Sparse-to-Dense】《Sparse-to-Dense:Depth Prediction from Sparse Depth Samples and a Single Image》
Calculate the total in the tree structure data in PHP
conda常用命令
Alpha Beta Pruning in Adversarial Search
论文写作tip2
深度学习分类优化实战
Play online games with mame32k
What if the laptop can't search the wireless network signal
Latex formula normal and italic
CONDA creates, replicates, and shares virtual environments
MMDetection模型微调
[CVPR‘22 Oral2] TAN: Temporal Alignment Networks for Long-term Video
TimeCLR: A self-supervised contrastive learning framework for univariate time series representation