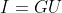第二十七章：时间复杂度与优化

2022-08-02 14:10:00 【WANGHAOXIN364】

阅读本文前，请确保已经学会C++的基本知识，包括：三大结构（顺序、分支、循环）、数组、字符串等相关知识。
部分题目可能要求掌握相应的基础算法。

一、小灰与大黄的故事

二、怎么衡量代码的好坏

让我们来想象一个场景：某一天，小灰和大黄同时加入了一个公司......

一天过后，小灰和大黄各自交付了代码，两端代码实现的功能都差不多。大黄的代码运行一次要花0.1秒，内存占用5MB。小灰的代码运行一次要花100秒，内存占用500MB。于是......

由此可见， 衡量代码的好坏，包括两个非常重要的指标 ：

1.运行时间；

2.占用空间。

三、基本操作执行次数

关于代码的运行时间，我们一般用程序的基本操作执行次数来计算，我们用四个生活中的场景，来做一下比喻：

场景1：

给小灰一条长10寸的面包，小灰每3天吃掉1寸，那么吃掉整个面包需要几天？

答案自然是 3 × 10 = 303×10=30 天。

如果面包的长度是 NN 寸呢？

此时吃掉整个面包，需要 3 × n = 3n3×n=3n 天。

如果用一个 数学函数 来表达这个相对时间，可以记作 T(n)=3nT(n)=3n 。

我们如果用C++程序来实现这个问题，那么代码如下：

int main()
{
    int n;
    cin >> n;
    for(int i = 0; i < n; i++)
    {
        cout << "第一天，等待" << endl;
        cout << "第二天，等待" << endl;
        cout << "第三天，吃掉一寸面包" << endl;
    }
}

Copy

场景2：

给小灰一条长16寸的面包，小灰每5天吃掉面包剩余长度的一半，第一次吃掉8寸，第二次吃掉4寸，第三次吃掉2寸......那么小灰把面包吃得只剩下1寸，需要多少天呢？

这个问题翻译一下，就是数字16不断地除以2，除几次以后的结果等于1？这里要涉及到数学当中的对数，以2为底，16的对数，可以简写为 log_216log216 ，这个式子算的结果就是4了。我们在计算机中一般简记为 log16log16 。

因此，把面包吃得只剩下1寸，需要 5 × log16 = 5 × 4 = 205×log16=5×4=20 天。

如果面包的长度是 NN 寸呢？

需要 5 × logn = 5logn5×logn=5logn 天，记作 T(n)= 5lognT(n)=5logn 。

代码如下：

int main()
{
    int n;
    cin >> n;
    for(int i = 1; i < n; i = i * 2)
    {
        cout << "第一天，等待" << endl;
        cout << "第二天，等待" << endl;
        cout << "第三天，等待" << endl;
        cout << "第四天，等待" << endl;
        cout << "第五天，吃掉一寸面包" << endl;
    }
}

Copy

场景3：

给小灰一条长10寸的面包和一个鸡腿，小灰每2天吃掉一个鸡腿。那么小灰吃掉整个鸡腿需要多少天呢？

答案自然是2天。因为只说是吃掉鸡腿，和10寸的面包没有关系。

如果面包的长度是 NN 寸呢？

无论面包有多长，吃掉鸡腿的时间仍然是2天，记作T(n)= 2T(n)=2 。

int main()
{
    int n;
    cin >> n;
    cout << "第一天，等待" << endl;
    cout << "第二天，吃掉一个鸡腿" << endl;
}

Copy

场景4：

给小灰一条长10寸的面包，小灰吃掉第一个一寸需要1天时间，吃掉第二个一寸需要2天时间，吃掉第三个一寸需要3天时间.....每多吃一寸，所花的时间也多一天。那么小灰吃掉整个面包需要多少天呢？

答案是从1累加到10的总和，也就是55天。

如果面包的长度是 NN 寸呢？

此时吃掉整个面包，需要 1+2+3+......+ n-1 + n = \frac{(1+n)*n}{2} = 0.5n^2 + 0.5n1+2+3+......+n−1+n=2(1+n)∗n=0.5n2+0.5n。记作 T(n) = 0.5n^2 + 0.5nT(n)=0.5n2+0.5n。

程序如下：

int main()
{
    int n;
    cin >> n;
    for(int i = 0; i < n; i++)
    {
        for(int j = 0; j <= i; j++)
        {
            cout << "等待一天" << endl;
        }
        cout << "吃一寸面包" << endl;
    }
}

Copy

上面所讲的是吃东西所花费的相对时间，这一思想同样适用于对程序基本操作执行次数的统计。

四、时间复杂度

有了基本操作执行次数的函数 T(n)T(n)，是否就可以分析和比较一段代码的运行时间了呢？还是有一定的困难。

比如算法A的相对时间是T(n) = 100nT(n)=100n，算法B的相对时间是T(n) = 5n^2T(n)=5n2，这两个到底谁的运行时间更长一些？这就要看n的取值了。

所以，这时候有了 渐进时间复杂度 (asymptotic time complexity)的概念，官方的定义如下：

若存在函数 f(n)f(n)，使得当n趋近于无穷大时，\frac{T(n)}{f(n)}f(n)T(n)的极限值为不等于零的常数，则称 f(n)f(n)是 T(n)T(n)的同数量级函数。

记作 T(n)= O(f(n))T(n)=O(f(n))，称O(f(n))O(f(n)) 为算法的渐进时间复杂度， 简称时间复杂度 。

渐进时间复杂度用大写字母O来表示，所以也被称为大O表示法。

如何推导出时间复杂度呢？有如下几个原则：

如果运行时间是常数量级，用常数1表示；
只保留时间函数中的最高阶项；
如果最高阶项存在，则省去最高阶项前面的系数。

让我们回头看看刚才的四个场景。

场景1：

T(n) = 3nT(n)=3n

最高阶项为3n，省去系数3，转化的时间复杂度为：

T(n)= O(n)T(n)=O(n)

场景2：

T(n) = 5lognT(n)=5logn

最高阶项为5logn5logn，省去系数5，转化的时间复杂度为：

T(n) = O(logn)T(n)=O(logn)

场景3：

T(n) = 2T(n)=2

只有常数量级，转化的时间复杂度为：

T(n) = O(1)T(n)=O(1)

场景4：

T(n) = 0.5n^2 + 0.5nT(n)=0.5n2+0.5n

最高阶项为0.5n^20.5n2，省去系数0.50.5，转化的时间复杂度为：

T(n) = O(n^2)T(n)=O(n2)

这四种时间复杂度究竟谁用时更长，谁节省时间呢？稍微思考一下就可以得出结论：

O(1)< O(logn)< O(n)< O(n^2)O(1)<O(logn)<O(n)<O(n2)

在编程的世界中有着各种各样的算法，除了上述的四个场景，还有许多不同形式的时间复杂度，比如：

O(nlogn), O(n^3), O(m*n)，O(2^n)，O(n!)O(nlogn),O(n3),O(m∗n)，O(2n)，O(n!)

今后遨游在代码的海洋里，我们会陆续遇到上述时间复杂度的算法。

时间复杂度的巨大差异

我们举一个栗子：

现在我们有个任务让非常厉害的两位神犇来完成，预测合肥市近 nn 天的天气。现在两位神犇各自设计了一个算法程序。

算法A的相对时间规模是T(n)= 100nT(n)=100n，时间复杂度是O(n)O(n)

算法B的相对时间规模是T(n)= 5n^2T(n)=5n2，时间复杂度是O(n^2)O(n2)

算法A运行在小灰家里的老旧电脑上；算法B运行在某台超级计算机上，运行速度是老旧电脑的100倍。

那么，随着输入规模 n 的增长，两种算法谁运行更快呢？

640?wx_fmt=png

从表格中可以看出，当n的值很小的时候，算法A的运行用时要远大于算法B；当n的值达到1000左右，算法A和算法B的运行时间已经接近；当n的值越来越大，达到十万、百万时，算法A的优势开始显现，算法B哪怕用了非常牛的计算机，依然会越来越慢，差距越来越明显。

这就是不同时间复杂度带来的差距。

五、时间复杂度的优化

一般而言，在我们的竞赛中，程序会限制1秒的时间，那这个1秒是什么概念呢？我们可以把1秒描述为 程序执行了大约3亿次的基本操作执行次数的时间 。

int n, s=0;//运行1次
n = 100000000;//运行1次
for(int i = 0; i < n; i++)//运行1亿次
{
    s++;//运行1亿次
}
cout<<s;//运行1次

Copy

我们把基本操作次数加在一起，这个程序运行了200000003次。也就是说上面这个程序没有超过时间。
【注1】部分省市的机器性能可能好一些，3亿次 ~ 4亿次可能也不会超时。但是5亿次以上，考试的机器基本都会超时了。
【注2】一般我们可以把上面的程序视为2亿次的操作次数。相较于2亿次，后面多的3次、或是万次、还是百万次基本上可以忽略不计。

但是那么下面这个程序呢？

int n, s=0;//运行1次
n = 20000;//运行1次
for(int i = 0; i < n; i++)//运行20000次
{
    for(int j = 0; j < n; j++)//运行20000×20000次
    {
        s++;//运行20000×20000次
    }
}
cout<<s;//运行1次

Copy

因为该程序是双重循环，内层循环执行的次数就是20000×20000次，总计1+1+20000+20000×20000+20000×20000+1 = 800020003 ≈ 8亿次，超过了竞赛中的要求，就会 出现超时 的情况。

无论是竞赛，还是日常学习过程中，我们都希望一个程序的运行时间越短越好。为什么我们需要性能很好的程序呢？

还是之前举的例子：我们要计算合肥市近7天的天气。考虑的因素非常多，比如：温度、湿度、压强、风向、风速、地理环境、生态环境等等这些因素。

此时，你写了一个程序，需要运行10天才能算出来，那等你算出来，黄瓜菜都凉了，还用预测吗？

我们可以使用时间更短、更优化的算法在1个小时内就算出来，这才是非常有用的程序！

下面我们看几个例题，来感受一下效率优化带来的速度提升。

7.例题

第一种方式，每个服务员都会找 nn 次，总共 nn 个服务员，所以总计执行 n^2n2 次。所以时间复杂度为O(n^2)O(n2)；
第二种方式，第一个服务员找 nn 次，第二个服务员找 \frac{n}{2}2n 次，第三个服务员找 \frac{n}{3}3n 次，......，一直到最后一个服务员只要找到 11 次，所以总计 (1+\frac{1}{2}+\frac{1}{3}+...+\frac{1}{n})×n(1+21+31+...+n1)×n 次，而前面这个1+\frac{1}{2}+\frac{1}{3}+...+\frac{1}{n}1+21+31+...+n1 相当于 lognlogn，所以时间复杂度为 O(nlogn)O(nlogn) ；

程序的使用时间 （用时） 可以近似的用下面的式子简单计算：

用时秒数 \approx \frac{执行次数}{3亿}用时秒数≈3亿执行次数

我们可以分析这两种方式的时间复杂度和用时：

数据范围	方法一，时间复杂度为 O(n^2)O(n2)	方法二，时间复杂度为 O(nlogn)O(nlogn)
n=10000n=10000	执行次数为1亿，约为0.3s	执行次数约为9万，约为1ms
n=20000n=20000	执行次数为4亿，约为1.3s	执行次数约为20万，约为2ms
n=50000n=50000	执行次数为25亿，约为8s	执行次数约为25万，约为2ms
n=100000n=100000	执行次数为100亿，约为33s	执行次数约为115万，约为10ms

所以我们提交两个代码之后，可以对比两个程序每一个测试点的用时，发现方法一对于后面50%的测试点，是会超时的,，而且第4、5两个测试点用时几百毫秒，也挺大的了；但是第二个程序，所有测试点的用时都很短，基本每个点用时都在10ms以内。

T2：来，骗

需要掌握知识点：一维数组、前缀和。

直接暴力走一遍，可以通过60%的测试点。可以手动算一下下面暴力程序的用时。

#include<bits/stdc++.h>
using namespace std;
int main()
{
    int n,a[1000010],q,l,r,sum;
    cin>>n;
    for(int i=1;i<=n;i++)
        cin>>a[i];
    cin>>q;
    for(int i=1;i<=q;i++)
    {
        cin>>l>>r;
        sum=0;
        for(int j=l;j<=r;j++)
        {
            sum+=a[j];
        }
        cout<<sum<<endl;
    }
}

Copy

使用前缀和优化。

#include<bits/stdc++.h>
using namespace std;
const int N = 1e6+5;
int q, n, a[N], s[N], l, r;
int main()
{
    cin >> n;
    for(int i = 1; i <= n; i++)
    {
        cin >> a[i];
        s[i] = s[i-1]+a[i];   // 计算前缀和
    }
    cin >> q;
    for(int i = 1; i <= q; i++)  // q 次查询
    {
        cin >> l >> r;
        cout << s[r]-s[l-1] << endl;
    }
    return 0;
}

Copy

T3：素数距离

需要掌握知识点：一维数组、素数、素数筛。

本题考察素数的判断，对于素数的判断问题，如果需要对大量数字去判断是否是素数，就最好采用素数筛的方法，这样可以有效避免超时。本题数据范围较大，最多需要判断 800 万个数字是否是素数，因此，采用素数筛。

当确定了所有的素数之后，我们还需要去判断素数之间的距离，但是要求相邻，因此，我们可以在找到素数之后，按数字大小，将所有的素数存进数组里，如此，我们只需再遍历数组，计算相邻元素之间的差值，就可以很轻易地去找到最近或最远的相邻素数。

参考代码如下：

#include<bits/stdc++.h>
using namespace std;
int l, r, mx, mn = 1e9;
bool s[8000010]={1,1,0};   // 素数筛数组
int p[8000010], cnt, a , b, c, d;

// 埃氏筛标记素数，并将 [l, r] 内的素数保存进 p 数组
void prime(int l, int r){
    s[0]=s[1]=1;
    for(int i = 2; i <= r; i++){
        if(!s[i]){
            if(i >= l){   // 素数在 l~r 之间
                p[++cnt] = i;
            }
            for(int j = 2*i; j <= r; j += i){
                s[j] = 1;
            }
        }
    }
}
int main()
{
    cin >> l >> r;
    prime(l, r);  // 查找素数，并放入 p 中
    if(cnt < 2) {
        cout<<"There are no adjacent primes.";
        return 0;
    }
    // 遍历所有素数，找出最大和最小相邻素数对
    for(int i = 2; i <= cnt; i++) {
        if(p[i]-p[i-1] > mx){
            mx = p[i]-p[i-1];  
            a = p[i-1];
            b = p[i];
        }
        if(p[i] - p[i-1] < mn){
            mn = p[i] - p[i-1];
            c = p[i-1];
            d = p[i];
        }
    }
    printf("%d,%d are closest, %d,%d are most distant.",c,d,a,b);
    return 0;
}

Copy

例题不是很多，主要是各种不同的题目要用不同的算法优化时间，需要多思考解题思路。