Merge sort

The content and code of this article come from the data structure textbook .
Merge sort (Merging Sort) Is another kind of different sorting method ." Merger " The meaning of will is 2 Or 2 More than ordered tables are combined into 1 New ordered table . Whether it is sequential storage or linked list storage structure , All available O(m+n) In terms of time . The basic idea of merging is as follows ：
Suppose the initial sequence contains n A record , We can view it as n Two ordered subsequences , The length of each subsequence is 1, And then they merge , obtain $\lceil \frac{n}{2}\rceil$ A length of 2 or 1 An ordered subsequence of ; And then we merge ,… …, repeat , All the way to a length of zero n The ordered sequence of , This sorting method is called 2- Path merging and sorting . Here's the picture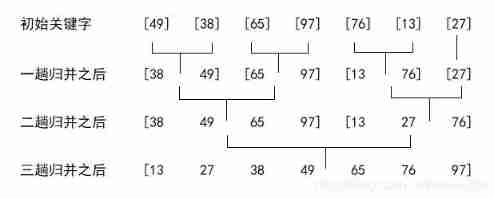

2- The core operation in path merging sorting is to merge two adjacent ordered sequences in a one-dimensional array into an ordered sequence .
java Realization

	void merge(int[] sr, int[] tr, int i, int m, int n) {
    
		if (i == n) {
    	//  Processing of the last element of the array 
			tr[i] = sr[i];
			return;
		}
		int k = 0;
		int j = 0;
		//  take SR[i..m] and SR[m+1..n] Merge into ordered TR[i..n]
		for (j = m + 1, k = i; i <= m && j <= n; ++k) {
    
			if (sr[i] <= sr[j])		//  take SR From small to large TR
				tr[k] = sr[i++];
			else
				tr[k] = sr[j++];
		}

		if (i <= m) {
    
			for (int u = i, q = 0; u <= m; u++) {
    //  Put the rest SR[i...m] Copied to the TR
				tr[k + q] = sr[u];
				++q;
			}

		}

		if (j <= n) {
    
			for (int u = j, q = 0; u <= n; u++) {
    //  Put the rest SR[j...n] Copied to the TR
				tr[k + q] = sr[u];
				++q;
			}

		}

	}
	
	int[] mergSort(int[] arr) {
    
		int[] sr = arr;
		int[] tr = new int[arr.length];

		int h = 1, len = arr.length;
		//  It takes several times to merge , With 2 Bottom ,len The logarithm of is rounded up .
		int count = (int) Math.ceil(log(len, 2));

		for (int x = 0; x < count; x++) {
    
			//  In each trip , The number of groups that need to be merged ,len/2h The decimal obtained is rounded up .
			int ceil = (int) Math.ceil((float) len / (2 * h));
			for (int y = 0; y < ceil; y++) {
    
				int i = y * 2 * h;
				int m = i + h - 1;
				int n = m + h;
				n = n >= len ? n - 1 : n;//  Subscript processing of the last element of the array 
				merge(sr, tr, i, m, n);
			}

			//  Save the result of one sort to the original array 
			for (int z = 0; z < tr.length; z++) {
    
				arr[z] = tr[z];
			}

			//  Subsequence length modification 
			h *= 2;
		}

		return tr;
	}
	
	/** *  Logarithmic method , This method uses the bottom changing formula in logarithm in mathematics to realize . *  because JDK There is no request 2 Method of logarithm of base . * @param value * @param base * @return */
	double log(double value, double base) {
    
		return Math.log(value) / Math.log(base);
	}
	
	@Test
	public void fun1(){
    
		int[] arr = new int[] {
     49, 38, 65, 97, 76, 13, 27 };
		int[] tr = mergSort(arr);
		System.out.println(Arrays.toString(tr));		
	}

The operation of merging and sorting is , call $\lceil \frac{n}{2h}\rceil$(n/2h The decimal result after is rounded up , Such as 2.01 Rounded up to 3) Sub algorithm merge take SR[1…n] The middle is adjacent to the front and back and the length is $h$ The ordered segments of are merged in pairs , Get adjacent before and after 、 The length is $2h$ Ordered segment of , And stored in TR[1…n] in , The whole merging and sorting needs to be done $\lceil {\log }_{2}n\rceil$ Trip to . so , The realization of merging and sorting requires a number of auxiliary spaces such as records to be arranged , So it's Spatial complexity by O(n), Its Time complexity by O(nlogn).

And Quick sort and Heap sort comparison , The biggest feature of merging and sorting is , It is a stable sorting method . Looks like Java JDK in Collections.sort(List); The method is to merge and sort or an improved version .

this 2 Mathematical library functions for calculating logarithms and rounding up are used in both language versions , By Math Classes and math.h The header file provides .
When calculating logarithms, there is an implementation method of using the bottom exchange formula of logarithms , The original mathematical formula is as follows ：
about $a,c\in (0,1)\cup (1,+\infty )$ And $b\in (0,+\infty )$, Yes
${\log }_{a}b=\frac{{\log }_{c}b}{{\log }_{c}a}$

Here is C/C++ Implementation version of .

/* *  Merge sort  *  data structure (C Language version )  YanWeiMin   Wei-min wu  * */
#include<iostream>
#include<math.h>

using namespace std;

/** *  Logarithmic method  * @param value * @param base * @return */
double logPlus(double value, double base) {
    
	return log(value) / log(base);
}

void merge(int sr[], int tr[], int i, int m, int n) {
    
	if (i == n) {
    //  Processing of the last element of the array 
		tr[i] = sr[i];
		return;
	}
	int k = 0;
	int j = 0;
	// System.out.println(i+","+m+","+n);
	for (j = m + 1, k = i; i <= m && j <= n; ++k) {
    
		if (sr[i] <= sr[j]) {
    
			tr[k] = sr[i++];
		} else {
    
			tr[k] = sr[j++];
		}
	}

	if (i <= m) {
    
		//  Put the rest SR[i...m] Copied to the TR
		for (int u = i, q = 0; u <= m; u++) {
    
			tr[k + q] = sr[u];
			++q;
		}

	}

	if (j <= n) {
    
		//  Put the rest SR[j...n] Copied to the TR
		for (int u = j, q = 0; u <= n; u++) {
    
			tr[k + q] = sr[u];
			++q;
		}

	}

}

int* mergSort(int arr[], int arrLength) {
    
	int* sr = arr;
	int* tr = new int[arrLength];//  Allocate memory for array pointers , Otherwise, a segment error will be reported, and the core has been dumped 

	int h = 1, len = arrLength;
	//  It takes several times to merge , With 2 Bottom ,len The logarithm of is rounded up .
	int count = (int) ceil(logPlus(len, 2));

	for (int x = 0; x < count; x++) {
    
		//  In each trip , The number of groups that need to be merged ,len/2h The decimal obtained is rounded up .
		int _ceil = (int) ceil((float) len / (2 * h));
		for (int y = 0; y < _ceil; y++) {
    
			int i = y * 2 * h;
			int m = i + h - 1;
			int n = m + h;
			n = n >= len ? n - 1 : n;//  Subscript processing of the last element of the array 
			merge(sr, tr, i, m, n);
		}

		//  Save the result of one sort to the original array 
		for (int z = 0; z < arrLength; z++) {
    
			arr[z] = tr[z];
		}

		//  Subsequence length modification 
		h *= 2;
	}

	return tr;
}


int main(int argc, char* argv[]) {
    
	int arr[] = {
     49, 38, 65, 97, 76, 13, 27 };
	int* tr = mergSort(arr, 7);

	for(int i=0;i<7;i++){
    
		cout<<tr[i]<<" ";
	}
	cout<<endl;
	return 0;
}

Finally, there is a version of recursive implementation
The original pseudo code is as follows ：

void MSort(RcdType SR[], RcdType &TR1[], int s, int t){
    
	//  take SR[s..t] The order of merging is TR1[s..t].
	if(s == t) TR1[s]=SR[s];
	else{
    
		m = (s+t)/2;
		MSort(SR, TR2,s,m);
		MSort(SR, TR2,m+1,t);
		Merge(TR2, TR1, s, m, t);
	}
}// MSort

void MergeSort(SqList &L){
    
	//  For the sequence table L Merge and sort 
	MSortt(L.r, L.r, 1, L.length);
}//MergeSort

The above pseudocode has never been converted successfully , So I rewritten a version . This pseudo code means to split the array until there is 1 Individual elements , Then continue to merge in pairs , Keep going forward and backward , Until the final array is ordered . This recursive process is like the preorder traversal of a binary tree , Finally, return to , Form an ordered array , However, it this TR1,TR2 I really don't know what to say .
Rewrite as follows ：

	void mergeV2(int[] sr, int[] tr, int i, int m, int n) {
    
		int k = 0;
		int j = 0;
		//  take SR[i..m] and SR[m+1..n] Merge into ordered TR[i..n]
		for (j = m + 1, k = i; i <= m && j <= n; ++k) {
    
			if (sr[i] <= sr[j]) //  take SR From small to large TR
				tr[k] = sr[i++];
			else
				tr[k] = sr[j++];
		}

		if (i <= m) {
    
			for (int u = i, q = 0; u <= m; u++) {
    //  Put the rest SR[i...m] Copied to the TR
				tr[k + q] = sr[u];
				++q;
			}

		}

		if (j <= n) {
    
			for (int u = j, q = 0; u <= n; u++) {
    //  Put the rest SR[j...n] Copied to the TR
				tr[k + q] = sr[u];
				++q;
			}

		}

	}
	
	// Recursive implementation , complete . It is slightly different from pseudo code 
	void MSortV2(int[] sr, int[] tr1, int s, int t) {
    
		if (s == t) {
    
			tr1[s] = sr[t];
		} else {
    
			int m = (s + t) / 2;
			MSortV2(sr, tr1, s, m);
			MSortV2(sr, tr1, m + 1, t);
			mergeV2(sr, tr1, s, m, t);
			for (int i = s; i <= t; i++) {
    
				sr[i] = tr1[i];
			}
		}
	}
	
	@Test
	public void fun3() {
    
		int[] arr = new int[] {
     49, 38, 65, 97, 76, 13, 27 };
		int[] tr1 = new int[7];
		MSortV2(arr, tr1, 0, arr.length - 1);
		System.out.println(Arrays.toString(tr1));

	}