Knapsack problem and 0-1 knapsack problem

knapsack problem

Yes n Two items and a backpack , Design items i The value of vi , Weight is wi , You can choose a part of each item to put into the backpack , Asking how to put items can maximize the total value of the backpack .
Solve with greed

0-1 knapsack problem

Yes n Two items and a backpack , The capacity of the backpack is c, goods i The weight of is wi, The value is vi, There are only two choices for each item: put it in the backpack or not , Ask which items can maximize the total value if the backpack capacity allows .

* Greedy method to solve the knapsack problem

* Dynamic programming solves 0-1 knapsack problem

Ideas ：
① Dynamic programming solves 0-1 The basic idea of knapsack problem is , Consider one thing by one , This is from n Start thinking （ From the first one can also , Essentially the same , It's just that the subscript of some data is different from the meaning of the representation , The procedure is also different , One is easy to understand the other , Here from the n Start thinking about it as an example ）, Each time, consider whether the current item can be put , Whether the value brought by putting it is worth

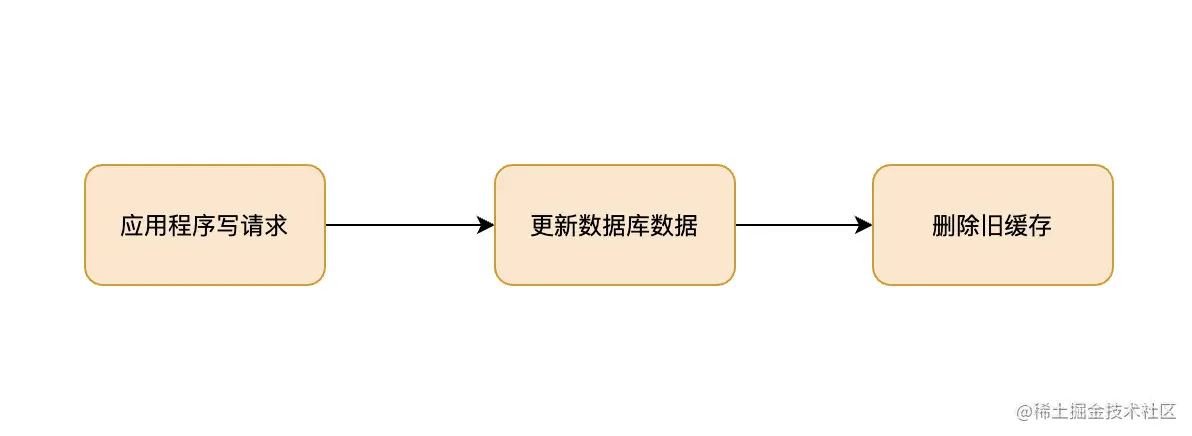
② set up m(i,j) The capacity of the backpack is j, The optional items are i~n The optimal value of , Put items into Backpack Capacity j Will change .
for example m(1,c) Express , All items are optional , The current capacity of the backpack is c The optimal value of , That is the solution of the problem . First consider the second n Items to choose from , Find out m[n,c], Consider the next item one by one , Until we find the solution

③ Then there is the following recursion , This is the core of understanding this problem , Make these recursive formulas clear and solve them by dynamic programming 0-1 The knapsack problem is basically mastered （w It's the weight ,v It's value ）

Consider only the n Items ：
m(n,j)=0 j< Wn ( There is no place to pack things on the back n)
m(n,j)=Vn j>= Wn ( Backpacks can hold items n)

If the item i I can't put it in , consider i~n Actually, it's about thinking about i+1 To n：
m(i,j)= m(i+1,j) j<Wi ( There is no place to pack things on the back i）

If you can put it in , Then consider having items i And nothing i Which is of great value
m(i,j)=max{m(i+1,j) , m(i+1,j-Wi) +Vi} j>=Wi

The procedure is as follows ：

The following procedure determines which items are put into the backpack

* Backtracking solution 0-1 knapsack problem

Use backtracking to solve 0-1 knapsack problem , To construct a subset tree

It is also a matter of consideration , One layer represents an object , The left subtree represents the current item , The right subtree represents not to put , Obviously, all items were considered when the tree searched the leaf node . If the backpack has enough capacity , Then enter the left tree , Otherwise don't go in , Enter when the right subtree may contain the optimal solution , When we don't have to enter the right subtree, we prune the right subtree , Under what circumstances is pruning ？

for example ：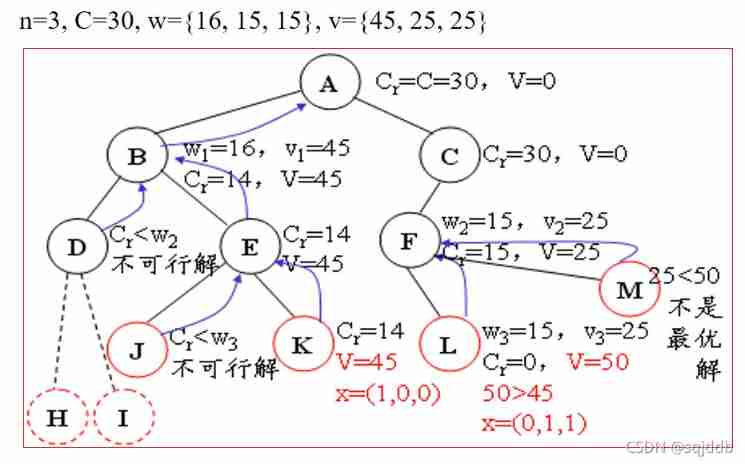

The procedure is as follows ：

* Branch and bound method to solve 0-1 knapsack problem

The basic idea ：
There are two ways ：

>> Queued

>> Priority queue