Implementation of AVL tree

Binary search tree

Introducing AVL Before the tree , Everyone should know binary search tree , actually AVL The tree is improved on the basis of binary search tree .

This picture is a binary search tree , It's not hard to see , If the nodes of the left subtree are smaller than the root node , The nodes of the right subtree are larger than the root node , This is very efficient for query operations .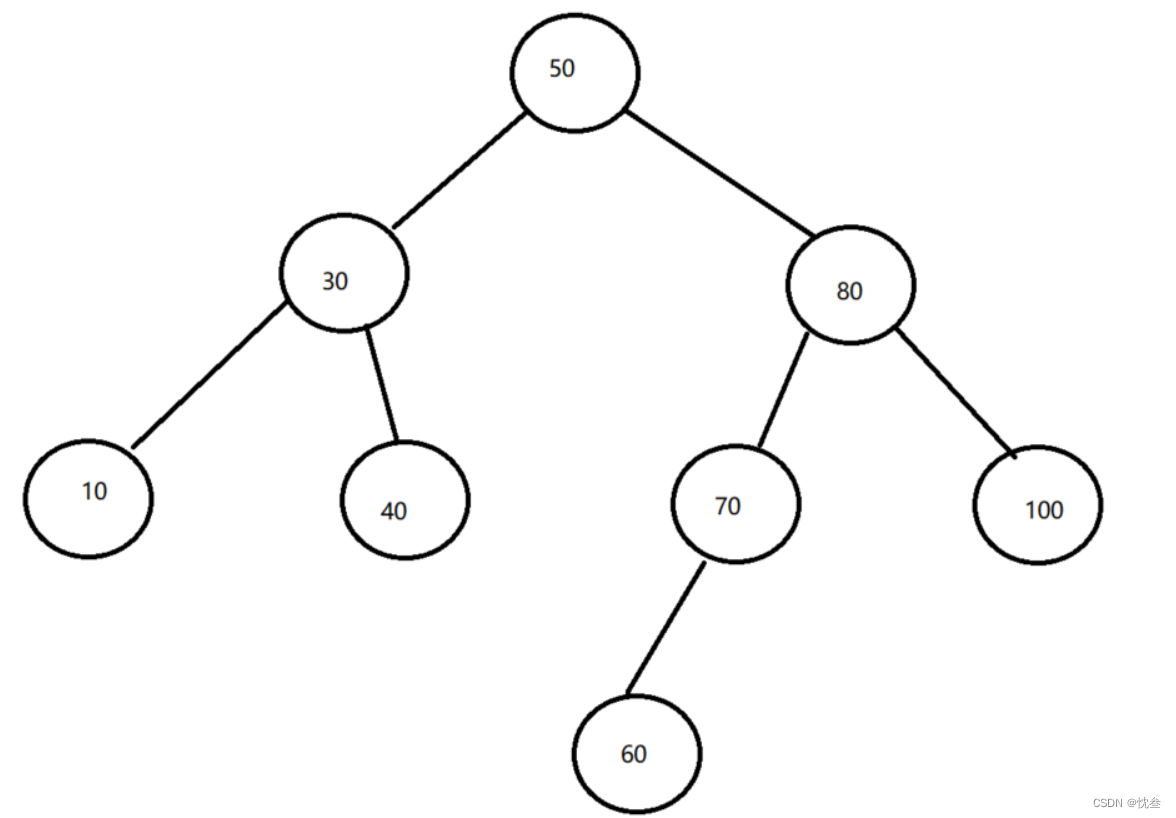

Binary search tree is also called binary sort tree , It could be an empty tree , Or a binary tree with the following properties :

• If its left subtree is not empty , Then the values of all nodes on the left subtree are smaller than the values of the root nodes
• If its right subtree is not empty , Then the value of all nodes on the right subtree is greater than the value of the root node
• Its left and right subtrees are also binary search trees

Use middle order traversal to traverse the tree , Is an ordered sequence ( Left root right )

Analyze the time complexity of binary search tree
When using binary search tree to search

The time complexity is O(logN), But this is the best case
Yes, yes. n A binary search tree of nodes , If the probability of finding each element is equal , Then the average search length of the binary search tree is a function of the depth of the node in the binary search tree , That is, the deeper the node , The more times you compare .
If the binary tree is a normal tree, the time complexity does not change , But if it is a single branch tree , Not so

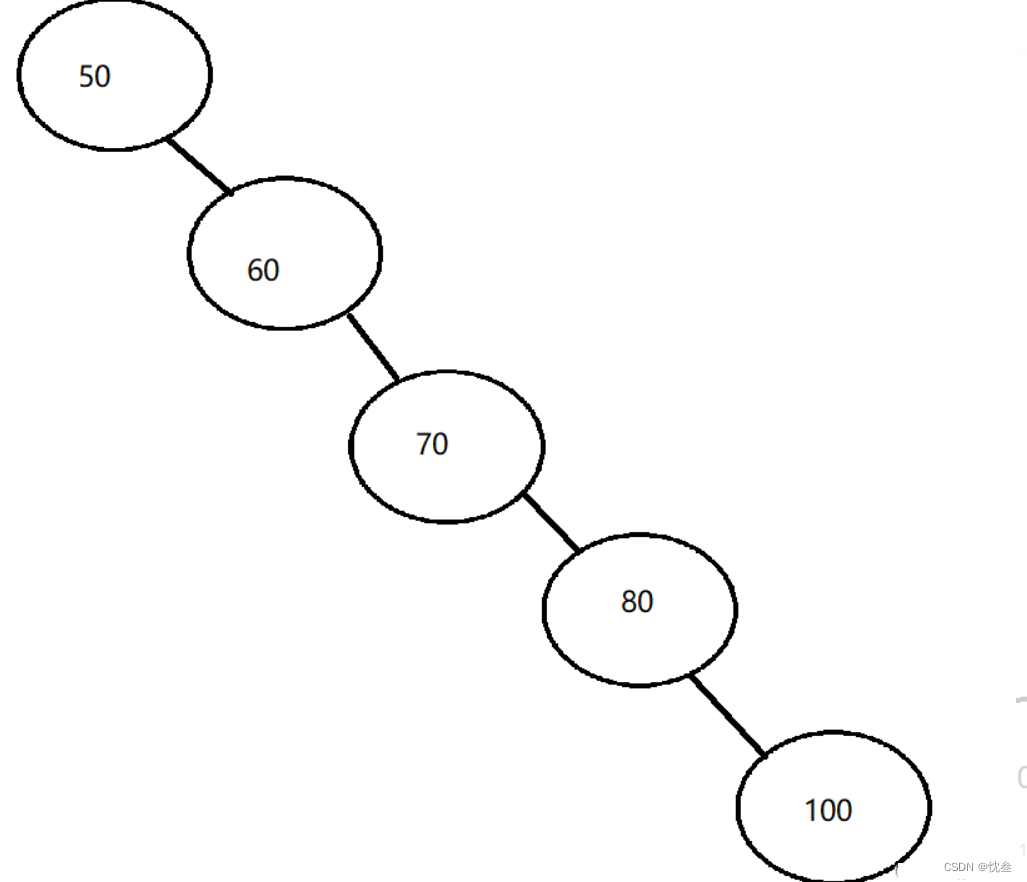
The average number of comparisons is : N/2
The average number of comparisons in the optimal case is log2N
Therefore, the improvement of binary search tree is to avoid the new inserted node becoming a single branch or a tree similar to a single branch ,
To what extent is it not similar to a single branch tree , Is to make a limit

Limit : When a new node is inserted into the binary search tree , If we can ensure that the absolute value of the height difference between the left and right subtrees of each node does not exceed 1( You need to adjust the nodes in the tree ), You can reduce the height of the tree , This reduces the average search length .

AVL Tree concept

Although binary search tree can shorten the search efficiency , However, if the data is ordered or close to ordered, the binary search tree will degenerate into a single branch tree , Finding elements is equivalent to searching for elements in the sequence table , inefficiency
therefore , Two Russian mathematicians G.M.Adelson-Velskii and E.M.Landis stay 1962 year A method for solving the above problems is invented ：
When a new node is inserted into the binary search tree , If we can ensure that the absolute value of the height difference between the left and right subtrees of each node does not exceed 1( You need to adjust the nodes in the tree ), You can reduce the height of the tree , This reduces the average search length .

A tree AVL Trees or empty trees , Or a binary search tree with the following properties ：

• Its left and right subtrees are AVL Trees
• The difference between the height of the left and right subtrees ( It's called equilibrium factor ) The absolute value of is not more than 1(-1/0/1)
  Here we assume
  Balance factor = Height of right subtree - Height of left subtree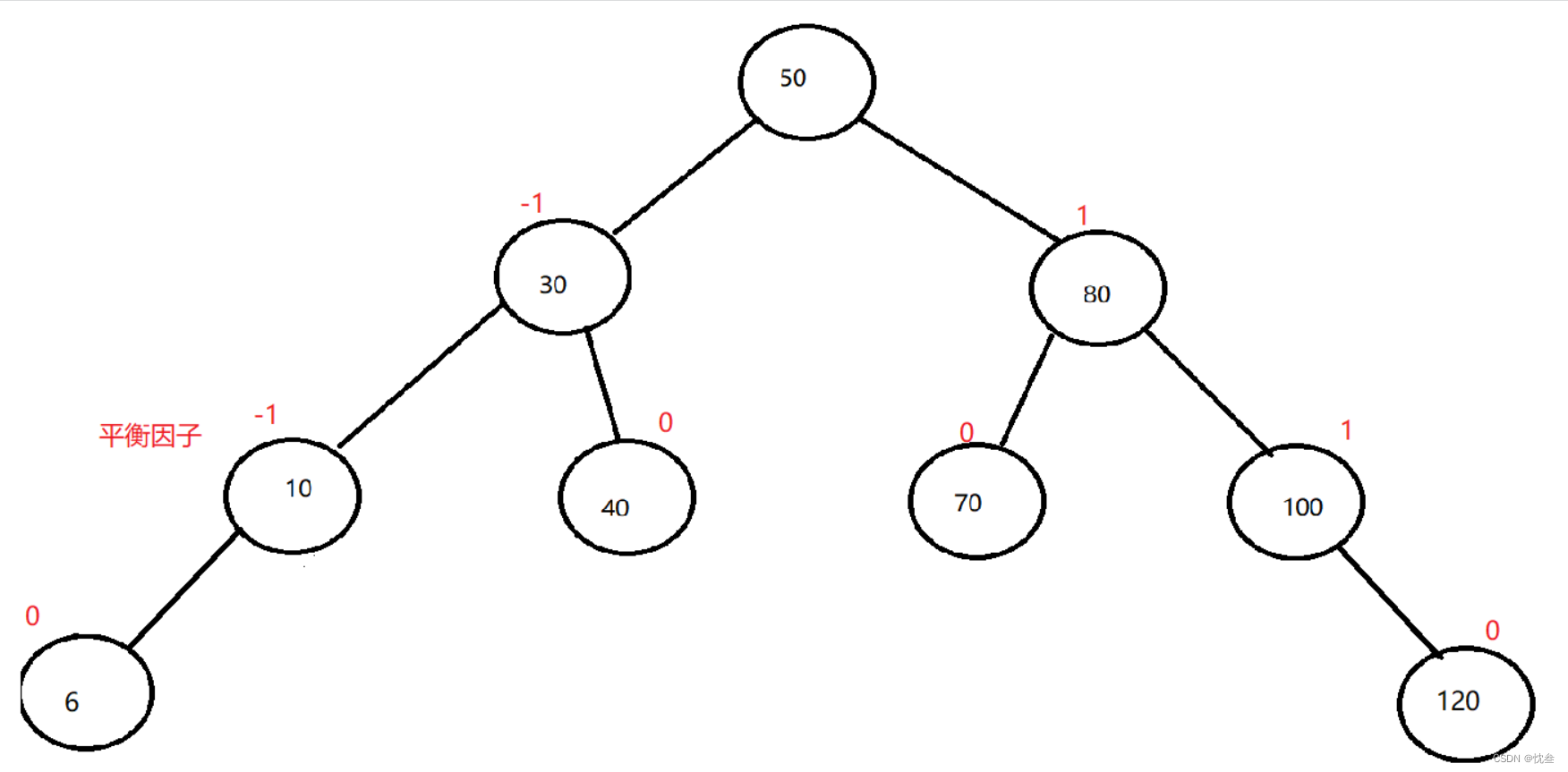
  
  Each node has a balance factor , Once the value of the balance factor of a node exceeds the range, it is not AVL Trees , It should be adjusted at this time , Just like big and small piles , In the process of inserting, ensure that the size of the heap , You need to adjust downward .

AVL Insertion of trees

actually AVL The insertion of trees is troublesome , Insert on the basis of binary search tree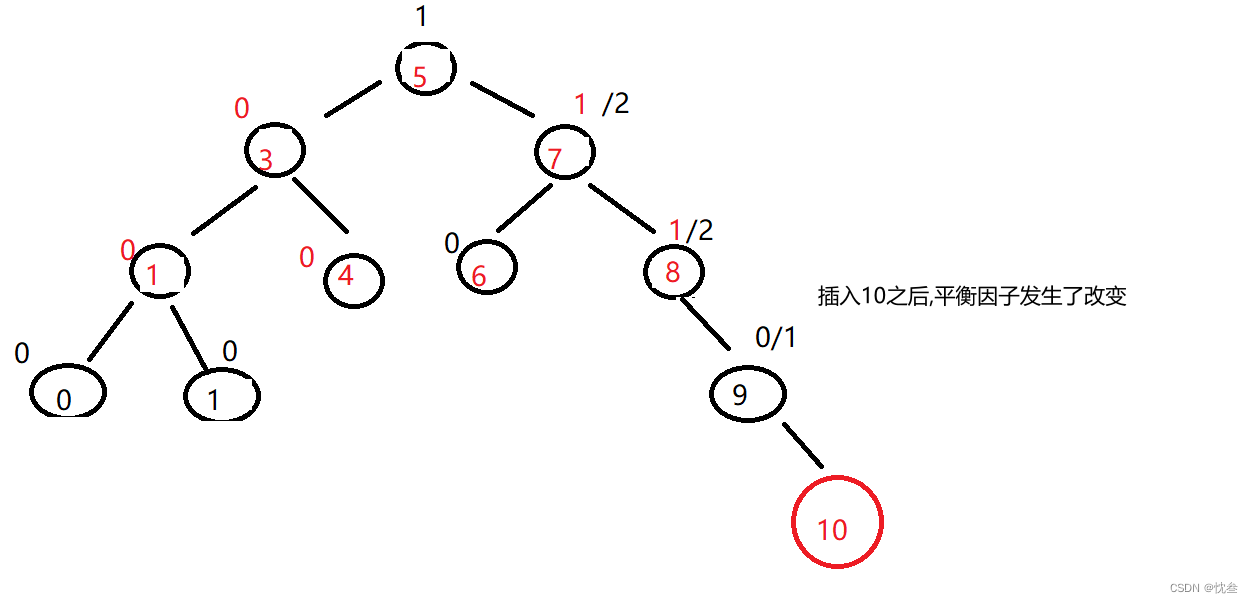

Let's analyze first , Suppose the inserted node val yes 10 This is the time , Equivalent to inserting into AVL The rightmost side of the tree , here 9 The equilibrium factor of ++,8 The equilibrium factor of ++, But in order to 8 The binary tree with the root node is not highly balanced , So we need to do rotate !!!

First, construct a AVL Trees

public class AVLTree {
    
    static class TreeNode {
    
        public int val;
        public int bf; //  Balance factor 
        public TreeNode left;
        public TreeNode right;
        public TreeNode parent;
        public TreeNode(int val) {
    
            this.val  = val;
        }
    }
    public TreeNode root;//  The root node 

The specific code inserted is implemented

 public  boolean insert(int val){
    
        TreeNode parent = null;
        TreeNode node = new TreeNode(val);
        if(root == null){
    
           root = node;
           return true;
        }
        //root Not empty , It's not the first time to insert 
        TreeNode cur = root;
        while(cur != null){
    
            if(cur.val < val){
    
                parent = cur;
                cur = cur.right;
            }else if(cur.val == val){
    
                return false;
            }else{
    
                parent = cur;
                cur = cur.left;
            }
        }
        // After walking here ,cur = null, At this time, the insertion place is also found 
        if(parent.val < val){
    
            parent.right= node;
            cur = node;
        }else{
    
            parent.left = node;
            cur = node;
        }
        // Two way direction 
        node.parent = parent;
        // Finished inserting , You need to check the balance factor of relevant nodes , It is found that the balance factor of a node is incorrect , You need to rotate , And check upwards 
        while(parent != null){
    
            if(cur == parent.left){
    
                parent.bf--;
            }else{
    
                parent.bf++;
            }
            // Check whether the current balance factor meets 
            if(parent.bf == 0){
    
                // Because from parent Let's insert ,parent.bf It is most likely that dissatisfaction will lead to chain, leading to dissatisfaction above , If it is satisfied, there is no need to check up 
                break;
            }else if(parent.bf == 1 || parent.bf == -1){
    
                // The current is to meet , But the upward check is not necessarily satisfied 
                cur = parent;
                parent = cur.parent;
            }else{
    
                // At this point is not satisfied , Rotate directly , But I don't know which way to turn , We need to judge again 
                if(parent.bf == 2){
    
                    //parent.bf = 2, The description is the height of the right subtree of this node , Need to turn left , Then why should we judge again cur Well ???
                    // When we get here ,bf = 2, Illustrate this parent Here is the right node , There must be a node under the right node cur, Otherwise, it cannot be 2
                    // however cur We don't know whether your child is left or right , This also needs to be discussed 
                    if(cur.bf == 1){
    
                        //cur My child is right , left-handed 
                        rotateLeft(parent);
                    }else{
    
                        //cur.bf = -1  Right hand 
                        rotateRL(parent);
                    }
                }else{
    
                    //parent.bf = -2; The height of the left tree needs to be reduced 
                    if(cur.bf == 1){
    
                        rotateLR(parent);
                    }else{
    
                        rotateRight(parent);
                    }
                }
                break;
            }
        }
        return true;

    }

There are several situations about insertion , The situation that affects the balance factor is also different

This is in the cur Insert... To the right of the , The solution is left single rotation , because parent and cur The equilibrium factors of are all of the same number , Just one single spin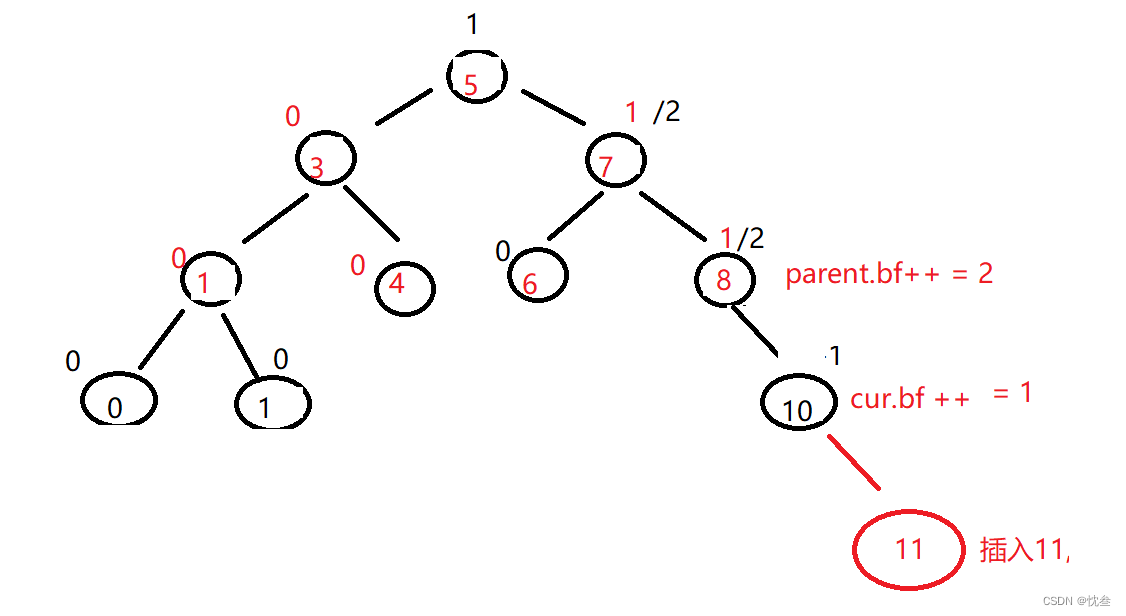

This is in the cur Insert... To the left of , The solution is right left double spin , because parent and cur The equilibrium factors of are all different , First right , But this right-handed node is not parent, It is parent.left
Turn left again parent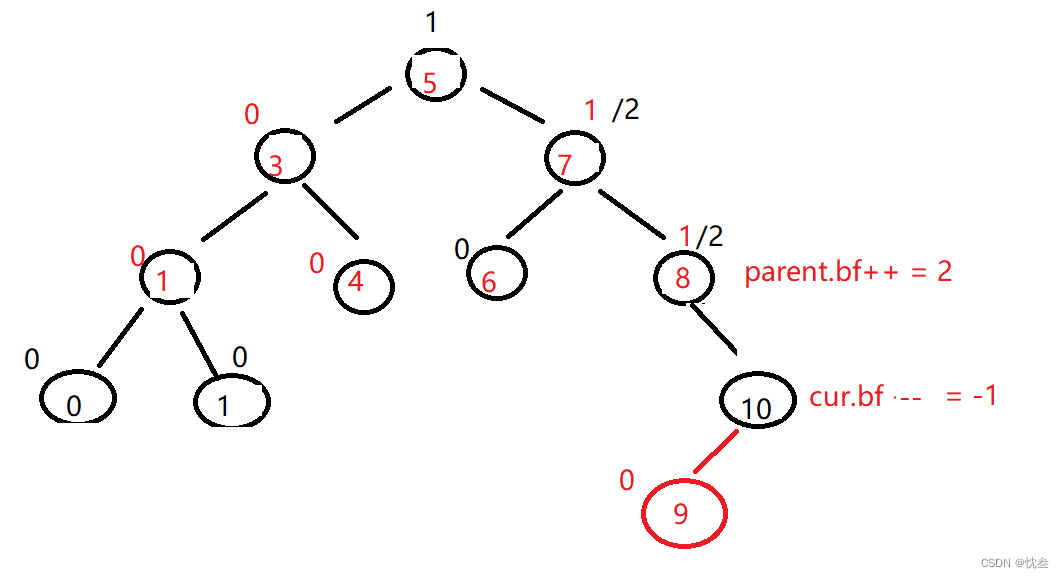

such parent.bf = -2, But from this, it can be divided into cur.bf = 1 perhaps -1, If the same number is introduced above, we can directly carry out a single rotation , And it can be right-handed , This situation is left-right double rotation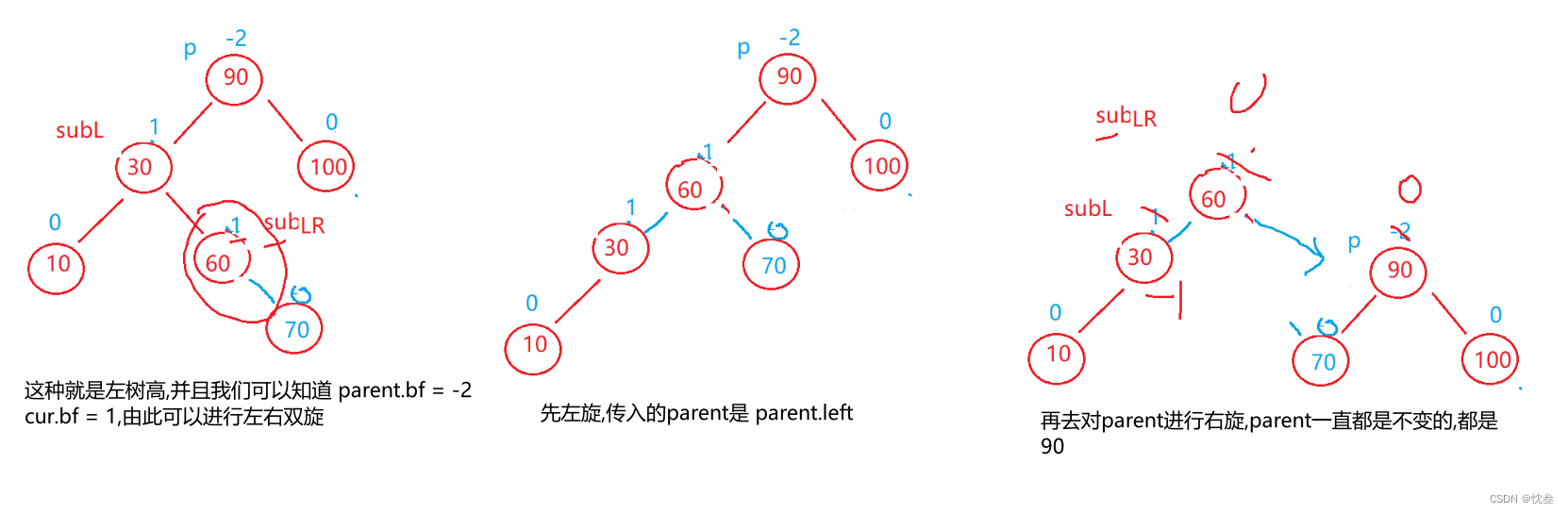

This is a single right rotation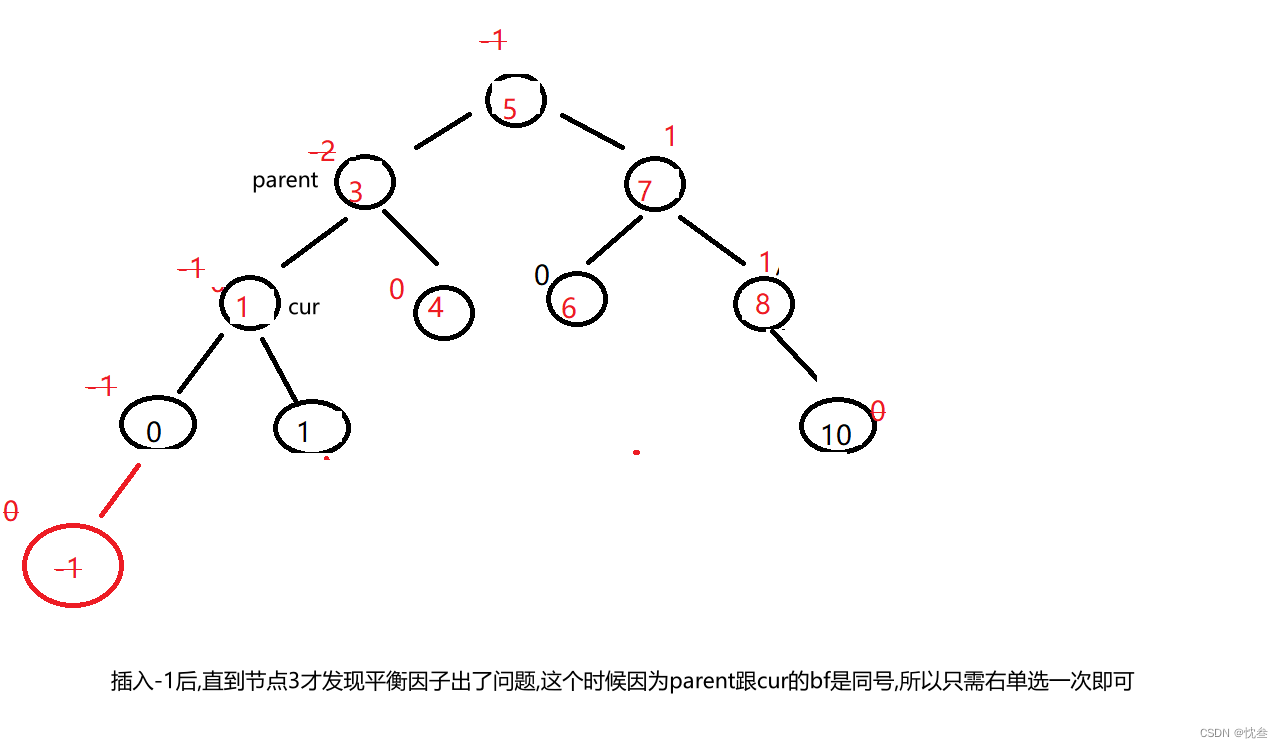

Left single spin code

public void rotateLeft(TreeNode parent) {
        TreeNode subR = parent.right;
        TreeNode subRL = subR.left;

        parent.right = subRL;

        subR.left = parent;
        if (subRL != null) {
            subRL.parent = parent;
        }
        TreeNode pParent = parent.parent;
        parent.parent = subR;
        if(root == parent){
            root  = subR;
            root.parent = null;
        }else{
            if(pParent.left == parent){
                pParent.left = subR;
            }else{
                pParent.right = subR;
            }
            subR.parent = pParent;
        }
        // After the rotation, I found , Of these two nodes bf  All are 0
        parent.bf = subR.bf = 0;
    }

Right single spin code

public void rotateRight(TreeNode parent) {
        // Right hand   Reduce the height of the left tree 
        TreeNode subL = parent.left;
        TreeNode subLR = subL.right;

        parent.left = subLR;
        subL.right = parent;

        // First judge whether there is subLR
        if (subLR != null) {
            // stay AVL Tree species , Yes parent So there are two-way references , There is already  parent.left = subRL, But there is still a need to back reference 
            // But we don't know subRL Existence does not exist , So we need to judge 
            subLR.parent = parent;
        }
        TreeNode pParent = parent.parent;
        parent.parent = subL;
        if (parent == root) {
            root = parent;
            root.parent = null;
        } else {
            if (parent == pParent.left) {
                subL = pParent.left;
            } else {
                subL = pParent.right;
            }
            subL.parent = pParent;
        }
        parent.bf = subL.bf = 0;
    }

Left and right double rotation code

 public void rotateLR(TreeNode parent){
         // First left and then right 
         TreeNode subL = parent.left;
         TreeNode subLR = subL.right;
         int bf = subLR.bf;
         rotateLeft(parent.left);
         rotateRight(parent);
         if(bf == -1) {
             subL.bf = 0;
             subLR.bf = 0;
             parent.bf = 1;
         }else if(bf == 1){
             subL.bf = -1;
             subLR.bf = 0;
             parent.bf = 0;
         }
     }

Right left double rotation

 public void rotateRL(TreeNode parent){
        // Right then left 
        TreeNode subR = parent.right;
        TreeNode subRL = subR.left;
        int bf = subRL.bf;
        rotateRight(parent.left);
        rotateLeft(parent);
        if(bf == -1) {
            subR.bf = 0;
            subRL.bf = 0;
            parent.bf = 1;
        }else if(bf == 1){
            subR.bf = -1;
            subRL.bf = 0;
            parent.bf = 0;
        }
    }