当前位置:网站首页>2021 Li Hongyi machine learning (1): basic concepts
2021 Li Hongyi machine learning (1): basic concepts
2022-07-05 02:38:00 【Three ears 01】
2021 Li hongyi machine learning (1): Basic concepts
B On the site 2021 Li Hongyi's learning notes of machine learning course , For reuse .
1 Basic concepts
Machine learning is ultimately about finding a function .
1.1 Different function categories
- Return to Regression—— Output is numeric
- classification Classification—— The output is in different categories classes, Do multiple choice questions
- Structural learning Structured Learning—— Generate a structured file ( Draw a picture 、 Write an article ), Let the machine learn to create
1.2 How to find functions (Training):
- First , Write a function with unknown parameters ;
- secondly , Definition loss( A function related to parameters ,MAE—— Absolute error ,MSE—— Mean square error );
- Last , Optimize , Find the loss Minimum parameters —— gradient descent
1) Randomly select the initial value of the parameter ;
2) Calculation ∂ L ∂ w ∣ w = w 0 \left.\frac{\partial L}{\partial w}\right|_{w=w^{0}} ∂w∂L∣∣w=w0, Then step down the gradient , The step size is l r × ∂ L ∂ w ∣ w = w 0 \left.lr\times\frac{\partial L}{\partial w}\right|_{w=w^{0}} lr×∂w∂L∣∣w=w0
3) Update parameters
This method has a huge drawback : Usually we will find Local minima, But what we want is global minima
1.3 Model
Linear model linear model There's a big limit , Cannot simulate polyline 、 Curve , This restriction is called model bias, So we need to improve .
How to improve :Piecewise Linear Curves
Many such sets can be fitted into curves .
1.3.1 sigmoid
It can be used sigmoid function y = c 1 1 + e − ( b + w x 1 ) = c s i g m o i d ( b + w x 1 ) y=c \frac{1}{1+e^{-\left(b+w x_{1}\right)}}=c sigmoid(b+wx_1) y=c1+e−(b+wx1)1=csigmoid(b+wx1) Fit the blue broken line :
y = b + ∑ i c i sigmoid ( b i + ∑ j w i j x j ) y=b+\sum_{i} c_{i} \operatorname{sigmoid}\left(b_{i}+\sum_{j} w_{i j} x_{j}\right) y=b+i∑cisigmoid(bi+j∑wijxj)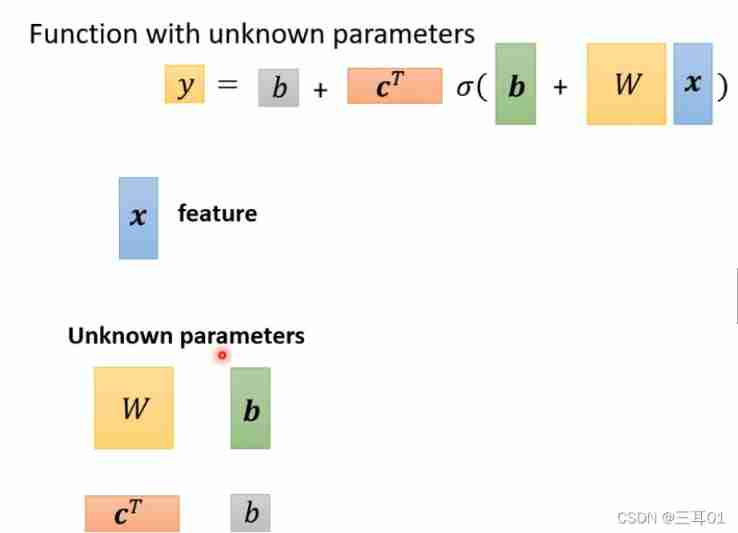
All unknown parameters in this , Use both θ \theta θ Express :
Use all at once θ \theta θ To calculate , Make a gradient descent , Such a large amount of data , Therefore, small batches are used batch: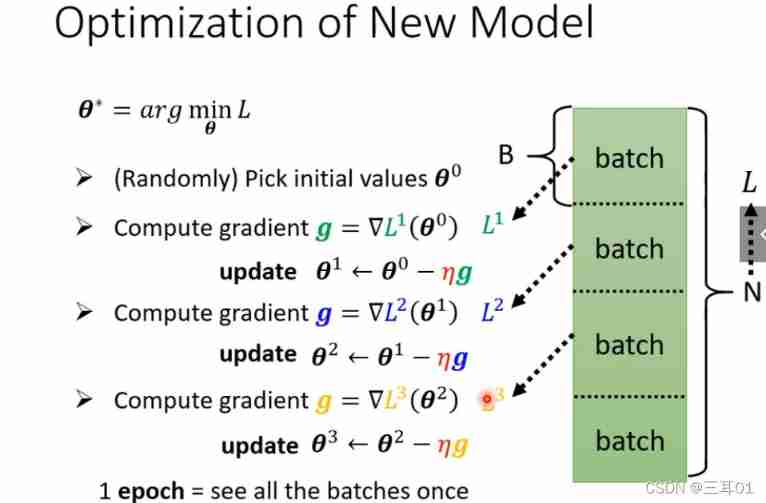
every last data The number of updates depends on the total amount of data and batch Number :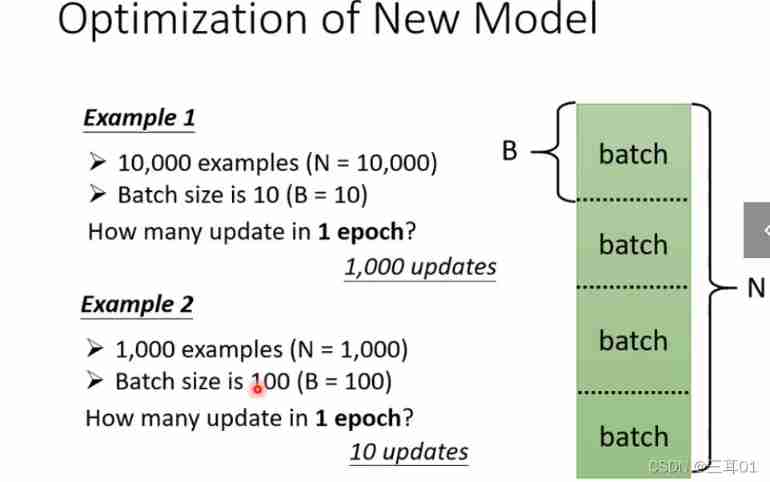
1.3.2 ReLU
In front of it is soft sigmoid, That's the curve , In fact, you can use two ReLU Quasi synthesis hard sigmoid, That's the broken line :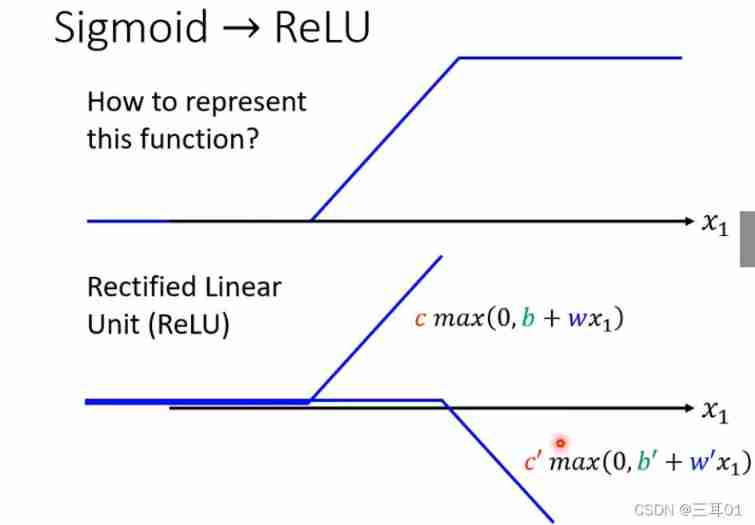
above sigmoid The formula becomes :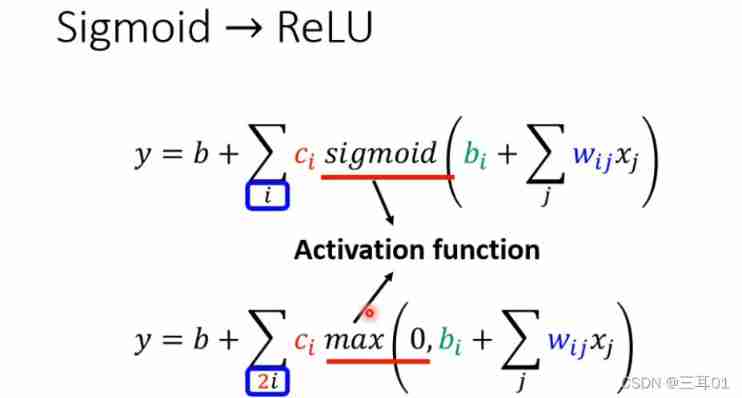
1.3.3 Yes sigmoid The calculation of can be done several more times
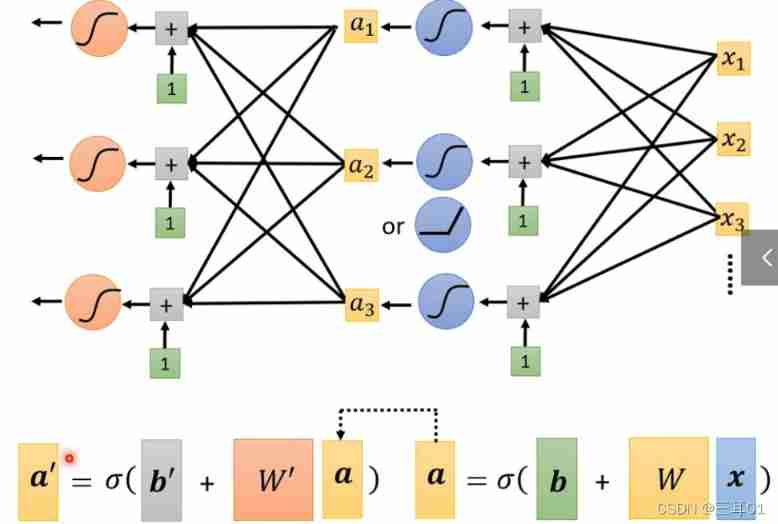
There are many such layers , It is called neural network Neural Network, Later called Deep learning=Many hidden layers
边栏推荐
- STL container
- 官宣!第三届云原生编程挑战赛正式启动!
- ELFK部署
- ASP. Net core 6 framework unveiling example demonstration [01]: initial programming experience
- RichView TRVStyle MainRVStyle
- Go RPC call
- Richview trvunits image display units
- Introduce reflow & repaint, and how to optimize it?
- Spark SQL learning bullet 2
- 使用druid連接MySQL數據庫報類型錯誤
猜你喜欢
Design and implementation of community hospital information system
The steering wheel can be turned for one and a half turns. Is there any difference between it and two turns

Can you really learn 3DMAX modeling by self-study?
![[uc/os-iii] chapter 1.2.3.4 understanding RTOS](/img/33/1d94583a834060cc31cab36db09d6e.jpg)
[uc/os-iii] chapter 1.2.3.4 understanding RTOS
Spark SQL learning bullet 2

Android advanced interview question record in 2022

Missile interception -- UPC winter vacation training match
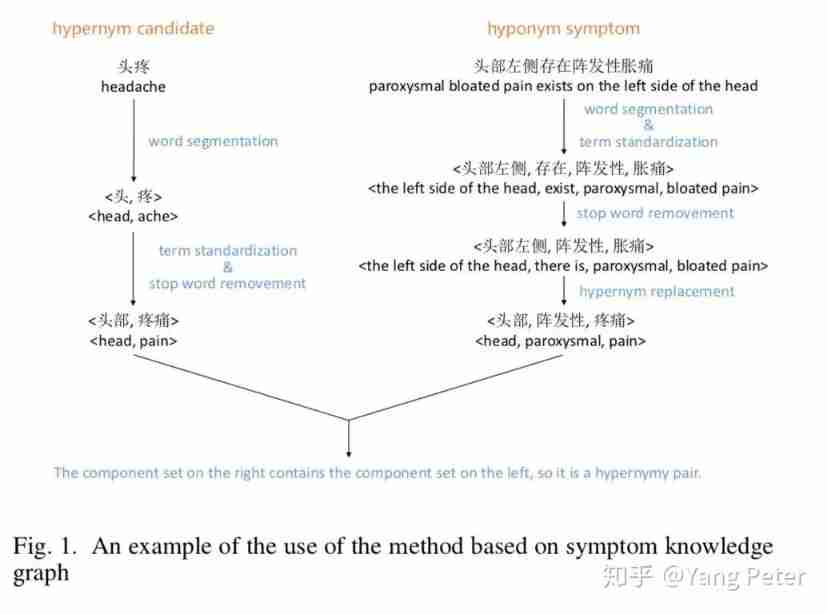
Exploration of short text analysis in the field of medical and health (I)
如何做一个炫酷的墨水屏电子钟?

Action News
随机推荐
openresty ngx_lua執行階段
Zabbix
Exploration of short text analysis in the field of medical and health (I)
8. Commodity management - commodity classification
Go RPC call
Structure of ViewModel
Start the remedial work. Print the contents of the array using the pointer
ASP. Net core 6 framework unveiling example demonstration [01]: initial programming experience
Privatization lightweight continuous integration deployment scheme -- 01 environment configuration (Part 1)
Introduce reflow & repaint, and how to optimize it?
Abacus mental arithmetic test
Word processing software
Learn game model 3D characters, come out to find a job?
D3js notes
The perfect car for successful people: BMW X7! Superior performance, excellent comfort and safety
The phenomenology of crypto world: Pioneer entropy
He was laid off.. 39 year old Ali P9, saved 150million
TCP security of network security foundation
. Net starts again happy 20th birthday
Tucson will lose more than $400million in the next year