当前位置:网站首页>Discussion on the dimension of confrontation subspace
Discussion on the dimension of confrontation subspace
2022-07-05 04:24:00 【PaperWeekly】

PaperWeekly original · author | Sun Yudao
Company | Beijing University of Posts and telecommunications
Research direction | GAN Image generation 、 Emotional confrontation sample generation

introduction
Confronting samples is one of the main threats of deep learning models , Confrontation samples will make the target classifier model classification error, and it exists in the dense confrontation subspace , The antagonism subspace is contained in a specific sample space . This paper mainly discusses the dimension of antagonism subspace , That is, for a specific sample of a single model, what is the dimension of the subspace , What is the dimension of the subspace against a specific sample of multiple models .

Antagonism subspace
Given a clean sample , And its corresponding label , With parameters The neural network classifier of is , The loss function is , The confrontation sample is , Then according to the multivariate Taylor expansion :
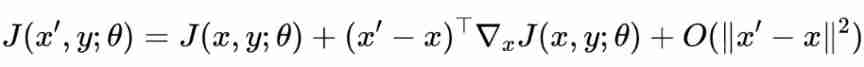
Further, the optimization objective is :
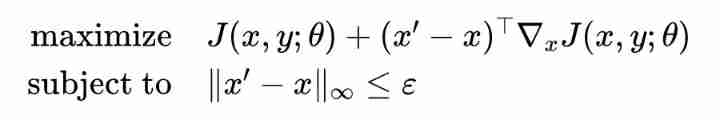
Further, the calculation formula of the countermeasure sample is :
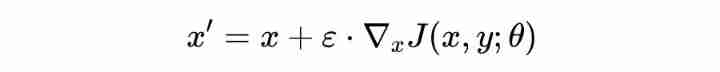
among It indicates the size of the counter disturbance . It can be seen from the above formula that , Clean samples Along the gradient You can enter the confrontation subspace . Further details are shown in the figure below , Among them (a),(b) and (c) It represents the result diagram of the classifier classification given a clean sample generated in different directions , Each square represents the classification result of each sample , White in the square indicates that the classifier is classified correctly , Color means that the classifier is classified into other different categories . chart (d),(e) and (f) Decomposition diagram showing the direction of sample movement .
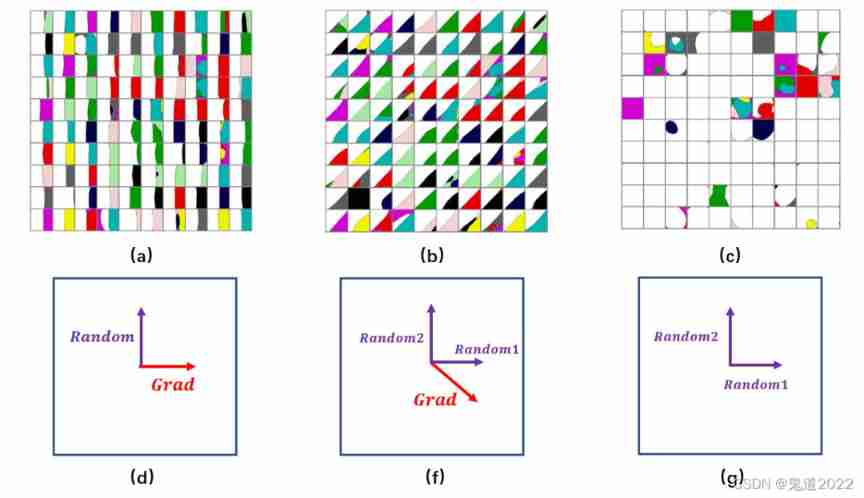
From above (d) You know , If you choose two orthogonal directions , One is the gradient direction against disturbance , The other is the direction of random disturbance , From the picture (a) You know , Clean samples along the anti disturbance direction can enter the anti disturbance subspace , Along the direction of random disturbance, no countermeasure samples are generated . From above (e) You know , If these two orthogonal directions are at an angle to the gradient direction , From the diagram (b) It can be seen that these two orthogonal directions can enter the confrontation subspace , But it's not the fastest direction . From above (f) You know , If these two orthogonal directions are random disturbances , From the picture (c) You know , It is difficult for clean samples to enter the confrontation subspace , The misclassification of the figure is independent of the confrontation samples , It is related to the training of the model itself .

Single model antagonism subspace dimension
From the multivariate Taylor expansion of the loss function against samples in the previous section, we can approximate :
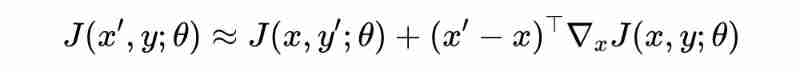
Among them, the order is ,. The purpose is to explore a given model , Solve the anti disturbance Make the model loss function grow at least We have to confront the problem of subspace dimension , The mathematical expression is :
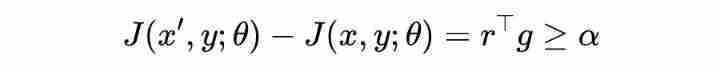
among , Disturbance Belong to this In the confrontation subspace composed of orthogonal vectors , It's against the dimension of subspace . At this point, the following theorem holds , The detailed proof process is as follows :
Theorem 1: Given and , Maximum antagonism subspace dimension Orthogonal vector of Satisfy , If and only if .
prove :
Proof of necessity : It is known that and , Make , also It is orthogonal. , Thus we can see that .
1. If , Then we can know from the vector product formula :
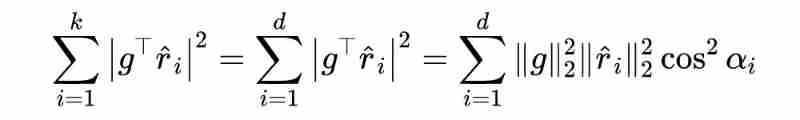
among , It's a vector and Cosine of , And I know , So there is :
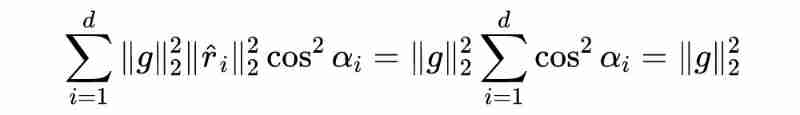
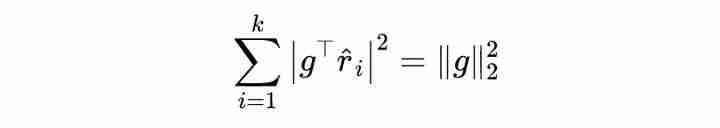
2. If , First of all Orthogonal expansion , Expand to :
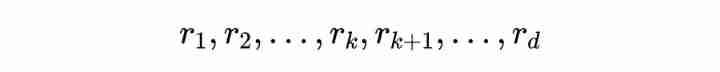
Then we can see :
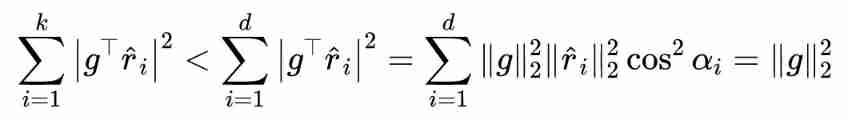
Then we can know :
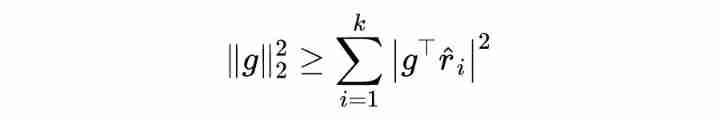
Again because , So there is :
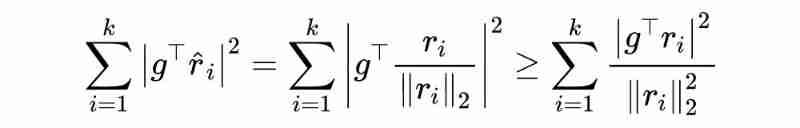
because ,, So there is :
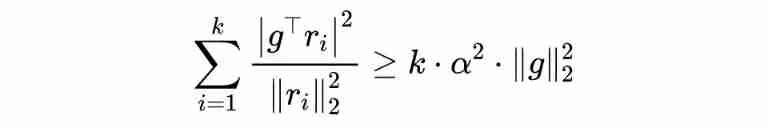
Again because :
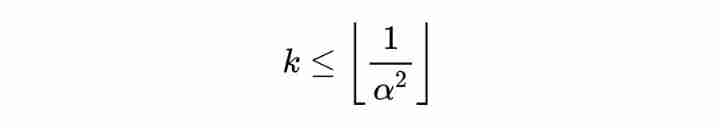
finally :
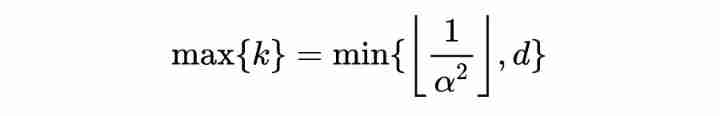
Sufficiency proof :
It is known that , Make It means Base vector of , Is a rotation matrix and has .
Make , also For the rotation matrix , So there is :
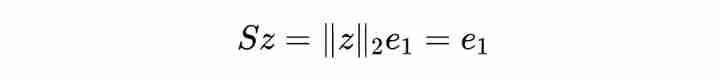
Easy to know , matrix For the rotation matrix , Its satisfaction :
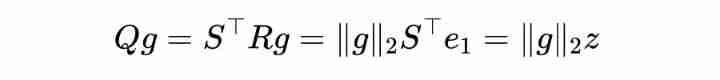
Let vector , also , among It's a matrix Of the Column , It's an orthogonal matrix , Then we can know :
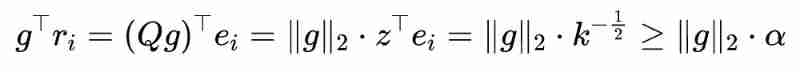
Certificate completion !
Through the above proof, we can get a very rigorous and beautiful conclusion , That is, against the dimension of subspace Size and growth degree of loss function Is inversely proportional to the square of , This is also very intuitive . The greater the growth , The more the antagonism subspace collapses towards the gradient , Because the gradient direction is the fastest direction .

Multi model antagonism subspace dimension
In the black box model , It often takes advantage of the mobility of the counter samples to attack , That is, use the model Generated countermeasure samples , Migrate unknown classification model Attack in , The main reason is that there are overlapping confrontation subspaces for two different models , Therefore, it can make the anti sample have the mobility of attack .
Assume It's a sample For the model Makes its loss function grow To counter disturbance ; It's a sample For the model Makes its loss function grow To counter disturbance . among , Disturbance Belong to this In the confrontation subspace composed of orthogonal vectors . among , Disturbance Belong to this In the confrontation subspace composed of orthogonal vectors ; At this time, the size of the subspace dimension against multiple models is :
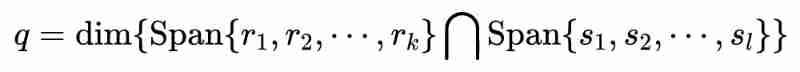
Similarly, according to the above derivation ideas, we can find 3 Dimensions of confrontation subspaces with more than models overlapping .
Thank you very much
thank TCCI Tianqiao Academy of brain sciences for PaperWeekly Support for .TCCI Focus on the brain to find out 、 Brain function and brain health .
Read more

# cast draft through Avenue #
Let your words be seen by more people
How to make more high-quality content reach the reader group in a shorter path , How about reducing the cost of finding quality content for readers ? The answer is : People you don't know .
There are always people you don't know , Know what you want to know .PaperWeekly Maybe it could be a bridge , Push different backgrounds 、 Scholars and academic inspiration in different directions collide with each other , There are more possibilities .
PaperWeekly Encourage university laboratories or individuals to , Share all kinds of quality content on our platform , It can be Interpretation of the latest paper , It can also be Analysis of academic hot spots 、 Scientific research experience or Competition experience explanation etc. . We have only one purpose , Let knowledge really flow .
The basic requirements of the manuscript :
• The article is really personal Original works , Not published in public channels , For example, articles published or to be published on other platforms , Please clearly mark
• It is suggested that markdown Format writing , The pictures are sent as attachments , The picture should be clear , No copyright issues
• PaperWeekly Respect the right of authorship , And will be adopted for each original first manuscript , Provide Competitive remuneration in the industry , Specifically, according to the amount of reading and the quality of the article, the ladder system is used for settlement
Contribution channel :
• Send email :[email protected]
• Please note your immediate contact information ( WeChat ), So that we can contact the author as soon as we choose the manuscript
• You can also directly add Xiaobian wechat (pwbot02) Quick contribution , remarks : full name - contribute

△ Long press add PaperWeekly Small make up
Now? , stay 「 You know 」 We can also be found
Go to Zhihu home page and search 「PaperWeekly」
Click on 「 Focus on 」 Subscribe to our column
·

边栏推荐
- Moco is not suitable for target detection? MsrA proposes object level comparative learning target detection pre training method SOCO! Performance SOTA! (NeurIPS 2021)...
- About the project error reporting solution of mpaas Pb access mode adapting to 64 bit CPU architecture
- TPG x AIDU|AI领军人才招募计划进行中!
- 【thingsboard】替换首页logo的方法
- A solution to the problem that variables cannot change dynamically when debugging in keil5
- How to carry out "small step reconstruction"?
- Sequence diagram of single sign on Certification Center
- Function (error prone)
- Threejs factory model 3DMAX model obj+mtl format, source file download
- 长度为n的入栈顺序的可能出栈顺序种数
猜你喜欢
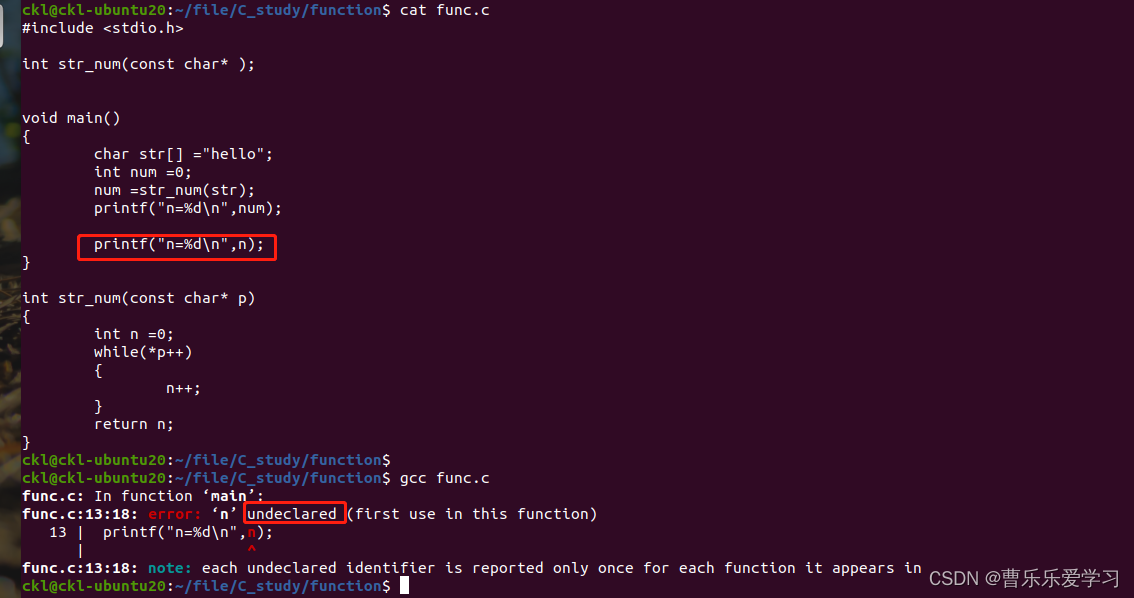
Function (basic: parameter, return value)

如何优雅的获取每个分组的前几条数据

基于TCP的移动端IM即时通讯开发仍然需要心跳保活

如何实现实时音视频聊天功能
“金九银十”是找工作的最佳时期吗?那倒未必
level18
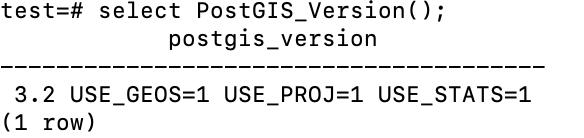
MacBook安装postgreSQL+postgis
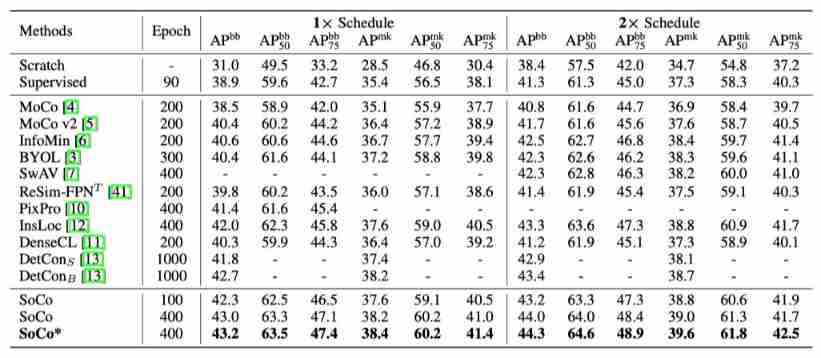
Moco is not suitable for target detection? MsrA proposes object level comparative learning target detection pre training method SOCO! Performance SOTA! (NeurIPS 2021)...
Burpsuite grabs app packets

首席信息官如何利用业务分析构建业务价值?
随机推荐
Sequence diagram of single sign on Certification Center
A應用喚醒B應該快速方法
官宣!第三届云原生编程挑战赛正式启动!
Network security - record web vulnerability fixes
MacBook installation postgresql+postgis
Ffmepg usage guide
After the deployment of web resources, the navigator cannot obtain the solution of mediadevices instance (navigator.mediadevices is undefined)
SPI read / write flash principle + complete code
Introduction to RT thread kernel (4) -- clock management
程序员应该怎么学数学
How to remove installed elpa package
A application wakes up B should be a fast method
[untitled]
Is there a sudden failure on the line? How to make emergency diagnosis, troubleshooting and recovery
[uniapp] system hot update implementation ideas
Bit operation skills
Looking back on 2021, looking forward to 2022 | a year between CSDN and me
[phantom engine UE] the difference between running and starting, and the analysis of common problems
[illusory engine UE] method to realize close-range rotation of operating objects under fuzzy background and pit recording
Function (basic: parameter, return value)


