当前位置：网站首页>I-BERT

I-BERT

2022-07-06 08:57:00 【cyz0202】

background

In this paper, ICML2021 I-BERT: Integer-only BERT Quantization

The purpose of this article is to BERT Perform more thorough quantization and integer calculations ;

The author believes that the previous quantitative scheme is not right gelu、softmax These nonlinear operations are quantified （ Here's the picture 1）, That is to keep float Type of calculation , Not only affects the computational efficiency , And it cannot be deployed on some chips that only support integer Computing ;

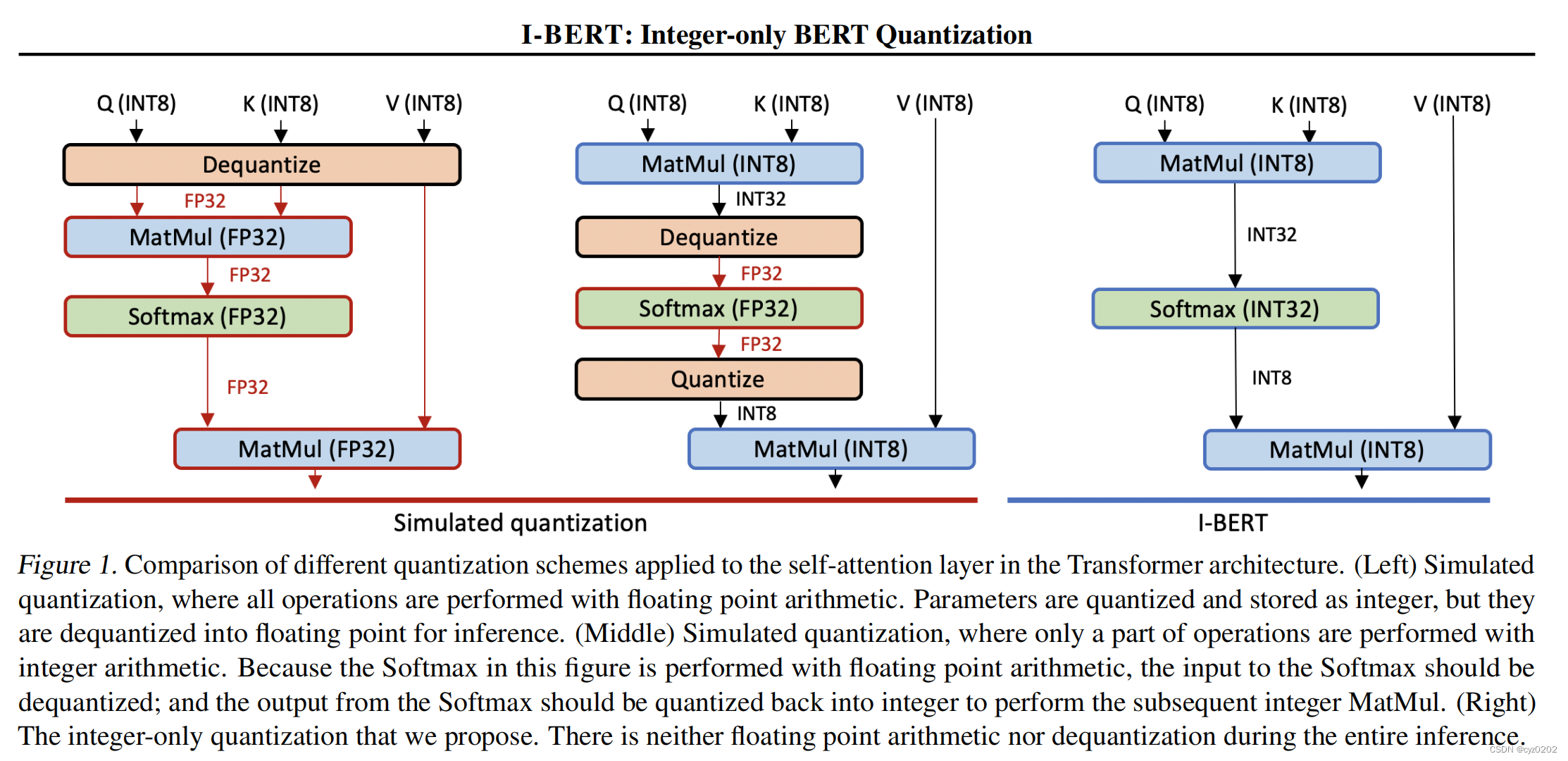
The quantitative scheme adopted by the author is 8bits Symmetric quantization ;

Existing schemes and deficiencies

The author mainly solves GELU、softmax The quantization problem of these two kinds of nonlinear layers ;

First look at it. GELU The expression of , as follows ,erf go by the name of error function

$\\GELU(x) = x*\frac{1}{2}[1+erf(\frac{x}{\sqrt2})]$

among $\\ erf=\frac{2}{\sqrt\pi}\int^x_0e^{-t^2}dt \in [-1, 1] \\$

And $\\ \int^{\infty }_0e^{-t^2}dt = \frac{\sqrt{\pi}}{2}$

GELU It is difficult to quantify directly , Forced quantization will lead to a large loss of accuracy ;

Unlike linear layers （ Such as matrix product 、 Piecewise linear RELU etc. ）, The linear property can be used to inverse quantize to float The result of the calculation is （ The author gives an example MatMul(Sq) = S*MatMul(q), among x=Sq,S by scale,q by x Quantized value of ）;

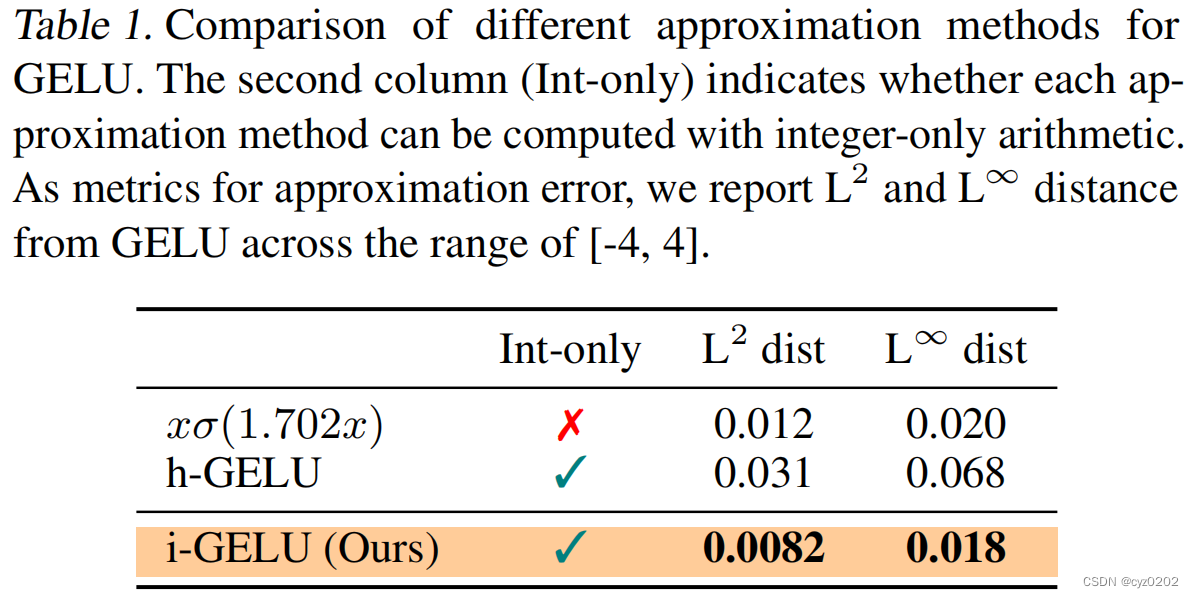
Some existing approximations GELU The plan , Include ：

- sigmoid The approximate , as follows , Introduce nonlinearity sigmoid, It's still not good for integer calculation

$\\ GELU(x) = x\sigma(1.702x)\\ where \space\ \sigma(x) = sigmoid(x)$

- ReLU6 The approximate , as follows , Use ReLU6, Although it can be integer , But it didn't work ; The program is also known as h-GELU

$h-GELU(x) := x\frac{ReLU6(1.702x+3)}{6} \approx GELU(x)$

The figure below 2 The picture on the left shows h-GELU The shortcomings of

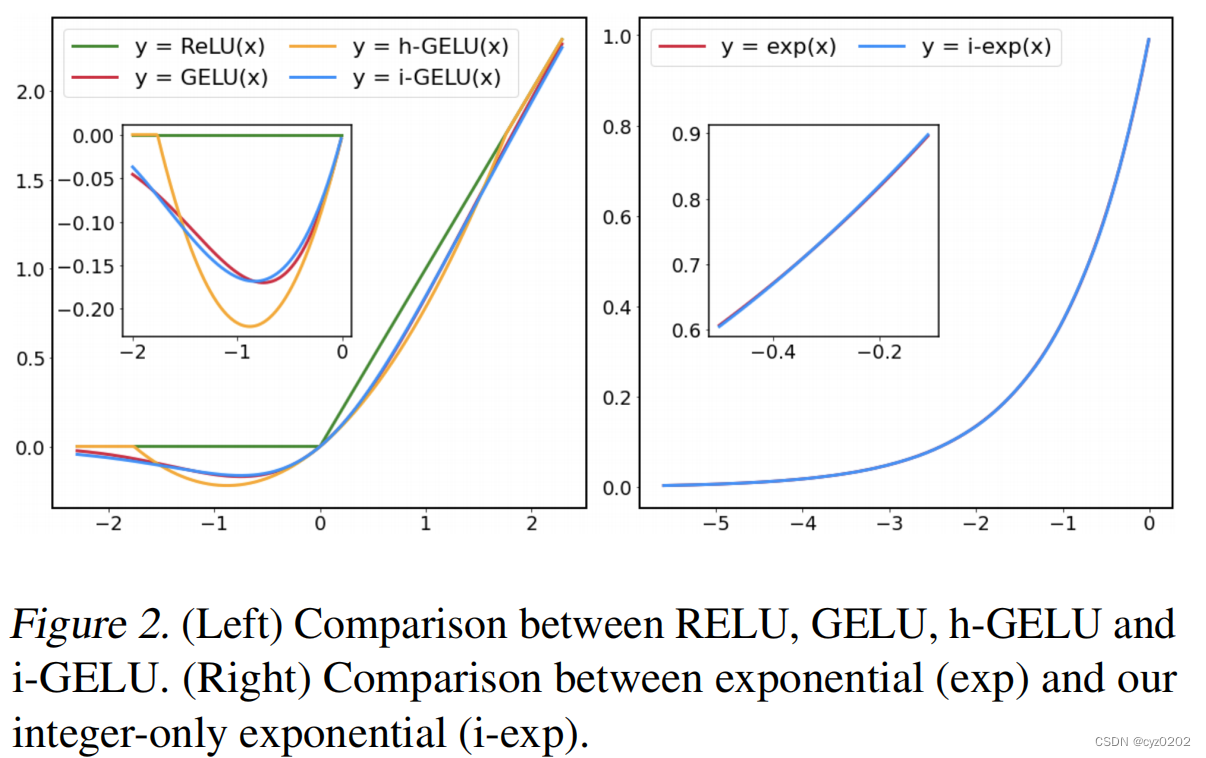
chart 2： Comparison of several activation functions and exponential functions before and after quantification

GELU Solutions for

By analyzing , It is considered that second-order polynomial pairs can be introduced erf Make an approximation , Further to GELU Make an approximation , The calculation method is as follows

$\\\underset{a,b,c}{min}\frac{1}{2}||GELU(x) - x*\frac{1}{2}[1+L(\frac{x}{\sqrt2})]||^2_2\\ s.t. \space\ \space\ \space\ L(x) = a(x+b)^2 + c$

This idea comes from the theory that any function can be fitted by polynomial function , This type of polynomial is called interpolating polynomials（ Interpolation polynomial ）; For details, please move to the original ;

The result obtained by directly optimizing the above formula is not ideal , as a result of erf The definition domain of is a real domain scope ;

in consideration of erf The value range of is [-1, 1], And erf It's an odd function , namely

erf(-x) = -erf(x)

Therefore, the author designs the positive real number field part , And extended to negative real number field , Get the following L(x),

$\\L(x) = sgn(x)*\{a*[clip(|x|, max=-b) + b]^2 + 1\}$ , among

$\\ a=-0.2888 \\b= -1.769$

clip Medium max Express |x| The maximum value is -b;

therefore $L(x) \in [-1, 1]$ , And it is an odd function ;

a、b By looking for some GELU To solve the fitting problem ;

As can be seen from the above ,

$i-GELU(x) := x*\frac{1}{2}[1 + L(\frac{x}{\sqrt2})]$

i-GELU Quantitative scheme of

With GELU Polynomial expression of , You can start designing quantitative solutions ;

L(x) It's a polynomial , So you have to know how to quantize polynomials first ;

The author gives a polynomial Quantization Algorithm I-POLY, as follows

chart 3： Polynomial Quantization Algorithm I-POLY

Can verify $q_{out}S_{out} \approx a(x+b)^2 + c$ ,

So arbitrary 2 Quantization of order polynomials 、 The above algorithm can be used for inverse quantization ;

（ notes ： I feel that the quantification here belongs to a kind of quantification for calculating quantification ; The calculation process is ok , The feeling is deliberately constructed ,q_out and S_out Are not necessarily the real quantized values of polynomial results and scale）

------

With the polynomial quantization method , You can continue to realize I-GELU The quantitative scheme of , The calculation process is as follows

chart 4：I-GELU The implementation of the

The call stack is I-GELU -> I-ERF -> I-POLY

Pay attention to the picture 4 Some implementation tips in the algorithm , Such as

$\frac{x}{\sqrt2} = q * \frac{S}{\sqrt2}$ ,

$\\x' \\= clip(|x|, max=-b) \\ = S * clip(|q|, max=-b/S) \\= S*q'$

Notice the above formula max=-b/S, It may have to be changed to max=round(-b/S), Otherwise q’ There is no guarantee that it is integer ...

------

The above is the I-GELU Implementation process , The effect is as follows

SOFTMAX Solutions for

- Use higher-order polynomials for approximation , Available scenarios are limited ;

SOFTMAX Quantitative scheme of

For numerical stability , The author first gives a brief introduction to softmax To deal with , as follows

$Softmax(\vec{x})_i = \frac{e^{x_i - x_{max}}}{\sum^{k}_{j=1}e^{x_j - x_{max}}}$

$x_{max} = max_i(\vec{x})$

It is worth mentioning that , $\tilde{x} = x_i - x_{max} < 0$

For a non positive real number $\tilde{x}$ , It can be approximated by the following formula

$\tilde{x} = -ln2*z + p$

among z（ merchant ） Is a non negative integer ,p（ remainder ） Value range (-ln2, 0] ;

Then there are

$e^{\tilde{x}} = 2^{-z}*e^p = e^p>> z$

Upper form >> Indicates the right shift operation ;

further , If you can e^p Expressed as integer calculation , Then it can be used for all $e^{\tilde{x}}$ as well as Softmax Perform integer calculation ;

and e^p in p Value range of relative x perhaps $\tilde{x}$ Much smaller , It can be approximated better ;

To recall GELU, The author proposes to adopt 2 Order polynomial approximates nonlinear function ; You can do the same here ;

Author search e^p The method of approximating second-order polynomials , It is through (-ln2, 0] Calculate the optimal solution of the following formula in the range ：

$\\\underset{a,b,c}{min}||e^p - L(p)||^2_2 \\s.t. \space\ \space\ L(p) = a(p+b)^2+c$

The resulting

L(p) = 0.3585(p+1.353)^2 + 0.344

$i-exp(\tilde{x}) := L(p)>> z$

among $z = \left \lfloor \frac{\tilde{x}}{-ln2} \right \rfloor$ , $p = \tilde{x} + ln2*z$

chart 2 The figure on the right shows that the above approximation has a good effect ;

Quantitative calculation method of polynomials I-POLY It has been introduced above , So the whole thing Softmax The quantitative calculation method of is