Detailed explanation of dynamic planning

Preface

The steps of algorithm implementation

1、 Create a one-dimensional array or two-dimensional array , Save the results of each sub problem , Whether to create a one-dimensional array or a two-dimensional array depends on the subject , Basically, if the title gives a one-dimensional array to operate , You can just create a one-dimensional array , If the title gives two one-dimensional arrays to operate or two different types of variable values , For example, the volume and total volume of different objects in knapsack problem , Different denominations of change and the total amount of money in the change problem , In this way, you need to create a two-dimensional array .

notes ： Creating a two-dimensional array requires a two-dimensional solution , You can create a one-dimensional array and use the rolling array to solve , That is, the values in a one bit array keep changing , I will describe it in detail later

2、 Set array boundary value , One dimensional array is to set the first number , A two-dimensional array is to set the values of the first row and the first column , In particular, scrolling a one-dimensional array is to set the value of the whole array , Then according to the following different data, it will be added and changed into different values .

3、 Find the state transition equation , In other words, find the relationship between each state and its previous state , Write the code according to the state transformation equation .

4、 Returns the desired value , It is usually the last of the array or the bottom right corner of the two-dimensional array .

One 、 Dynamic programming solution

The core design idea of dynamic programming is mathematical induction .

⾸ First , The dynamic programming problem is ⼀ The general form is to seek the maximum value . Dynamic programming is actually an operation research ⼀ It's an optimization ⽅ Law , Just ask on the computer Answer on the question ⽤⽐ More , ⽐ Let's ask for the best ⻓ Increasing ⼦ Sequence , most ⼩ Edit distance and so on .
secondly , The kernel of dynamic programming ⼼ The problem is exhaustion . Because the requirements are the most valuable , Be sure to put all available ⾏ The answer to this question is exhaustive , Then find the best value .

however , The exhaustion of dynamic programming is a little special , Because there are problems like this 「 overlap ⼦ problem 」 , If it's violent ⼒ Exhaustively, the efficiency will be extremely low , So we need to 「 Memorandum 」 perhaps 「DP table」 To optimize the exhaustion process , Avoid unnecessary calculations .⽽ And , Dynamic programming problem ⼀ There will be 「 The optimal ⼦ structure 」, Can pass ⼦ The best value of the problem is the best value of the original problem .

in addition , Although the core of dynamic programming ⼼ Thought is to seek the best value , But the problem can change in a thousand ways , All available resources are listed ⾏ The solution is not ⼀ Pieces of Easy things , Only list the right ones 「 State shift ⽅ cheng 」 , In order to correctly exhaust . As mentioned above overlap ⼦ problem 、 The optimal ⼦ structure 、 State shift ⽅ Process is the three elements of dynamic programming . What do you mean? I'll give you an example , But in practical algorithmic problems , Write state transitions ⽅ Cheng is the most difficult , This is why many friends find dynamic planning difficult Why ,

Two 、 Templates

no

3、 ... and 、 practice

931. The descent path is the smallest and （ secondary ）

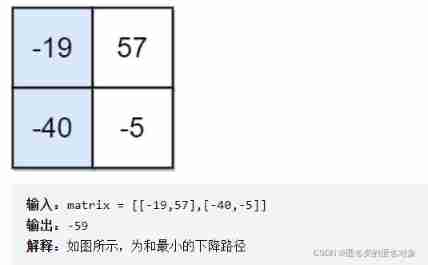
1、 Be clear about status and choice ： The status is matrix【i】【j】 The minimum sum of the descent paths of . With the progress of Dynamic Planning ,i from 0 To row,j from 0 To col. Each state has three different choices , Go straight down （i+1,j）, lower left （i+1,j-1） And lower right （i+1,j+1）.
2、 Determine according to the status dp Array ： Determine according to the status ,dp【i】【j】 It is defined as matrix【i】【j】 Is the minimum sum of the descending path at the end .
3、 Determine the state transition equation according to the selection ： There are three options for each state ,dp【i】【j】=matrix【i】【j】+min{dp【i-1】【j】,dp【i-1】【j-1】,dp【i-1】【j+1】},i∈【0】【row】,j∈【0】【col】
4、 determine base case： according to dp Array definition and state transition equation , Just make sure dp The upper layer of the array , You can determine each state of the next layer .

class Solution {
    
     public int minFallingPathSum(int[][] matrix) {
    
        int row = matrix.length;
        int col = matrix[0].length;
        //dp[i][j]: With matrix[i][j] The descending path at the end is the minimum sum 
        int[][] dp = new int[row][col];
        //base case
        for (int j = 0; j < col; j++) {
    
            dp[0][j] = matrix[0][j];
        }
      
        for (int i = 1; i < row; i++) {
    
            for (int j = 0; j < col; j++) {
    
                int left = 0, right = 0;//left It stands for the upper left ,right It stands for the upper right ,up It means right above 
                int up = dp[i - 1][j];
                if (j - 1 < 0) {
    	// Because compare the minimum , It is set to int The maximum of 
                    left = Integer.MAX_VALUE;
                } else {
    
                    left = dp[i - 1][j - 1];	
                }
                if (j + 1 >= col) {
    		// Same as left
                    right = Integer.MAX_VALUE;
                } else {
    
                    right = dp[i - 1][j + 1];
                }
                 // State transition equation 
                dp[i][j] = matrix[i][j] + Math.min(left, Math.min(right, up));
            }
        }
        int res = Integer.MAX_VALUE;
        // Traverse the array to find the minimum 
        for (int j = 0; j < col; j++) {
    
            res = Math.min(res, dp[row - 1][j]);
        }
        return res;
    }
}

1289. The descent path is the smallest and II（ difficult ）

n For the number of lines ,m Represents the number of columns .
1、 States and transitions ： The state refers to the minimum sum of the descent paths of each different subscript ; The transfer points to the next line transfer （ Except for the same column ）.
2、dp Array ： According to the State ,dp[i][j] Referring to matrix[i][j] The descending path at the end is the minimum sum .
3、 State transition equation ： According to the transfer ,dp【i】【j】=min{dp【i-1】【k】}, among ,k∈【0,m】&k！=j.
4、base case： According to the state and transition , got it dp The first row of the array can calculate the remaining elements .

class Solution {
    
   public int minFallingPathSum(int[][] matrix) {
    
        int n = matrix.length;
        int m = matrix[0].length;
        //dp[i][j]: With matrix[i][j] The descending path at the end is the minimum sum 
        int[][] dp = new int[n][m];
        //base case
        for (int j = 0; j < m; j++) {
    
            dp[0][j] = matrix[0][j];
        }
        for (int i = 1; i < n; i++) {
    
            for (int j = 0; j < m; j++) {
    
                dp[i][j] = Integer.MAX_VALUE;
                for (int k = 0; k < m; k++) {
    
                    int temp;
                    if (k < 0 || k >= m || j == k) {
        // Because compare the minimum , It is set to int The maximum of 
                        temp = Integer.MAX_VALUE;
                    } else {
    
                        temp = dp[i - 1][k];
                    }
                    dp[i][j] = Math.min(dp[i][j], temp);
                }
                dp[i][j] += matrix[i][j];
            }
        }
        int res = Integer.MAX_VALUE;
        // Traverse the array to find the minimum 
        for (int j = 0; j < m; j++) {
    
            res = Math.min(res, dp[n - 1][j]);
        }
        return res;
    }
}

The finger of the sword Offer II 099. Sum of minimum paths （ secondary ）

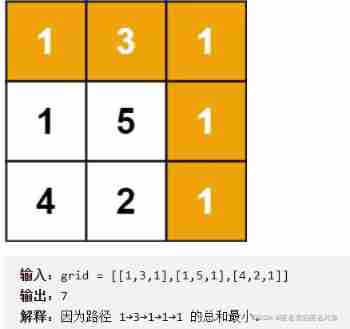
1、 States and transitions ： State refers to the minimum path sum of each different subscript . Transition means that there are two choices for each state , Down or left .
2、dp Array ： According to the State ,dp[i][j] Referring to grid【i】【j】 The sum of the minimum paths at the end .
3、 State transition equation ： According to the transfer ,dp【i】【j】=min{dp【i-1】【j】,dp【i】【j-1】}+grdi【i】【j】.
4、base case： Know the first row and the first column dp, You can launch all dp.

class Solution {
    
    public int minPathSum(int[][] grid) {
    
        int n = grid.length, m = grid[0].length;
        int[][] dp = new int[n][m];   //dp[i][j]: With grid【i】【j】 The sum of the minimum paths at the end 
        //base case
        dp[0][0] = grid[0][0];
        for (int i = 1; i < n; i++) {
    
            dp[i][0] = dp[i - 1][0] + grid[i][0];
        }
        for (int j = 1; j < m; j++) {
    
            dp[0][j] = dp[0][j - 1] + grid[0][j];
        }
        // State shift 
        for (int i = 1; i < n; i++) {
    
            for (int j = 1; j < m; j++) {
    
                dp[i][j] = grid[i][j] + Math.min(dp[i - 1][j], dp[i][j - 1]);
            }
        }
        return dp[n - 1][m - 1];
    }
}

The finger of the sword Offer II 100. The sum of the smallest paths in a triangle ( secondary )

Different from the previous question, the number of columns in this question will change , Each state can be moved down and down right .

class Solution {
    
    public int minimumTotal(List<List<Integer>> triangle) {
    
        int n = triangle.size();
        int[][] dp = new int[n][triangle.get(n - 1).size()];
        for (int i = 0; i < n; i++) {
    
            Arrays.fill(dp[i], Integer.MAX_VALUE);
        }
        dp[0][0] = triangle.get(0).get(0);
        for (int i = 1; i < n; i++) {
    
            dp[i][0] = dp[i - 1][0] + triangle.get(i).get(0);
        }
        for (int i = 1; i < n; i++) {
    
            for (int j = 1; j < triangle.get(i).size(); j++) {
    
                dp[i][j] = Math.min(dp[i - 1][j], dp[i - 1][j - 1]) + triangle.get(i).get(j);
            }
        }
        int res = Integer.MAX_VALUE;
        for (int j = 0; j < triangle.get(n - 1).size(); j++) {
    
            res = Math.min(res, dp[n - 1][j]);
        }
        return res;
    }
}

The finger of the sword Offer II 098. Number of paths （ secondary ）

class Solution {
    
    public int uniquePaths(int m, int n) {
    
        int[][] dp = new int[m][n];
        Arrays.fill(dp[0], 1);
        for (int i = 0; i < m; i++) {
    
            dp[i][0] = 1;
        }
        for (int i = 1; i < m; i++) {
    
            for (int j = 1; j < n; j++) {
    
                dp[i][j] = dp[i - 1][j] + dp[i][j - 1] ;
            }
        }
        return dp[m - 1][n - 1];
    }
}

72. Edit distance ( difficult )

1、 Status and selection ： State means word1 and word2 The minimum editing distance of , As the comparison length changes , This state will change with it , Each state has 4 A choice ： unchanged , Delete , Replace and add .
For the sake of calculation , Double pointer traversal from back to front .
Insertion time ：

deleted ：

When replacing ：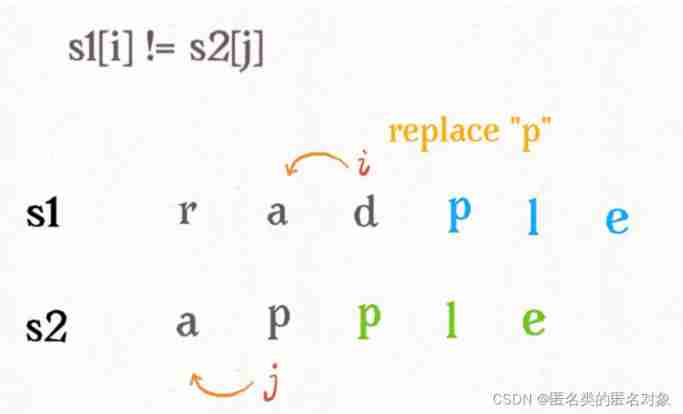

2、dp Array ： According to the State ,dp【i】【j】 On behalf of word1【0…i】 and word2【0…j】 The minimum editing distance of .
3、 State transition equation ： According to the choice ,dp【i】【j】=min{dp【i-1】【j】,dp【i-1】【j-1】,dp【i】【j-1】}+1 perhaps dp【i-1】【j-1】.
4、base case： Same as above ,dp【i】【j】 And the left , above , The upper left three directions are related . Simultaneous basis dp Definition of array ,dp【i】【0】=i,dp【0】【j】=j;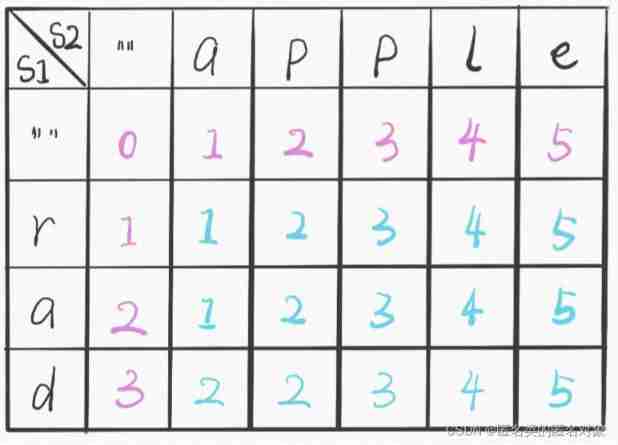

class Solution {
    
   public int minDistance(String word1, String word2) {
    
        int n = word1.length(), m = word2.length();
        //dp[i][j]：word1[0...i] and word2[0...j] The minimum editing distance of 
        int[][] dp = new int[n+1][m+1];
        //base case
        for (int i = 0; i <= n; i++) {
    
            dp[i][0] = i;
        }
        for (int j = 0; j <= m; j++) {
    
            dp[0][j] = j;
        }
        // State transition equation 
        for (int i = 1; i <= n; i++) {
    
            for (int j = 1; j <= m; j++) {
    
                if (word1.charAt(i - 1) == word2.charAt(j - 1)) {
    
                    dp[i][j] = dp[i - 1][j - 1];
                } else {
    
                    // Delete , Replace , increase 
                    dp[i][j] = 1 + Math.min(dp[i - 1][j], Math.min(dp[i][j - 1], dp[i - 1][j - 1]));
                }
            }
        }
        return dp[n][m];
    }
}

300. The longest increasing subsequence

Be careful 「 Subsequence 」 and 「 Substring 」 The difference between these two nouns , The substring must be continuous , And subsequences are not necessarily continuous .
1、 Be clear about status and choice ： The status is nums【i】 The longest increasing subsequence of . With the progress of Dynamic Planning ,i from 0 To n. Each state has two different choices for each subsequent number , Choose or not .
2、 Determine according to the status dp Array ： Determine according to the status ,dp【i】 It is defined as nums【i】 The length of the longest incrementing subsequence at the end .
3、 Determine the state transition equation according to the selection ： There are two options for each state ,dp【i】=max{dp【i】,dp【j】+1},（i∈【0,n】,j∈【0,i））.
4、 determine base case： according to dp Array definition and state transition equation , Just make sure dp【0】 You can determine each of the following dp 了 .

class Solution {
    
   int dp[];   //dp【i】 In order to num【i】 The length of the longest incrementing subsequence at the end 

    public int lengthOfLIS(int[] nums) {
    
        dp = new int[nums.length];
        Arrays.fill(dp, 1);
        for (int i = 0; i < nums.length; i++) {
    
            for (int j = 0; j < i; j++) {
    
                if (nums[i] > nums[j]) {
    
                    dp[i] = Math.max(dp[i], dp[j] + 1);
                }
            }
        }
        int max = Integer.MIN_VALUE;
        for (int i = 0; i < dp.length; i++) {
    
            if (dp[i] > max) {
    
                max = dp[i];
            }
        }
        return max;
    }
}

53. Maximum subarray and （ Simple ）

1、 Status and selection ： The state is the largest subarray and , There are two options for each state , Or add the following number , Or the latter number will form a school of its own .
2、dp To define an array ： Determine according to the status dp【i】 Stands for nums【i】 Is the largest subarray at the end and .
3、 State transition equation ：dp【i】=max{nums【i】,dp【i-1】+nums【i】},i∈【1,n】（ among ,nums【i】 It means no choice nums【i】, Its own school , The latter represents choice nums【i】）.
4、base case：dp【0】=nums【0】
5、 Optimize ： because dp【i】 Only with dp【i-1】 of , So you can be right dp Do state compression , The space complexity will be O（1）.

class Solution {
    
   public int maxSubArray(int[] nums) {
    
        int n = nums.length;
        //base case
        int dp_0 = nums[0];
        int dp_1 = 0, res = dp_0;
        // State transition equation 
        for (int i = 1; i < n; i++) {
    
            dp_1 = Math.max(nums[i], dp_0 + nums[i]);
            dp_0 = dp_1;
            res = Math.max(res, dp_1);
        }
        return res;
    }
}

1800. The largest ascending subarray and （ Simple ）

This question is the same as the question , Just dealing with dp【i】 You need to add judgment conditions , If nums【i】>nums【i-1】, Join in nums【i】, otherwise ,nums【i】 A school of its own , restart .

class Solution {
    
    public int maxAscendingSum(int[] nums) {
    
        int n = nums.length;
        //base case
        int dp_0 = nums[0];
        int dp_1 = 0, res = dp_0;
        // State transition equation 
        for (int i = 1; i < n; i++) {
    
            if (nums[i] > nums[i - 1]) {
    
                dp_1 = Math.max(nums[i], dp_0 + nums[i]);
            }else{
    
                dp_1=nums[i];
            }
            dp_0 = dp_1;
            res = Math.max(res, dp_1);
        }
        return res;
    }
}

Throwing eggs in high buildings

What's the problem 「 state 」, what are you having? 「 choice 」, Then exhaustive .

**「 state 」** Obviously , Is the current number of eggs K And the number of floors to be tested N. As the test goes on , The number of eggs may be reduced , The search scope of floors will be reduced , This is the change of state .

**「 choice 」** In fact, it is to choose which floor to throw eggs . Review the linear scanning and binary thinking just now , Each time you choose to throw eggs in the middle of the floor section , The linear scan chooses to test up one layer at a time . Different choices will cause the state to shift .

Now it's clear 「 state 」 and 「 choice 」, The basic idea of dynamic planning is formed ： It must be two-dimensional dp Array or with two state parameters dp Function to represent the state transition ; Plus one. for Loop through all the choices , Choose the best choice to update the results ：

651. Four key keyboard （ secondary ）

public int maxA(int N) {
    
        int[] dp = new int[N];//dp[i]=value On behalf of i There is value individual a
        dp[0] = 0;  //base case, Press down 0 Time of a The number is 0;
        for (int i = 1; i < N; i++) {
    
            // state 1： whole a
            dp[i] = dp[i - 1] + 1;
            //  state 2： It ends with ctrl+v： Future generations  &  Copy  dp[j-2], Paste continuously  i - j  Time , Plus what's already on the screen 1 Time 
            //  There are  dp[j - 2] * (i - j + 1)  individual  A
            for (int j = 2; j < i; j++) {
    
                dp[i] = Math.max(dp[i], dp[j - 2] * (i - j + 1));
            }
        }
        return dp[N];   // Return to press N The largest after the second a The number of 
    }

Stone game

What's the problem 「 state 」, what are you having? 「 choice 」, Then exhaustive .

**「 state 」** Obviously , Is the current number of eggs K And the number of floors to be tested N. As the test goes on , The number of eggs may be reduced , The search scope of floors will be reduced , This is the change of state .
from i To j The optimal solution of the selected stone , As the test goes on ,i Increase or remain unchanged ,j Reduce or remain unchanged

**「 choice 」** In fact, it is to choose which floor to throw eggs . Review the linear scanning and binary thinking just now , Each time you choose to throw eggs in the middle of the floor section , The linear scan chooses to test up one layer at a time . Different choices will cause the state to shift .
Choose left or right
Now it's clear 「 state 」 and 「 choice 」, The basic idea of dynamic planning is formed ： It must be two-dimensional dp Array or with two state parameters dp Function to represent the state transition ; Plus one. for Loop through all the choices , Choose the best choice to update the results ：

class Solution {
    
    public boolean stoneGame(int[] piles) {
    
        int n = piles.length;
        Pair[][] dp = new Pair[n][n];
        for (int i = 0; i < n; i++) {
    
            for (int j = 0; j < n; j++) {
    
                dp[i][j] = new Pair(0, 0);
            }
        }
        for (int i = 0; i < n; i++) {
    
            dp[i][i].first = piles[i];
            dp[i][i].second = 0;
        }

        for (int l = 2; l <= n; l++) {
    
            for (int i = 0; i <= n - l; i++) {
    
                int j = l + i - 1;
                int left = piles[i] + dp[i + 1][j].second;
                int right = piles[j] + dp[i][j - 1].second;
                if (left > right) {
    
                    dp[i][j].first = left;
                    dp[i][j].second = dp[i + 1][j].first;
                } else {
    
                    dp[i][j].first = right;
                    dp[i][j].second = dp[i][j - 1].first;
                }
            }
        }
        Pair res = dp[0][n - 1];
        return res.first - res.second;
    }
}

class Pair {
    
    int first;
    int second;

    public Pair(int first, int second) {
    
        this.first = first;
        this.second = second;
    }
}

summary

Tips ： Here is a summary of the article ：
for example ： That's what we're going to talk about today , This article only briefly introduces pandas Use , and pandas Provides a large number of functions and methods that enable us to process data quickly and conveniently .