Input of mathematical formula of obsidan

Preface ：

 Recently, I am studying advanced mathematics of upgraded college , Want to continue using Obsidian As a note taking software , But I don't know how to input mathematical formulas , Hence this article 

LaTex The grammar of

Be careful ： The mathematical formulas here should be in $ Here $, perhaps $$ Here $$

First, let's talk about how to change careers

$$
\begin{aligned}a=b+c\\b=c-a\\c=a+b \end{aligned}
$$

$$\begin{array}{r}a=b+c\\ b=c-a\\ c=a+b\end{array}$$

$$
\begin{matrix} It is known that y=\sqrt{x+3}&&(x>=0)\\ seek y What is the maximum value of  \end{matrix}
$$

$$\begin{array}{ccc}hasknowy=\sqrt{x+3}& & (x>=0)\\ seekyOfmostBigvalueyesmanyLess& & \end{array}$$

$$
\begin{bmatrix} It is known that y=\sqrt{x+3}&&(x>=0)\\ seek y What is the maximum value of  \end{bmatrix}
$$

$$\left[\begin{array}{ccc}hasknowy=\sqrt{x+3}& & (x>=0)\\ seekyOfmostBigvalueyesmanyLess& & \end{array}\right]$$

$$
\begin{Bmatrix} It is known that y=\sqrt{x+3}&&(x>=0)\\ seek y What is the maximum value of  \end{Bmatrix}
$$

$$\left\{\begin{array}{ccc}hasknowy=\sqrt{x+3}& & (x>=0)\\ seekyOfmostBigvalueyesmanyLess& & \end{array}\right\}$$

$$
 \begin{vmatrix}
 0&1&2\\
 3&4&5\\
 6&7&8\\
 \end{vmatrix}
 $$

$$\left|\begin{array}{ccc}0& 1& 2\\ 3& 4& 5\\ 6& 7& 8\end{array}\right|$$

$$
 \begin{Vmatrix}
 0&1&2\\
 3&4&5\\
 6&7&8\\
 \end{Vmatrix}
 $$

$$\Vert \begin{array}{ccc}0& 1& 2\\ 3& 4& 5\\ 6& 7& 8\end{array}\Vert$$

• The Greek letter

$\alpha$、$\beta$、$\chi$、$\Delta$、$\Gamma$、$\Theta$ And so on.

• Some mathematical structures

• The effect is as follows ：

$\frac{123}{999}$、$\sqrt[n]{abc}$、$\frac{\sqrt{234}}{\sqrt[n]{abc}}$、$\underrightarrow{abc}$、$\overrightarrow{abc}$

$\frac{123}{999}$、$\sqrt[n]{abc}$、$\frac{\sqrt{234}}{\sqrt[n]{abc}}$、$\underrightarrow{abc}$、$\overrightarrow{abc}$

• Insert delimiter

• The effect is as follows

$|$、$\|$、$\Uparrow$、$\{\}$

$|$、$\Vert$、$\Uparrow$、$\{\}$

• Insert some variable size symbols

The effect is as follows ：

$\sum$、$\int$、$\oint$、$\iint$、$\bigcap\bigcup\bigoplus\bigotimes$

$\sum$、$\int$、$\oint$、$\iint$、$\bigcap \bigcup ⨁⨂$

• Insert some function names

The effect is as follows ：

$\sin$、$\cos$、$\tan$、$\log$、 $\tan(at-n\pi)$

$\sin$、$\cos$、$\tan$、$\log$、 $\tan (at-n\pi )$

• Relational operators and binary operators

The effect is as follows ：

$\times$、$\ast$、$\div$、$\pm$、$\leq$、$\geq$、$\neq$、$\thickapprox$、$\sqsupset$、$\subset$、$\supseteq$、$\sqsupset$、$\sqsupseteq$、$\in$

$\times$、$\ast$、$÷$、$\pm$、$\le$、$\ge$、$\ne$、$\approx$、$⊐$、$\subset$、$\supseteq$、$⊐$、$⊒$、$\in$

• Insert arrow symbol

The effect is as follows ：

$\leftarrow$、$\Leftarrow$、$\nLeftarrow$、$\rightleftarrows$

$\leftarrow$、$\Leftarrow$、$\nLeftarrow$、$\rightleftarrows$

• Other symbols

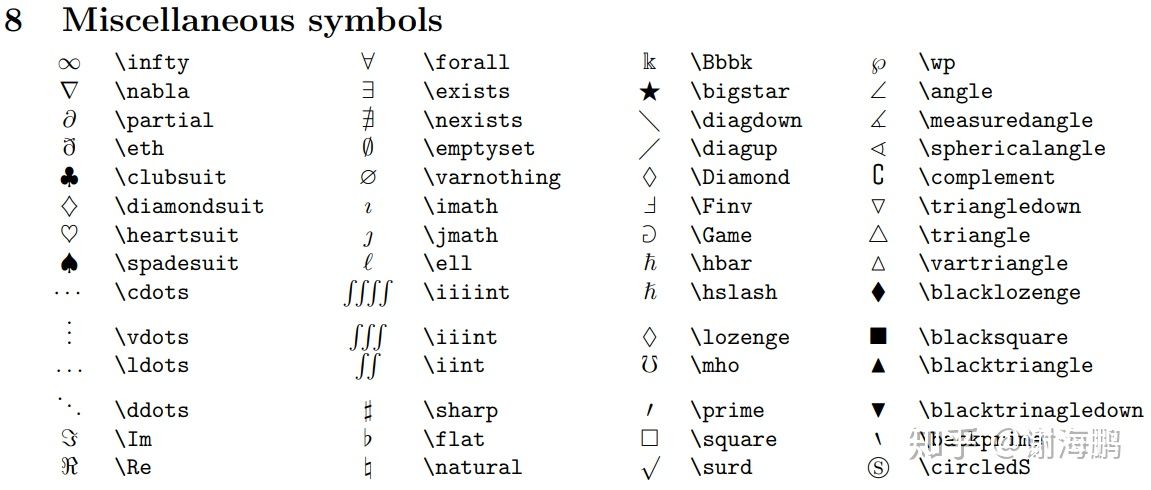
• The effect is as follows

$\infty$、$\angle$、$\int$、$\triangle$、$\square$

$\infty$、$\angle$、$\int$、$△$、$\square$

• Insert superscript and subscript

use ^ Means superscript , use _ Indicates the lower mark

The effect is as follows ：

$${\sin }^2(\theta )+{\cos }^2(\theta )=1$$
$$\sum _{n=1}^{\infty }k$$
$${\int }_a^{b}f(x)dx$$
$$\underset{x\to \infty }{\lim }\exp (-x)=0$$

• Be careful ：\, The function in the integral is to increase the distance ,\! Will reduce some spacing .

• Output piecewise function
  use \begin{cases} and \end{cases} To construct piecewise functions , In the middle \\ Let's break it up

$$f(x)=\{\begin{array}{l}2x,x>0\\ 3x,x\le 0\end{array}$$

• Some common mathematical formulas

 $$
 f'(x) = x^2 + x
 $$

$$f^{\prime }(x)=x^2+x$$

$$
 \lim_{x\to0}\frac{9x^5+7x^3}{x^2+6x^8}
$$

$$\underset{x\to 0}{\lim }\frac{9x^5+7x^3}{x^2+6x^8}$$

$$
 \int_a^b f(x)\,dx
 $$

$${\int }_a^{b}f(x)dx$$

$$
 \int_0^{+\infty}f(x)\,dx
$$

$${\int }_0^{+\infty }f(x)dx$$

$$
 \int_{x^2+y^2\leq R^2} \,f(x,y)\,dx\,dy = \int_{\theta=0}^{2\pi}\int_{r=0}^R \,f(r\cos\theta,r\sin\theta)\,r\,dr\,d\theta
 $$

$${\int }_{x^2+y^2\le R^2}f(x,y)dxdy={\int }_{\theta =0}^{2\pi }{\int }_{r=0}^{R}f(r\cos \theta ,r\sin \theta )rdrd\theta$$

$$
 \int\!\!\!\int_D f(x,y)dxdy
 $$

$$\int {\int }_{D}f(x,y)dxdy$$

Reference resources ：

https://zhuanlan.zhihu.com/p/158156773