A method to measure the similarity of time series: from Euclidean distance to DTW and its variants

author | Huang Chunxi

Company | Hong Kong University of science and technology

Research direction |  Intelligent Transportation

Abstract

According to the different characteristics of time series , Measurement of time series similarity （ Measurement of distance between time series ） There are many ways . This paper starts from Euclidean distance , Further extend to Dynamic Time Warping（DTW）、 some DTW Existing shortcomings and related solutions, as well as DTW Two variants of Derivative Dynamic Time Warping（DDTW） and Weighted Dynamic Time Warping（WDTW）.

Preface / background

In a wide range of scientific research fields , Time series is a ubiquitous data format . For time series related research , One of the most common requirements is to compare whether two time series are similar . Effectively comparing the similarity between time series is in many Sciences / It is very necessary and critical in engineering tasks , Such as ： classification / clustering / speech recognition / Gait recognition, etc .

Take a certain item of finished products in a manufacturing process （ some ） Take the time series data collected by the feature as an example . First , The collected time series data representing good products and defective products are different in some specific characteristics , And these differences have specific physical meanings related to domain knowledge ; secondly , Due to its own characteristics in the manufacturing process , The length of the collected time series data is not equal ; Again , There are many reasons for defective products , let me put it another way , Finished products can not only be divided into two categories: good products and defective products , It can be further divided into good products 、 Type of defective products 1、 Type of defective products 2、 Type of defective products 3 And so on ; Last , Like many data in actual production , The data volume of good products is much larger than that of defective products , The data of various categories of defective products that continue to be subdivided are even less , There is a serious data imbalance problem on the whole .

In order to realize the multi classification task of good products and different kinds of defective products in the normal production and manufacturing process , Comparing the similarity between the collected time series is an important step . Intuitively, it's not difficult to understand , Comparing the similarity of time series is equivalent to calculating the similarity between time series “ distance ”, Between two time series “ distance ” The bigger it is , The similarity between the two is smaller , On the contrary, the same is true .

Therefore, based on this, this paper starts from Euclidean distance , Further extend to Dynamic Time Warping（DTW）、 some DTW Shortcomings and related solutions as well DTW Two variants of Derivative Dynamic Time Warping（DDTW） and Weighted Dynamic Time Warping（WDTW）. In view of DTW The details of have been introduced in many high-quality blog posts , Therefore, this article only expounds the basic concepts 、 Pay more attention to the differences between different methods 、 The logic of transition and the problems applicable to different methods .

Euclidean distance

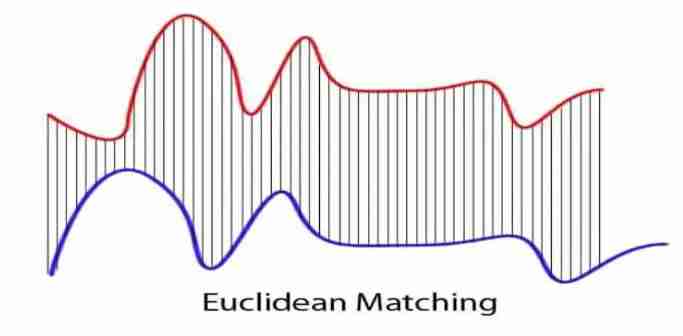
Mention measuring the distance between time series , Euclidean distance （Euclidean Distance） It's the most direct way , Its concept is simple , I won't go into details here . When Euclidean distance is applied to compare two time series , Each point between sequences establishes a one-to-one correspondence in sequence , According to the corresponding relationship between points, the Euclidean distance is calculated as the distance measure between two time series （ Similarity degree ）. Here's the picture 1 Shown ：

▲ chart 1. Euclidean distance between two equal length time series

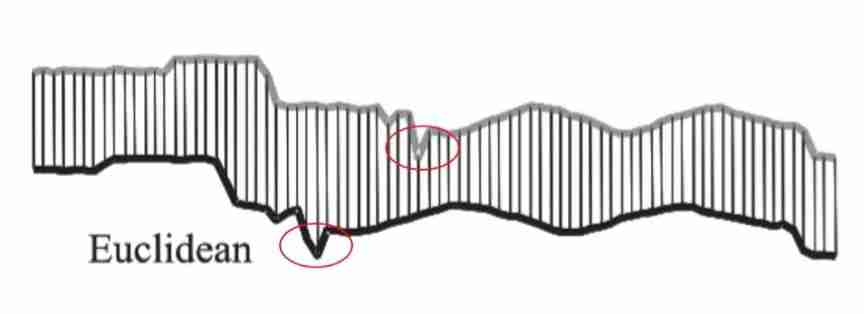
When applying Euclidean distance , The... In the first time series i The points are respectively related to the... In the second time series i Points form one-to-one correspondence . However , Euclidean distance can be problematic in some cases , Here's the picture 2 Shown ：

▲ chart 2. Whether the Euclidean distance between two unequal time series is feasible ？

When the length of two time series is not equal , A longer time series will always leave points that cannot be matched , How to calculate Euclidean distance in this case ？ without doubt , At this time, Euclidean distance is no longer feasible . Besides , Pictured 1 In the red circle , The two time series have some translation on the time axis, but the overall trend is similar , Naturally , When we want to artificially align graphs 1 In two time series , The two downward convex points in the red circle should correspond to each other . Obviously , This way of Euclidean distance, point-to-point method in order, can not meet our needs .

Sum up , In the distance measurement between time series , Euclidean distance has the following limitations ：（1） It is only suitable for processing equal length time series ;（2） Cannot consider when aligning time series  X  The change on the axis , Sometimes the alignment is unnatural .

Specially , As a common standard distance measure , Euclidean distance is another more extensive distance measure —— Min distance （Minkowski distance） When p The value is 2 The special case of time . Min distance p=1 Time and p=infinity when , Corresponding to Manhattan distance and the maximum value of the distance difference between two time series points .

DTW (Dynamic Time Warping)

For the Euclidean distance mentioned above, unequal length data cannot be processed 、 There are two main problems of unnatural alignment when dealing with equal length data , In order to solve the distance measurement and matching problem of unequal length data , In the last century 70 years , Japanese scholars Itakura And so forth DTW. In the last few decades ,DTW It has been widely used in isolated word speech recognition 、 Gesture recognition 、 Data mining and information retrieval ,DTW Once the mainstream method of speech recognition .DTW The principle of is briefly described here ：

For two time series of unequal length Q and C, The lengths are n and m：

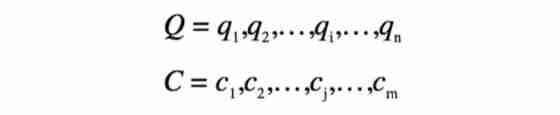
To use DTW To align two unequal time series , You need to build a n*m The distance matrix of , The... In the matrix i Xing di j The element corresponding to the column represents the midpoint of the sequence Sum point Distance of , Usually, Euclidean distance is used here , therefore . See the figure below 3：

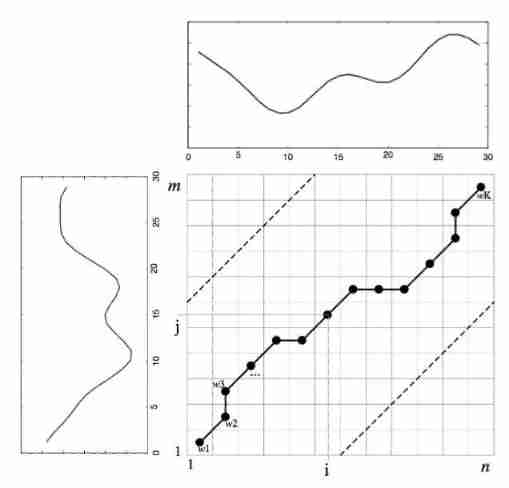
▲ chart 3. DTW Medium warping path Sketch Map

The figure above shows n*m Matrix , Each square represents each element in the matrix . For two time series ,DTW Throw away the restriction of Euclidean distance , Its original intention is to find a continuous matching relationship containing all points in two time series corresponding to each other （ This match can be the number Points correspond to A little bit ,）, Together, these sets of matching relationships form a graph 3 Black solid line in warping path W：

To carry out DTW matching ,warping path W The following conditions must be met ：

1- Borderline （Boundary conditions）： and , In short , Two classics DTW Aligned time series should be head to head 、 End to end , Reflected in the distance matrix is warping path Start from a corner 、 Stop at the other corner in the diagonal direction .

2- Continuity （Continuity）： Every time warping path The next move must be continuous , Reflected in the distance matrix is that the next step can only be selected from the adjacent squares of the original square （ The direction should meet the diagonal direction ）. Mathematically, it can be written as ： about ,, Need to meet , .

3- monotonicity （Monotonicity）： The correspondence between the two time series must be carried out in sequence ,warping path No cross . Mathematically, it can be written as ：,, Need to meet ,.

Those who meet these conditions W There are still many ,DTW Only seek to minimize warping cost Of W：

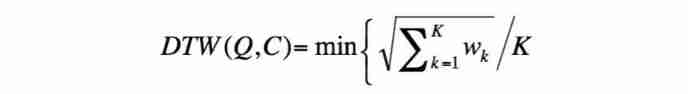
In the upper form ,K yes warping path The length of , Divide K Can eliminate different length warping path Influence .

Final , The corresponding relationship between two unequal length time series data can be obtained by solving the following recursive formula through dynamic programming ：

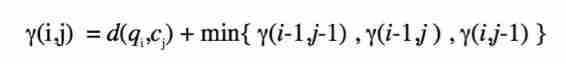
among , Is to the distance matrix Xing di Accumulated during the column warping path The total distance .

DTW Problems and solutions

Even though DTW It has been successfully applied in many fields ,DTW There are still shortcomings ： Sometimes DTW Unnatural distortion will occur during alignment / warping . Here's the picture 4 Shown ：

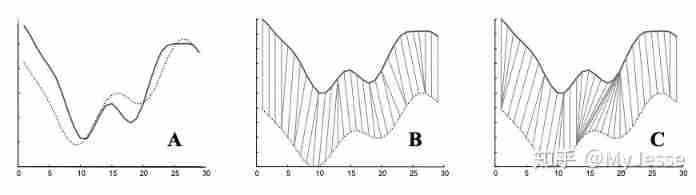
▲ chart 4. In synthetic data DTW Produced during alignment Singularities

A Medium solid line 、 The dotted line shows two synthetic signals （ mean value 、 The variance is the same ）,B What is shown in is natural “feature to feature” Corresponding , and C What is shown in is DTW Result . It's not hard to find out ,DTW The wave crest in the figure cannot be naturally corresponding to the wave crest , Instead, a point in one sequence corresponds to multiple points in another sequence , This situation is called “Singularities”. The reason for this is DTW The algorithm tries to twist X Axis to explain Y The change on the axis .

In order to solve “Singularities” problem , Past studies have put forward many schemes , It can be roughly classified into the following three categories ：

1-Windowing： in the final analysis , appear singularities It is because the points far away from each other in the two time series are only the same value / Close is easy to be warping together . Can restrict DTW stay warping In the process, we can choose the scope to solve singularities, You can set a warping window To achieve , So called Windowing Method . Mathematically writable ：, As window width Is a positive integer . chart 3 The range between the two dotted lines in the middle is the longitude window Limited scope , here warping path Only in this area .

2-Slope weighting： When tradition DTW When the recursive formula in is changed to the following formula , That is to say slope weighting.

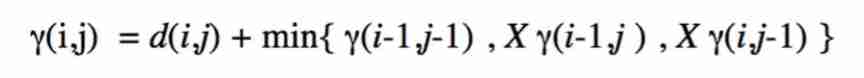
It's not hard to find out , The only difference is in min The last two terms in the function are preceded by X ,X Is a positive real number . When the X When adjusting the value of , You can make warping path The direction of （slope） There will be some adjustments .X When taking the larger value ,warping path Your choice will be more diagonal .

3-Step patterns： Change the tradition DTW The recursion in is the following formula, which can realize the change warping path step.

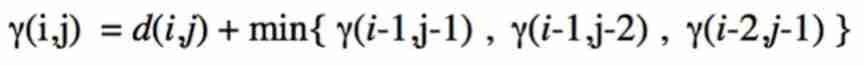
Will tradition DTW The recursion and the above formula in are visualized respectively as shown in the following figure 5 in A、B Shown ：

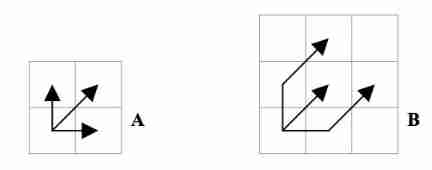
▲ chart 5. Two different step pattern Recursive visualization of

A The corresponding is tradition DTW The recursion of , The next step can only be selected from the three adjacent squares in the distance matrix , and B The corresponding in is change step Recursion after . Compare with A in ,B For each square that does not follow the diagonal direction in the first step, move one step towards the diagonal direction of the square where it is located , In this way, change can be achieved step pattern.

in general , To some extent, the above three kinds of solutions are helpful to solve singularities It helps , However , They still have the following shortcomings ：

（1） It is possible to miss the right warping path. The above three methods are artificial without any preconditions warping path Limit and adjust to reduce warpage , This is likely to miss the really right warping path.

（2） There is no clear guidance for the selection of parameters . stay Windowing In the method R Value selection 、Slope weighting In the method X They are all subjective adjustments based on specific scenes 、 There is no clear standard .

Derivative Dynamic Time Warping (DDTW)

actually ,DTW The reason for “Singularities”, Essentially due to DTW The characteristics considered by the algorithm itself determine ：DTW The algorithm only considers that the data points are Y The value on the axis .

for example ： Two data points and The value of is the same , however Located in the rising part of a time series , and Located in the downtrend part of a time series . about DTW for , It's easy to match these two points , Because their values are the same . However , Intuitively , It is difficult for us to match the two parts with opposite trends . for fear of DTW Only consider Y The value of the axis causes “Singularities” problem , DDTW There is .

DDTW Regardless of data points Y The value of the shaft , Instead, consider higher-level features —— Timing data “ shape ”. This method calculates the first derivative of time series data to obtain the relation with “ shape ” Relevant information , So it's called Derivative DTW.

DDTW The concept itself is also very simple , For tradition DTW for , The elements in the distance matrix are two points and Distance between ; However, for DDTW for , At this time “ Distance matrix ” The element in is no longer the distance between two points , It is the square of the difference of the first derivative of the time series data at two points . Although there are many ways to estimate the first derivative , For simplicity and expansibility ,DDTW The first derivative in is estimated by the following method ：

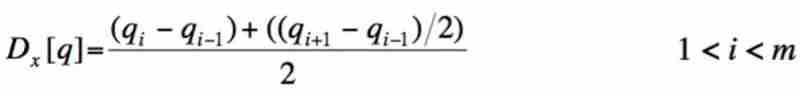
It's not hard to find out , stay The estimation of the first derivative at the point is the average of the slope of the straight line passing through the point and the left point of the point and the slope of the straight line passing through the left point and the right point of the point .Keogh, E. J., & Pazzani, M. J. mention , When only two data points are considered , This estimation method faces outliers More stable .

It should be noted that , This first derivative estimation method cannot calculate the first derivative of the first data point and the last data point of time series data , In practice, the derivative of the second data point and the penultimate data point can be used to replace . Besides , For high noise data sets, we can do it before estimating the first derivative exponential smoothing.

Weighted Dynamic Time Warping (WDTW)

Mentioned above , classical DTW The algorithm only considers Y The value on the axis , Without considering that the matching point is X The difference on the shaft , Therefore, it will cause the time series data matching “Singularities” problem .

in the final analysis ,“Singularities” The problem stems in part from considering only Y The value of the shaft , A point on the first sequence can be far away from another point on the second sequence （ here “ far ” refer to X Distance of axis / Ordinal number ） Points match , add DTW in warping path The continuity of 、 Monotonicity condition , It causes various warps in the process of timing data alignment / Distortion .

DDTW By considering “ shape ” This problem is solved by estimating the first derivative of time series data , and WDTW Different ideas are adopted . Simply speaking ,WDTW Choose to add one when calculating the Euclidean distance between two points on two sequences weight, And this weight And between two points X The distance on the axis is related . As follows （p=2）：

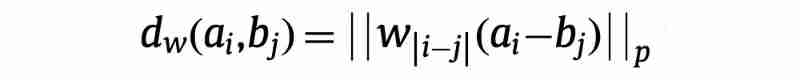
As above ,p=2 Time is to calculate two points on two sequences and Euclidean distance of . Here That is, with two points X The distance on the axis （phase difference） dependent weight.WDTW By calculating the Euclidean distance between two points, add a weight Methods , To solve the problem “Singularities” Problems provide new ideas ：weighted DTW It's essentially a penalized-based DTW, When It's worth more （ Two points are X The distance on the axis is large ） when , By giving a larger value , Then the algorithm can avoid matching two points with large distance .

in the light of WDTW,Jeong, Y. S., Jeong, M. K., & Omitaomu, O. A. Et al. Also proposed a logistic weight function To give weight , Interested readers can consult the original text by themselves . It is worth mentioning that , When When it's a constant , At this time WDTW Not for X The penalty for points with different distances on the axis is the same , So it is equivalent to the traditional DTW; When When the value of is maximum , At this time WDTW about X The penalty for points with different distances on the axis is also great , Even the i Point and number i-1 The matching of points is not good , At this time WDTW That is, corresponding to the traditional Euclidean distance .

Summary and supplement

Sum up , This paper starts from the Euclidean distance, which can only deal with equal length data and is easy to cause unnatural alignment , We discussed gradually DTW The reason and importance of the occurrence . further , We found that tradition DTW Algorithm brings singularities The problem can be in windowing、slope weighting、step pattern And other methods have been improved . However , Starting from the feature level considered by the algorithm , In order to solve DTW The algorithm may exist when matching time series data singularities problem ,DDTW Propose to consider higher-level features —— shape , And use the estimation of the first derivative to realize . Last ,WDTW It shows that it is a larger one that can contain Euclidean distance 、 Tradition DTW Distance measurement framework , meanwhile WDTW It also takes into account the phase difference To solve the problem singularities The question provides another way of thinking .

From the construction of distance matrix ,DTW And its variants have the same algorithm complexity , Are all . Besides , This article does not cover DTW Algorithm acceleration in large-scale dataset retrieval . actually , In large-scale applications , In the past, there have been many methods to correct DTW The algorithm accelerates , Such as ：FastDTW,LB_Keogh etc. .

reference

Keogh, E., & Ratanamahatana, C. A. (2005). Exact indexing of dynamic time warping.Knowledge and information systems,7(3), 358-386. 
Keogh, E. J., & Pazzani, M. J. (2001, April). Derivative dynamic time warping. InProceedings of the 2001 SIAM international conference on data mining(pp. 1-11). Society for Industrial and Applied Mathematics. 
Jeong, Y. S., Jeong, M. K., & Omitaomu, O. A. (2011). Weighted dynamic time warping for time series classification.Pattern recognition,44(9), 2231-2240.
Wikipedia .

Read more

# cast draft   through Avenue #

  Let your words be seen by more people  

How to make more high-quality content reach the reader group in a shorter path , How about reducing the cost of finding quality content for readers ？ The answer is ： People you don't know .

There are always people you don't know , Know what you want to know .PaperWeekly Maybe it could be a bridge , Push different backgrounds 、 Scholars and academic inspiration in different directions collide with each other , There are more possibilities . 

PaperWeekly Encourage university laboratories or individuals to , Share all kinds of quality content on our platform , It can be Interpretation of the latest paper , It can also be Analysis of academic hot spots 、 Scientific research experience or Competition experience explanation etc. . We have only one purpose , Let knowledge really flow .

  The basic requirements of the manuscript ：

• The article is really personal Original works , Not published in public channels , For example, articles published or to be published on other platforms , Please clearly mark  

• It is suggested that  markdown  Format writing , The pictures are sent as attachments , The picture should be clear , No copyright issues

• PaperWeekly Respect the right of authorship , And will be adopted for each original first manuscript , Provide Competitive remuneration in the industry , Specifically, according to the amount of reading and the quality of the article, the ladder system is used for settlement

  Contribution channel ：

• Send email ：[email protected] 

• Please note your immediate contact information （ WeChat ）, So that we can contact the author as soon as we choose the manuscript

• You can also directly add Xiaobian wechat （pwbot02） Quick contribution , remarks ： full name - contribute

△ Long press add PaperWeekly Small make up

Now? , stay 「 You know 」 We can also be found

Go to Zhihu home page and search 「PaperWeekly」

Click on 「 Focus on 」 Subscribe to our column

·