Information and entropy, all you want to know is here

️ This article references from [d2l] Information Theory
If this article helps you , Can pay attention to ️ + give the thumbs-up + Collection + Leaving a message. , Your support will be the biggest motivation for my creation

Besides , As mentioned in this article $\log (\cdot )$ Unless otherwise specified, it means ${\log }_2(\cdot )$.

One 、 Since the information （Self-information）

Let's start with an example . Roll a dice with even texture , There will be $6$ A possible result , And the probability of each result is $1/6$. Now? ：

• Set the event $X=\{\text{No more than}6\}$, Obviously $\mathbb{P}(X)=1$; Besides , This sentence is nonsense , It doesn't tell us anything , Because the number of points you get from rolling a dice will definitely not exceed $6$;
• Set the event $X=\{\text{No more than}5\}$, Obviously $\mathbb{P}(X)=5/6$; Besides , This sentence contains some information , But not much , Because we can almost guess the result ;
• Set the event $X=\{\text{The number of points is exactly equal to}2\}$, Obviously $\mathbb{P}(X)=1/6$; Besides , This sentence is more informative than the above sentence , because $\{\text{The number of points is exactly equal to}2\}$ Contains $\{\text{No more than}5\}$ Is in there .

As can be seen from this example , An event $X$ The amount of information contained is related to the probability of its occurrence . The smaller the probability, the greater the amount of information , The greater the probability, the less information .

Set the event $X$ The amount of information contained is $I(X)$, The probability of its occurrence is $p\triangleq \mathbb{P}(X)$, So how do we find $I(X)$ And $p$ The relationship between ？

First , We have the following common sense ：

• Observe a almost The amount of information obtained from certain events almost yes $0$;
• The amount of information obtained by observing two random variables together No more than The amount of information obtained by observing two random variables respectively and , And the inequality is equivalent and only if two random variables Are independent of each other .

Set the event $X=\{AAndBSame\; aswhenHairraw,ItsinA、Bphasemutualsinglestate\}$, Obviously $\mathbb{P}(X)=\mathbb{P}(A)\mathbb{P}(B)$, And according to the above common sense , And then there is $I(X)=I(A)+I(B)$. Might as well set $I(\ast )=f(\mathbb{P}(\ast ))$, be

$$f(\mathbb{P}(A)\cdot \mathbb{P}(B))=f(\mathbb{P}(X))=I(X)=I(A)+I(B)=f(\mathbb{P}(A))+f(\mathbb{P}(B))$$

It's not hard to see. $\log (\cdot )$ Can meet this requirement . But considering that $\log x$ stay $(0,1]$ Is non positive and monotonically increasing , So we usually use $-\log (\cdot )$ To measure the amount of information about an event .

Above all , set up event $X$ The probability of that happening is zero $p$, The amount of information （ also called Since the information ） It can be calculated in this way ：

$$I(X)=-\log p\text{\hspace{1em}(1)}$$

---

• When $(1)$ Type in the $\log$ With $2$ At the end of the day , The unit of self information is $\text{bit}$;
• When $(1)$ Type in the $\log$ With $e$ At the end of the day , The unit of self information is $\text{nat}$;
• When $(1)$ Type in the $\log$ With $10$ At the end of the day , The unit of self information is $\text{hart}$.

You can also get ：

$$1\text{nat}={\log }_{2}e\text{bit}\approx 1.443\text{bit},1\text{hart}={\log }_{2}10\text{bit}\approx 3.322\text{bit}$$

We know , For any length of $n$ The binary sequence of , It contains $n$ Bits of information . for example , For the sequence $0010$, The probability of its occurrence is $1/2^4$, therefore

$$I(\text{“0010”})=-\log \frac{1}{2^4}=4\text{bits}$$

Two 、 entropy （Entropy）

set up A random variable $X$ Obey the distribution $\mathcal{D}$, be $X$ The entropy of is defined as the expectation of its amount of information ：

$$H(X)={\mathbb{E}}_{X\sim \mathcal{D}}[I(X)]\text{\hspace{1em}(2)}$$

if $X$ It's a discrete distribution , be

$$H(X)=-{\mathbb{E}}_{X\sim \mathcal{D}}[\log p_i]=-\sum _i{p}_i\log p_i$$

if $X$ Is a continuous distribution , be

$$H(X)=-{\mathbb{E}}_{X\sim \mathcal{D}}[\log p(x)]=-\int p(x)\log p(x)\text{d}x$$

In the discrete case , set up $X$ Take only $k$ It's worth , Then there are ：$0\le H(X)\le \log k$.

Different from the amount of information , there $X$ It's a random variable, not an event
Take the event as a point , Then the amount of information can be regarded as the information generated by a point , And information entropy represents the average amount of information produced by a series of points
In the following chapters, we will only discuss discrete cases , Formulas in continuous cases can be analogized

2.1 Joint entropy （Joint Entropy）

We already know how to calculate $X$ Information entropy of , So how to calculate $(X,Y)$ Information entropy of ？

set up $(X,Y)\sim \mathcal{D}$, The joint probability distribution is $p_{ij}\triangleq \mathbb{P}(X=x_i,Y=y_j)$, Remember again $p_i=\mathbb{P}(X=x_i),p_j=\mathbb{P}(Y=y_j)$, According to the definition of information entropy, it is similar

$$H(X,Y)=-\sum _{ij}{p}_{ij}\log p_{ij}\text{\hspace{1em}(3)}$$

If $X=Y$, be $H(X,Y)=H(X)=H(Y)$; If $X$ and $Y$ Are independent of each other , be $p_{ij}=p_i\cdot p_j$, , in turn,

$$H(X,Y)=-\sum _{ij}(p_i\cdot p_j)(\log p_i+\log p_j)=-\sum _j{p}_j\sum _i{p}_i\log p_i-\sum _i{p}_i\sum _j{p}_j\log p_j=H(X)+H(Y)$$

Besides , The following inequality always holds ：

$$H(X),H(Y)\le H(X,Y)\le H(X)+H(Y)$$

2.2 Conditional entropy （Conditional Entropy）

Conditional entropy $H(Y|X)$ I have a random variable $X$ In the case of random variables $Y$ uncertainty , Defined as $X$ Given the conditions $Y$ The entropy pair of the conditional probability distribution $X$ Mathematical expectation ：

$$H(Y|X)=\sum _i{p}_{i}H(Y|X=x_i)=\sum _i{p}_i\left(-\sum _j{p}_{j|i}\log p_{j|i}\right)=-\sum _{ij}{p}_{ij}\log p_{j|i}\text{\hspace{1em}(4)}$$

utilize $p_{j|i}=p_{ij}/p_i$ Available

$$H(Y|X)=H(X,Y)-H(X)$$

It can be seen from the above formula ,$H(Y|X)$ Actually represents included in $Y$ But not included in $X$ Information in （ Be similar to $\mathbb{P}(B\backslash A)=\mathbb{P}(A\cup B)-\mathbb{P}(A)$）.

2.3 Mutual information （Mutual Information）

Given A random variable $(X,Y)$, We already know that $X$ Information can be used $H(X)$ To express ;$(X,Y)$ The total information can be used $H(X,Y)$ To express ; Included in $Y$ But not included in $X$ The information in can be used $H(Y|X)$ To express . Then what should we measure $X$ and $Y$ All contain information ？

The answer is Mutual information , Its definition is as follows （ It can be understood as a set $X$ And $Y$ Intersection ）：

$$I(X,Y)=H(X,Y)-H(Y|X)-H(X|Y)\text{\hspace{1em}(5)}$$

entropy 、 Joint entropy 、 Conditional entropy 、 The relationship between mutual information is as follows ：

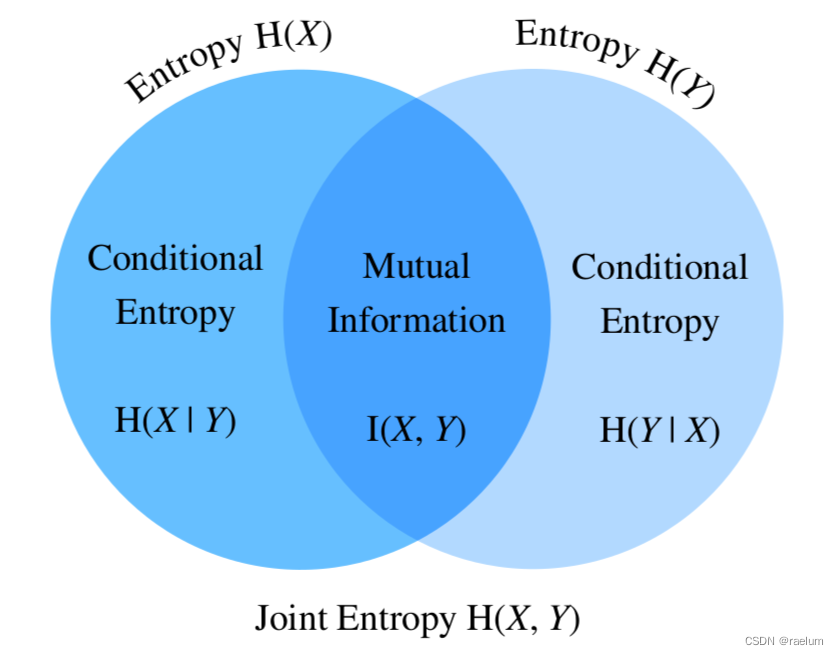
From the above figure, we can also get ：

$$\begin{array}{rl}I(X,Y)& =H(X)-H(X|Y)\\ I(X,Y)& =H(Y)-H(Y|X)\\ I(X,Y)& =H(X)+H(Y)-H(X,Y)\end{array}$$

We will $(5)$ Expand the equation to get

$$\begin{array}{rl}I(X,Y)& =-\sum _{ij}{p}_{ij}\log p_{ij}+\sum _{ij}{p}_{ij}\log p_{j|i}+\sum _{ij}{p}_{ij}\log p_{i|j}\\ & =\sum _{ij}{p}_{ij}(\log p_{j|i}+\log p_{i|j}-\log p_{ij})\\ & =\sum _{ij}{p}_{ij}\log \frac{p_{ij}}{p_i\cdot p_j}\\ & ={\mathbb{E}}_{(X,Y)\sim \mathcal{D}}\left[\log \frac{p_{ij}}{p_i\cdot p_j}\right]\end{array}$$

Some properties of mutual information ：

• symmetry ：$I(X,Y)=I(Y,X)$;
• Nonnegativity ：$I(X,Y)\ge 0$;
• $I(X,Y)=0$$\iff$$X$ And $Y$ Are independent of each other ;

2.4 Point mutual information （Pointwise Mutual Information）

Point mutual information is defined as ：

$$\text{PMI}(x_i,y_j)=\log \frac{p_{ij}}{p_i\cdot p_j}\text{\hspace{1em}(6)}$$

combination 2.3 section , We will find that the following relationship holds （ For example, information entropy is the expectation of information quantity , Mutual information is also the expectation of point mutual information ）

$$I(X,Y)={\mathbb{E}}_{(X,Y)\sim \mathcal{D}}\left[\text{PMI}(x_i,y_j)\right]$$

PMI The higher the value of , Express $x_i$ And $y_j$ The stronger the correlation .PMI Commonly used in NLP Calculate the correlation between two words in the task , But if the corpus is insufficient , There may be $p_{ij}=0$ The situation of , This leads to the mutual information of two words $-\infty$, Therefore, a correction is needed ：

$$\text{PPMI}(x_i,y_j)=\max (0,\text{PMI}(x_i,y_j))$$

Aforementioned PPMI Also known as On time mutual information （Positive PMI）.

3、 ... and 、 Relative entropy （KL The divergence ）

Relative entropy （Relative Entropy） Also known as KL The divergence （Kullback–Leibler divergence）, The latter is its more common name .

Set the random variable $X$ Obey probability distribution $P$, Now let's try another probability distribution $Q$ To estimate $P$（ hypothesis $Y\sim Q$）. remember $p_i=\mathbb{P}(X=x_i),q_i=\mathbb{P}(Y=x_i)$, be KL Divergence is defined as

$$D_{\text{KL}}(P\Vert Q)={\mathbb{E}}_{X\sim P}\left[\log \frac{p_i}{q_i}\right]=\sum _i{p}_i\log \frac{p_i}{q_i}\text{\hspace{1em}(7)}$$

KL Some properties of divergence ：

• Asymmetry ：$D_{\text{KL}}(P\Vert Q)\ne D_{\text{KL}}(Q\Vert P)$;
• Nonnegativity ：$D_{\text{KL}}(P\Vert Q)\ge 0$, The equation holds if and only if $P=Q$;
• If exist $x_i$ bring $p_i>0,q_i=0$, be $D_{\text{KL}}(P\Vert Q)=\infty$.

KL Divergence is used to measure the difference between two probability distributions . If the two distributions are exactly equal , be KL Divergence is $0$. therefore ,KL Divergence can be used as a loss function for multi classification tasks .

because KL Divergence does not satisfy symmetry , Therefore, it is not strictly “ distance ”

Four 、 Cross entropy （Cross-Entropy）

We will $(7)$ Type disassembly

$$D_{\text{KL}}(P\Vert Q)=\sum _i{p}_i\log p_i-\sum _i{p}_i\log q_i$$

If order $\text{CE}(P,Q)=-{\sum }_i{p}_i\log q_i$, Then the above formula can be written as

$$D_{\text{KL}}(P\Vert Q)=\text{CE}(P,Q)-H(P)$$

and $\text{CE}(P,Q)$ That's what we're talking about Cross entropy , It is formally defined as

$$\text{CE}(P,Q)=-{\mathbb{E}}_{X\sim P}[\log q_i]\text{\hspace{1em}(8)}$$

combination KL Nonnegativity of divergence , We can also get $\text{CE}(P,Q)\ge H(P)$, This inequality is also called Gibbs inequality .

Usually $\text{CE}(P,Q)$ It will also be written as $H(P,Q)$

---

An example of cross entropy calculation ：

$P$ It's a real distribution , and $Q$ Is the estimated distribution , Consider the three classification problem , For a sample , The actual labels and predicted results are listed in the following table ：

	Category 1	Category 2	Category 3
target	0	1	0
prediction	0.2	0.7	0.1

As can be seen from the table above , The real situation of this sample belongs to category 2, And $p_1=0,p_2=1,p_3=0,q_1=0.2,q_2=0.7,q_3=0.1$.

therefore

$$\text{CE}(P,Q)=-(0\cdot \log 0.2+1\cdot \log 0.7+0\cdot \log 0.1)=-\log 0.7\approx 0.5146$$

When a data set is given ,$H(P)$ It becomes a constant , therefore KL Both divergence and cross entropy can be used as the loss function of multi classification problems . When the real distribution $P$ yes One-Hot Vector time , Then there are $H(P)=0$, At this point, the cross entropy is equal to KL The divergence

4.1 Binary cross entropy （Binary Cross-Entropy）

Binary cross entropy （BCE） Is a special case of cross entropy

$$\begin{array}{rl}\text{BCE}(P,Q)& =-\sum _{i=1}^2{p}_i\log q_i\\ & =-(p_1\log q_1+p_2\log q_2)\\ & =-(p_1\log q_1+(1-p_1)\log (1-q_1))\end{array}$$

BCE It can be used as the loss function of two classification or multi label classification .

The loss of cross entropy is usually followed by Softmax, The binary cross entropy loss is usually followed by Sigmoid
Under the second category , The output layer can use a neuron +Sigmoid Two neurons can also be used +Softmax, The two are equivalent , But it's faster to train with the former

BCE Can also be through MLE obtain . Given $n$ Samples ：$x_1,x_2,\cdots ,x_n$, Label of each sample $y_i$ Not $0$ namely $1$（$1$ Representative positive class ,$0$ Representative negative class ）, The parameters of neural network are abbreviated as $\theta$. Our goal is to find the best $\theta$ bring ${\hat{y}}_i={\mathbb{P}}_{\theta }(y_i|x_i)$. set up $x_i$ The probability of being classified as a positive class is ${\pi }_i={\mathbb{P}}_{\theta }(y_i=1|x_i)$, Then the log likelihood function is

$$\begin{array}{rl}\ell (\theta )& =\log L(\theta )\\ & =\log \prod _{i=1}^n{\pi }_i^{y_i}(1-{\pi }_i{)}^{1-y_i}\\ & =\sum _{i=1}^n{y}_i\log {\pi }_i+(1-y_i)\log (1-{\pi }_i)\end{array}$$

Maximize $\ell (\theta )$ It's equivalent to minimizing $-\ell (\theta )$, The latter is the binary cross entropy loss .

---

Bloggers lack of talent and knowledge , If there are errors in this article, please point them out in the comment area