Fundamentals of digital circuit (V) arithmetic operation circuit

Fundamentals of digital circuits （ 5、 ... and ） Arithmetic Operation Circuits

One 、 Binary addition circuit

1. Half adder and full adder

（1） Half adder

A semi adder is one that only considers the addition of two one bit binary numbers , The arithmetic circuit without considering the low carry . The following figure shows the logic diagram of the half adder ：

$A$ and $B$ When the input of the terminal is different ,$S$ The sum of the output is 1; Phase at the same time ,S The output is 0, Conform to the addition rules of binary . But when $A$ and $B$ All for 1 when , A carry up will occur , here $C$ The output of is 1.

（2） Full adder

On the basis of half adder , Consider the carry of the local digit from the low order , Constitutes a full adder . According to the rules of binary addition , We first give the truth table of the full adder , As shown in the figure below ：

According to the truth table, we can write logical expressions ：
$$S_i=A_i\oplus B_i\oplus C_i,C_{i+1}=A_i{B}_i+C_i(A_I\oplus B_i)$$
Therefore, its logic diagram can be drawn as shown in the following figure ：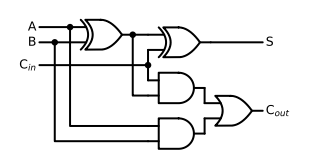

Full adder is the most basic arithmetic logic unit in computer .

2. adder

Only the traveling wave carry adder is introduced here , This kind of adder starts from the lowest bit to add , Gradually carry to the highest position , As the number of digits increases , Its computing speed will also slow down . When connecting the circuit , The number of adders is equal to the number of addends and the number of digits of addends , Although the calculation speed is not very fast , But its connection is relatively simple .
As shown in the figure is the connection diagram of a four bit traveling wave carry adder ：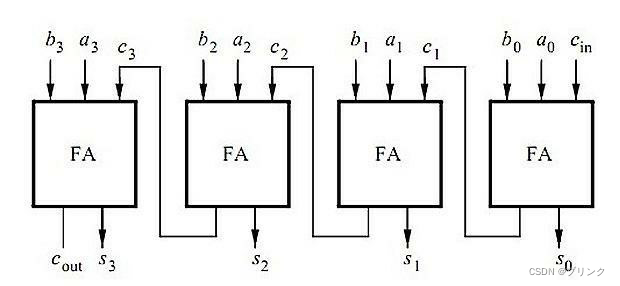

Two 、 Binary subtraction circuit

Although we can design half subtracter and full subtracter by logical expression of truth table , But we usually use adders to realize the function of subtraction .

1. Representation of binary positive and negative numbers

(1) Original code

The original code refers to adding a sign bit in front of the binary number , The sign bit of a positive number is 0, The sign bit of a negative number is 1, The rest of you represent the absolute value of numbers , such as ：+10110 The original code is 010110, and -10110 The original code is 110110.

(2) Complement code

The complement of a positive number is the same as itself .
The complement of a negative number is its own inverse plus 1, And its inverse code is obtained by inverting all digits except the sign bit . for example ：11101 The opposite of 10010, add 1 Get its complement, that is ：10011.

2. Subtraction circuits

Because subtracting a number is equal to adding a negative number , Minus a negative number is equal to plus a positive number , So we can use addition to realize subtraction . We have such a cycle in the clock ：
For example, the time is now 13:00, I want to arrive 12:00, Then there are two ways , One is to wait until 11 Hours ; One is time reversal 1 Hours ; Another example is now 20:00, I want to arrive 15:00, There are also two ways , The first is to wait 7 Hours （ The pointer now points to 3）, One is time reversal 5 Hours . We regard the waiting time as adding a number , Think of time reversal as subtracting a number , We found that , Add and subtract two different numbers , The results are the same , And we find that the sum of the absolute values of these two numbers is 12, Is a fixed value . Because the clock itself is a cycle , The principle of complement subtraction is the same , The complement and its own sum are always 0, Therefore, it is equivalent to subtracting a number and adding the complement of this number .
When we need to achieve this effect , Use the adder you learned before , Just convert the addend to the form of complement and add .