当前位置:网站首页>《统计学》第八版贾俊平第十章方差分析知识点总结及课后习题答案
《统计学》第八版贾俊平第十章方差分析知识点总结及课后习题答案
2022-07-06 09:23:00 【无二三事】
目录
一、知识框架
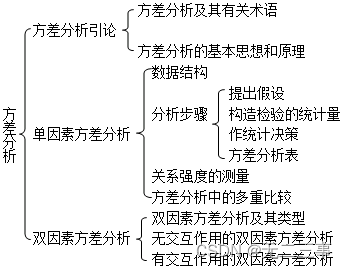
二、课后习题
1从3个总体中各抽取容量不同的样本数据,结果如表所示。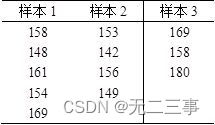
检验3个总体的均值之间是否有显著差异(α=0.01)。
解:设3个总体的均值分别为μ1,μ2,μ3。
提出假设:H0:μ1=μ2=μ3,H1:μ1,μ2,μ3不全相等。
由Excel输出的方差分析表,如表所示。

由于P-value=0.040877>α=0.01(或F=4.6574<F0.01(2,9)=8.0215),不拒绝原假设,没有证据表明3个总体的均值之间有显著差异。
2某家电制造公司准备购进一批5号电池,现有A,B,C三个电池生产企业愿意供货,为比较它们生产的电池质量,从每个企业各随机抽取5只电池,经试验得其寿命(单位:h)数据如表所示。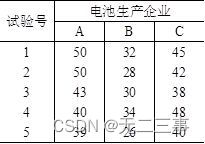
试分析三个企业生产的电池的平均寿命之间有无显著差异。(α=0.05)如果有差异,用LSD方法检验哪些企业之间有差异。
解:设3个企业生产的电池的平均寿命分别为μA,μB,μC。
提出假设:H0:μA=μB=μC;H1:μA,μB,μC不全相等。
由Excel输出的方差分析表,如表10-8、10-9所示。

表10-8

表10-9 方差分析表
由于P-value=0.0003<α=0.05(或F=17.0684>F0.05(2,12)=3.8853),拒绝原假设,表明电池的平均寿命之间有显著差异。
为判断哪两个企业生产的电池平均使用寿命之间有显著差异,首先提出如下假设:
检验1:H0:μA=μB;H1:μA≠μB。
检验2:H0:μA=μC;H1:μA≠μC。
检验3:H0:μB=μC;H1:μB≠μC。
计算检验统计量:
|xA-xB|=|44.4-30|=14.4
|xA-xC|=|44.4-42.6|=1.8
|xB-xC|=|30-42.6|=12.6
根据方差分析表10-9可知,MSE=18.03333。根据自由度=n-k=15-3=12,查t分布表得tα/2=t0.025=2.179。由于每个样本的样本量均为5,所以

由于|xA-xB|=14.4>LSD=5.85,拒绝原假设。因此,企业A与企业B电池的平均使用寿命之间有显著差异;
由于|xA-xC|=1.8<LSD=5.85,不拒绝原假设。因此,没有证据表明企业A与企业C电池的平均使用寿命之间有显著差异;
由于|xB-xC|=12.6>LSD=5.85,拒绝原假设。因此,企业B与企业C电池的平均使用寿命之间有显著差异。
3一家产品制造公司的管理者想比较A,B,C三种培训方式对产品组装时间是否有显著影响,将20名新员工随机分配给这三种培训方式。培训结束后,参加培训的员工组装一件产品所花的时间如表
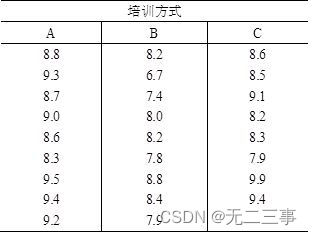
取显著性水平α=0.05。确定不同培训方式对产品组装的时间是否有显著影响?
解:设3种培训方式组装产品所花的平均时间分别为μA、μB、μC。
提出假设:H0:μA=μB=μC;H1:μA、μB、μC不全相等
由Excel输出的方差分析表,如表所示。

由于P-value=0.00196<α=0.05(或F=8.2745>F0.05(2,23)=3.4221),拒绝原假设。表明不同培训方式对产品组装有显著影响。
4某企业准备用三种方法组装一种新的产品,为确定哪种方法每小时生产的产品数量最多,随机抽取了30名工人,并指定每个人使用其中的一种方法。通过对每个工人生产的产品数进行方差分析得到下面的结果,如表所示。

要求:
(1)完成上面的方差分析表。
(2)若显著性水平α=0.05,检验采用三种方法组装的产品数量之间是否有显著差异。
解:(1)由Excel可得方差分析表中所缺的数值,如表所示。
(2)由方差分析表可知:P-value=0.245946>α=0.05(或F=1.478<F0.05(2,27)=3.554131),不能拒绝原假设,即没有证据表明3种方法组装的产品数量之间有显著差异。
5有5种不同品种的种子和4种不同的施肥方案,在20块同样面积的土地上,将5种种子和4种施肥方案搭配起来进行试验,取得的收获量数据如表所示。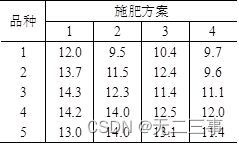
检验种子的不同品种对收获量的影响是否显著,不同的施肥方案对收获量的影响是否显著(α=0.05)。
解:设不同品种的种子的平均收获量分别为μ1,μ2,μ3,μ4,μ5。
提出假设:H0:μ1=μ2=μ3=μ4=μ5,H1:μ1,μ2,μ3,μ4,μ5不全相等
设不同施肥方式的平均收获量分别为μ1,μ2,μ3,μ4。
提出假设:H0:μ1=μ2=μ3=μ4,H1:μ1,μ2,μ3,μ4不全相等
由Excel输出的方差分析表如表所示。
由于P-value=0.0033<α=0.05(或F种子=7.2397>F0.05(4,12)=3.2592),拒绝原假设。表明不同品种的种子对收获量的影响有显著差异。
P-value=0.0019<α=0.05(或F施肥方案=9.2047>F0.05(3,12)=3.4903),拒绝原假设。表明不同施肥方案对收获量的影响有显著差异。
6为研究食品的包装方法和销售地区对其销售量是否有影响,在三个不同地区中用三种不同包装方法进行销售,获得的销售量数据如表所示。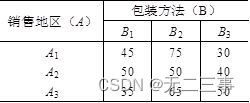
检验不同地区和不同包装方法对该食品的销售量是否有显著影响。(α=0.05)
解:设不同地区的平均销售量分别为μA1,μA2,μA3。
提出假设:H0:μA1=μA2=μA3,H1:μA1,μA2,μA3不全相等。
设不同包装的平均销售量分别为μB1,μB2,μB3。
提出假设:H0:μB1=μB2=μB3,H1:μB1,μB2,μB3不全相等。
由Excel输出的方差分析表如表所示。
由于P-value=0.9311>α=0.05(或F地区=0.0727<F0.05(2,4)=6.9443),不拒绝原假设。没有证据表明不同的地区对该食品的销售量有显著影响。
P-value=0.1522>α=0.05(或F包装方法=3.1273<F0.05(2,4)=6.9443),不拒绝原假设。没有证据表明不同的包装方法对该食品的销售量有显著影响。
7一家超市连锁店进行一项研究,确定超市所在的位置和竞争者的数量对销售额是否有显著影响。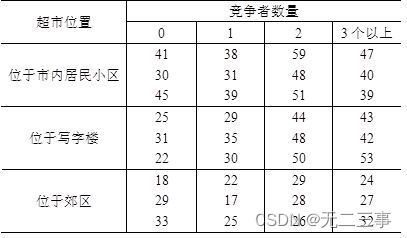
取显著性水平α=0.01,检验:
(1)竞争者的数量对销售额是否有显著影响。
(2)超市的位置对销售额是否有显著影响。
(3)竞争者的数量和超市的位置对销售额是否有交互影响。
解:由Excel输出的方差分析表如表所示。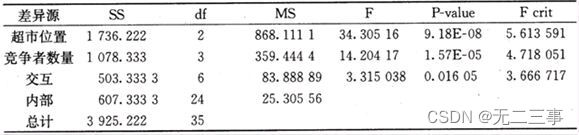
(1)提出假设:
H0:竞争者数量对销售额没有显著影响
H1:竞争者数量对销售额有显著影响
由于P-value=1.57E-5<α=0.01(或F竞争者数量=14.2042>F0.01(3,24)=4.7181),拒绝原假设。表明竞争者的数量对销售额有显著影响。
(2)提出假设:
H0:超市的位置对销售额没有显著影响
H1:超市的位置对销售额有显著影响
P-value=9.18E-08<α=0.01(或F超市位置=34.3052>F0.01(2,24)=5.6136),拒绝原假设。表明超市的位置对销售额有显著影响。
(3)提出假设:
H0:竞争者的数量和超市的位置对销售额没有交互影响
H1:竞争者的数量和超市的位置对销售额有交互影响
P-value=0.01605>α=0.01(或F交互作用=3.3150<F0.01(6,24)=3.6667),不拒绝原假设。没有证据表明竞争者的数量和超市的位置对销售额有交互影响。
边栏推荐
- SystemVerilog discusses loop loop structure and built-in loop variable I
- Spot gold prices rose amid volatility, and the rise in U.S. prices is likely to become the key to the future
- HackMyvm靶机系列(7)-Tron
- 7-11 mechanic mustadio (PTA program design)
- xray與burp聯動 挖掘
- Harmonyos JS demo application development
- [data processing of numpy and pytoch]
- 攻防世界MISC练习区(SimpleRAR、base64stego、功夫再高也怕菜刀)
- Nuxtjs quick start (nuxt2)
- 网络基础之路由详解
猜你喜欢
Chain team implementation (C language)

1143_ SiCp learning notes_ Tree recursion
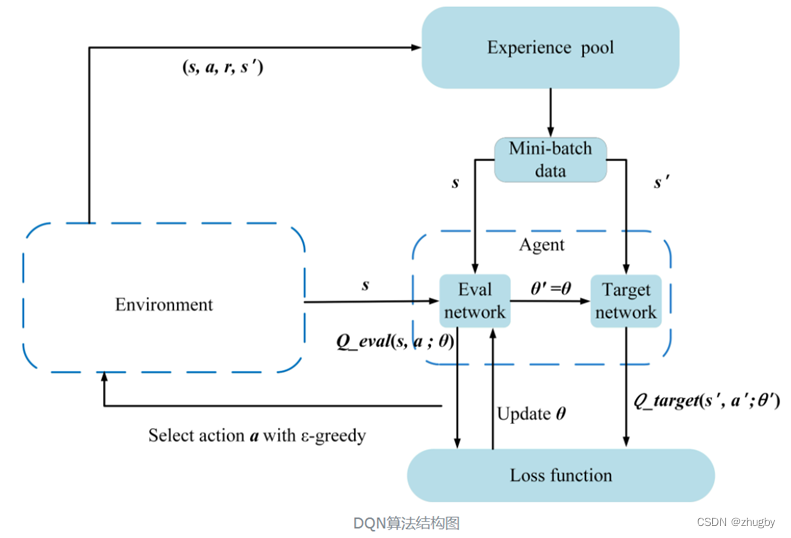
Intensive literature reading series (I): Courier routing and assignment for food delivery service using reinforcement learning

Meituan dynamic thread pool practice ideas, open source

Package bedding of components

SystemVerilog discusses loop loop structure and built-in loop variable I
内网渗透之内网信息收集(二)

链队实现(C语言)
Hackmyvm target series (4) -vulny

Intel oneapi - opening a new era of heterogeneity
随机推荐
JS several ways to judge whether an object is an array
记一次api接口SQL注入实战
The difference between layer 3 switch and router
强化学习基础记录
Simply understand the promise of ES6
On the idea of vulnerability discovery
记一次,修改密码逻辑漏洞实战
Intranet information collection of Intranet penetration (4)
Chain team implementation (C language)
msf生成payload大全
链队实现(C语言)
[VMware abnormal problems] problem analysis & Solutions
Canvas foundation 1 - draw a straight line (easy to understand)
7-9 make house number 3.0 (PTA program design)
Sword finger offer 23 - print binary tree from top to bottom
Hackmyvm target series (2) -warrior
Apache APIs IX has the risk of rewriting the x-real-ip header (cve-2022-24112)
网络基础详解
7-7 7003 combination lock (PTA program design)
JDBC read this article is enough