当前位置:网站首页>Mathematical modeling idea of 2022 central China Cup
Mathematical modeling idea of 2022 central China Cup
2022-07-06 14:15:00 【A little monk who loves learning】
B Question ideas
The whole question is relatively simple without portfolio investment , It gives macro data , First of all, macro data need to be predicted , Then select the index with high correlation to predict the stock trend , Whether linear regression or other algorithms can , The data can be supplemented by interpolation fitting , Subject to the stock time . Conformal spline interpolation is recommended for interpolation fitting , stay matlab Use filliming Functional pchip Parameter realization . Many people say that the time scales of indicators are different , One is based on the stock time , Other indicators are divided into each 5 Minute data , Or take the average by day , Anyway , Need to unify the time scale
K How to draw the line diagram is through Kplot Function implementation , There must be a picture in this paper , Generally, the prediction of stocks is based on the closing price .
Let's take a look at the first question , As I just said, we usually use the closing price of the stock to predict , So the main indicators here , It must be an indicator with high correlation with the closing price , The first question is relatively simple , Directly through the correlation method ( Cosine similarity is recommended 、 variance analysis ) Just do it , Not the principal component , That's the mapping basis vector , It is used to reflect the overall characteristics of data , Although it is the main ingredient , But this problem requires finding and “ Digital economy ” Important indicators related to plate , Don't use the wrong algorithm , The latter question also mentioned the trading volume , Here is a correlation analysis of trading volume , Find out the indicators with strong correlation .
The second question and the third question are to use the main indicators as input , The trading volume and closing price are used as output respectively , Bring in machine learning algorithms ( Recommend neural networks 、Xgboost) Medium training , Finally, remember to do error verification .
Fourth, ask here to popularize , You can buy more or empty , Buying more is when the stock goes up , You make money by buying , To buy short is to buy stocks lower and you earn , One is to buy, the other is to buy short , Don't go around , Be sure to record in the program , About how much to trade , We need to build a risk control model , The stock price assumes that the closing price is the price of a sum , Buy and sell later , All transactions are in whole numbers , Although the title is 2022 year 1 month 4 solstice 2022 year 1 month 28 The data of , If you refer to it, you must have a high income , Understand the background of the topic , It must be that you don't know the future data , The result of prediction , That is the result of the third question , And then on this basis , Take the prediction data segments in turn, for example k+1:k+n Of n Data analysis to see whether to buy or sell , If you buy, buy more or buy short , Similarly, take the real data segments in turn , If a loss is expected, the risk control mechanism will be triggered , Will clear the stock , Of course, you can also set different thresholds , The emptying ratio is different at different thresholds , For example, when it comes to value at risk 0.5 了 , Empty a part , To value at risk 0.8 了 , Clear all , And you spent your money on stocks , The value of stocks is not your cash , After selling, the money in hand can be used for reinvestment , Let's talk about the pullback rate again , you are here 1 A deal was made on the th , stay 2 A deal was made on the th , This is separate , If 1 A daily purchase that triggers the risk control mechanism to sell in case of risk is regarded as a withdrawal ,2 What I bought on the day just met the selling conditions and sold , So the pullback rate at this time is 50%, If it triggers your selling mechanism , Then it's not a retreat , This needs to be understood . The fourth question is not a simple prediction of buying and selling , There must be a need to restore the real stock trading scene , Risk control 、 purchase 、 Selling mechanisms need to build models , How to control risk , Take the real fragment data, for example k+1:k+n Of n Data for risk assessment , The simplest is to calculate the variance , How to buy , It is predicted that it will rise for some time , Take the prediction segment data. If it rises more times , Then you can buy , Also take the prediction segment data , If you drop more times, sell , This is the case of buying too much , So buying short is the same thing , General stock operating software will also set the selling line , For example, a rise 15% Automatic closing , falling 15% Automatic closing .
I don't suggest that you think the fourth question is too complicated , Can be appropriately simplified , The first thing to note is that the real data used for risk control and selling , Buying is based on forecast data , The second thing to pay attention to is to distinguish between buying more and buying short .
【 Detailed ideas ,C Updated 】
C The question is very simple , Needless to say, there are too many data , The data are interpreted accordingly , But note that the title doesn't give you what the data of the defect is , After you build the model, you need to set the threshold to judge , The title also talks about the waveform of the fifth middle school
If you can't read data, use matlab Import function
1) File format :
1 Signal voltage ,2 Signal voltage ,3 Signal voltage ,4 Signal voltage ,5 Signal voltage ,6 Signal voltage , Direction , pulse , Time stamp
1.61, 1.06, 0.97, 0.95, 0.98, 1.47, 1, 1, 102070423
2) There are six voltage values , The data of six steel ropes correspond to . A row of data is a frame of data . The first column represents the voltage value of the first rope , The second column represents the voltage value of the second rope ,…, The sixth column represents the voltage value of the sixth rope .
3) Direction “0” On behalf of , Direction “1” Indicates the uplink .
4) pulse : It's actually distance , Obtained by distance sensor . from 1 To n Increasing , Each frame ( A row of data represents a frame of data ) Corresponding to a pulse number , Every time the number of pulses increases 1, Represents an increase in distance 0.4 rice .
There may be multiple frames of data corresponding to one pulse ( It means that 0.4 Several measurements have been made within meters ). When drawing the waveform , The distance corresponding to each frame is equal to 0.4 Meters divided by frames .
5) Timestamp is mainly used to name files , Avoid repetition . This data can be ignored .
6) The length of steel wire rope is 960 rice , The position of the broken wire can be expressed in frames .
7) Each file records the monitoring data of one operation ,10 There are... Records 10 Monitoring data of round trip operation . Note that the uplink and downlink monitoring data are not recorded from the same end .
First question , Since the title says there is noise , Then wavelet denoising is OK , Then perform anomaly test , Note that the anomaly test here does not mean to use LOF The algorithm brings in all abnormal data to test , Instead, the fragments are checked by traversing the fragment data in turn according to the timestamp , The length of the data taken is self-determined , The simplest anomaly detection can be the percentage of the absolute value and the average value of the difference between the voltage value and the average value in the segment data according to the topic , Set the threshold to identify the corresponding abnormal points , Note that a voltage corresponds to a steel wire , pulse 1 The corresponding is 0.4 rice .
Wavelet denoising to a case program , Modify yourself
%% Initializer
clear,clc
t1=clock;
%% Load noise signal data , The data is .mat Format , And put it in the same folder as the program
load('filename.mat');%matrix
YSJ= filename;
%% Data preprocessing , The data may be stored in a matrix or EXCEL Two dimensional data in , Join into one-dimensional , If the data is one-dimensional data , This step also does not affect the data
[c,l]=size(YSJ);
Y=[];
for i=1:c
Y=[Y,YSJ(i,:)];
end
[c1,l1]=size(Y);
X=[1:l1];
%% Draw noise signal image
figure(1);
plot(X,Y);
xlabel(' Abscissa ');
ylabel(' Ordinate ');
title(' The original signal ');
%% Hard threshold processing
lev=3;
xd=wden(Y,'heursure','h','one',lev,'db4');% Signal sequence after hard threshold denoising
figure(2)
plot(X,xd)
xlabel(' Abscissa ');
ylabel(' Ordinate ');
title(' Hard threshold denoising ')
set(gcf,'Color',[1 1 1])
%% Soft threshold processing
lev=3;
xs=wden(Y,'heursure','s','one',lev,'db4');% The signal sequence after soft threshold denoising
figure(3)
plot(X,xs)
xlabel(' Abscissa ');
ylabel(' Ordinate ');
title(' Soft threshold denoising ')
set(gcf,'Color',[1 1 1])
%% Denoising after fixed threshold
lev=3;
xz=wden(Y,'sqtwolog','s','sln',lev,'db4');% Signal sequence after fixed threshold denoising
figure(4)
plot(X,xz);
xlabel(' Abscissa ');
ylabel(' Ordinate ');
title(' Denoising after fixed threshold ')
set(gcf,'Color',[1 1 1])
%% Calculate SNR SNR
Psig=sum(Y*Y')/l1;
Pnoi1=sum((Y-xd)*(Y-xd)')/l1;
Pnoi2=sum((Y-xs)*(Y-xs)')/l1;
Pnoi3=sum((Y-xz)*(Y-xz)')/l1;
SNR1=10*log10(Psig/Pnoi1);
SNR2=10*log10(Psig/Pnoi2);
SNR3=10*log10(Psig/Pnoi3);
%% Calculate the root mean square error RMSE
RMSE1=sqrt(Pnoi1);
RMSE2=sqrt(Pnoi2);
RMSE3=sqrt(Pnoi3);
%% Output results
disp('------------- Noise reduction results of three threshold setting methods ---------------');
disp([' Hard threshold denoising SNR=',num2str(SNR1),',RMSE=',num2str(RMSE1)]);
disp([' Soft threshold denoising SNR=',num2str(SNR2),',RMSE=',num2str(RMSE2)]);
disp([' Denoising after fixed threshold SNR=',num2str(SNR3),',RMSE=',num2str(RMSE3)]);
t2=clock;
tim=etime(t2,t1);
disp(['------------------ Running time ',num2str(tim),' second -------------------'])
Second questions , We need to dig out some indicators , Then evaluate through the evaluation algorithm , The resulting values are relative , Take it as the level of safety performance , The indicator can be the number of abnormal signals 、 Variance, etc , We can dig out as many indicators as possible .
【 Detailed ideas ,A Updated 】
An order contains multiple items , Each item has a different quantity , The title doesn't say the demand time of the order , Then consider how to finish sorting in the shortest time
In the Title Introduction, we can know , One shelf holds one kind of goods
Here are the problems we need to solve
In fact, as long as you understand the background first , It's very simple , Let's go straight to the first question, how to program
The first question is to divide the order of the day into multiple batches . It is required that the number of goods included in the order of each batch shall not exceed N=200 , And the fewer batches, the better ( The less the corresponding transfer times , The more efficient ). That is to say, the attachment 1 Package the order in , This is not a cluster , Don't mess about , Anyway, one batch will be put 200 A variety of goods , There is no talk about how much a shelf can hold , Then we don't care , How do we program , First 923 Order per order , Is my , I'll just use randperm Function to a random sequence , Then each one returns the index , Traverse in turn, save with matrix and pass unique Function de duplication , Until the type of goods does not exceed 200 As the first batch , Later on , Of course , It must be solved by optimization algorithm , This means that each of us is randperm Random sequence generated by function , Then the objective function is through the number of batches after packaging the order in turn , Let's go straight to the program
clear
clc
% Data preparation
N=200;
[~,~,X]=xlsread(' The attachment 1: Order information .csv');
X=string(X);
X(1,:)=[];
Y=unique(X(:,1));
n=length(Y);
Z=[];
V=[];
for i=1:size(Y)
z=X(find(X(:,1)==Y(i)),2);
Z{i,1}=z;% Record the number of goods under each order
V(i,1)=sum(double(X(find(X(:,1)==Y(i)),3)));
end
% Optimization , I'm just an early generation individual here , Write it yourself later
num=100;
x=[];
f=[];
for i=1:num
x(i,:)=randperm(n);
% Calculate the objective function
U=[];
UU=[];
u=1;
for j=1:n
UU=[UU;Z{x(i,j),1}];
UU=unique(UU);
if length(UU)<=N% If it is less than 200, Then record it directly
U{u,1}=UU;
else% If it is greater than , Then record it in the next batch
u=u+1;
UU=[];
UU=[UU;Z{x(i,j),1}];
U{u,1}=UU;
end
end
f(i,1)=u;% Record the maximum batch , Objective function
end
% Record the best
[bestf,b]=min(f);
bestx=x(b,:);
% Calculate the number of goods and the number of goods in each batch under the optimal scheme
F=[];% The first column is the number of goods in each batch , The second column is the number of goods
UU=[];
u=1;
f1=0;
f2=0;
for j=1:n
UU=[UU;Z{bestx(j),1}];
UU=unique(UU);
if length(UU)<=N% If it is less than 200, Then record it directly
f1=length(UU);
f2=f2+V(bestx(j),1);
F(u,:)=[f1,f2];
else% If it is greater than , Then record it in the next batch
u=u+1;
f1=0;
f2=0;
UU=[];
UU=[UU;Z{bestx(j),1}];
f1=length(UU);
f2=f2+V(bestx(j),1);
F(u,:)=[f1,f2];
end
end
Just add iteration later , Choose the best , The Monte Carlo simulation will not be done directly , The above program can directly apply a set of simulated annealing algorithm , Some partners are keen on genetic algorithm , Here is the crossover and mutation program I modified before , Share with you
function x=jiaocha(x,a,k_gen,num_gen)
% Crossover rate change
a = a*exp(-k_gen/num_gen);
for i = 1:size(x,1)
if rand < a
% Select the crossover site
b = randi(size(x,2))-1;
x(i,:)=[x(i,b+1:end),x(i,1:b)];
end
end
function x=bianyi(x,a,k_gen,num_gen)
% Rate of variation
a = a*exp(-k_gen/num_gen);
for i = 1:size(x,1)
if rand < a
% Select the mutation site
b1 = randi(size(x,2));
b2 = randi(size(x,2));
% Produce variation ( For sequence problems , Produce two variation points and exchange them )
c = x(i,b1);
x(i,b1)=x(i,b2);
x(i,b2)=c;
end
end
Apply other optimization algorithms can , The complete program will be released later
Second questions , On the basis of the first question , Consider Shelf Number , After packing a batch of orders, we can find the optimal placement , You know, there are many kinds of goods in an order , One item may be included in multiple orders , It is to see whether the goods of a batch are placed in a centralized way according to the current order , Picking distance has been given
The second question is to add an objective function , Then carry out multi-objective optimization , Non dominated sorting algorithm program to share with you
function [TT,chrom]=ns2(NN,F1,F2)
% Fast non dominated sorting
a = 0;
T1 = [];
T2 = [];
chrom=NN;
chrom1 = [];
chrom2 = [];
while a == 0 % Rank and sort according to the number of dominated
M = [];
for i = 1:length(F1)
M(i,1) = length(find(F1>F1(i,1)))+length(find(F2<F2(i,1)));% The objective function is minimized here as <, Maximize to >
end
b1 = [];
b2 = [];
[b1,b2] = sort(M); %b1 Returns the order from small to large ,b2 Returns the original sequence number
if length(chrom)>0 && b1(1) == 0 % The non dominated number enters the first level with T1 Matrix save
T1 = [T1;F1(b2(1)),F2(b2(1))];
chrom1 = [chrom1;chrom(b2(1),:)];
F1(b2(1)) = [];
F2(b2(1)) = [];
chrom(b2(1),:) = [];
else % There are dominated numbers to enter the second level T2 Matrix save
a = 1;
T2 = [F1,F2];
chrom2 = chrom;
end
end
T2 = T2(b2,:);
chrom2 = chrom2(b2,:);
if size(T1,1) > 2 %T1 The matrix does not need to be sorted by congestion adjustment , Direct pair T2 Just sort and adjust
y = yongji(T1);% Crowding degree
for i = 2:size(T1,1)
if y(i-1) > y(i)
T1(i-1:1:i,:) = T1(i:-1:i-1,:); % Adjust the ranking according to the congestion degree , If the latter is better than the former, reverse the order
chrom1(i-1:1:i,:) = chrom1(i:-1:i-1,:);
end
end
end
if length(T2) > 0 %T1 The matrix does not need to be sorted by congestion adjustment , Direct pair T2 Just sort and adjust
y = yongji(T2);% Crowding degree
for i = 2:size(T2,1)
if b1(i) == b1(i-1)
if y(i-1) > y(i)
T2(i-1:1:i,:) = T2(i:-1:i-1,:); % Adjust the ranking according to the congestion degree , If the latter is better than the former, reverse the order
chrom2(i-1:1:i,:) = chrom2(i:-1:i-1,:);
end
end
end
end
% Sort and reorganize
TT = [T1;T2];
chrom = [chrom1;chrom2];
function y=yongji(H)
% Calculate congestion
y1=H(:,1);
y2=H(:,2);
[yy1,a1]=sort(y1);
[yy2,a2]=sort(y2);
L=[];
L=[1 1];
for i=2:length(yy1)-1
L=[L;(yy1(i+1,1)-yy1(i-1,1))/(max(yy1)-min(yy1)),(yy2(i+1,1)-yy2(i-1,1))/(max(yy2)-min(yy2))];
end
L=[L;1 1];
L=[L(a1,1),L(a2,2)];
y=sum(L,2);
end
Third questions , On the basis of the second question , Consider multiple technicians , Third, programming is a little more complicated , Start by writing down the rules one by one , Be careful not to make a mistake , This question only selects one batch to study , You can also make several batches , Explain the stability of the model .
————————————————
边栏推荐
- HackMyvm靶机系列(4)-vulny
- 附加简化版示例数据库到SqlServer数据库实例中
- 实验九 输入输出流(节选)
- 7-4 hash table search (PTA program design)
- . Net6: develop modern 3D industrial software based on WPF (2)
- "Gold, silver and four" job hopping needs to be cautious. Can an article solve the interview?
- Hackmyvm target series (3) -visions
- 7-9 make house number 3.0 (PTA program design)
- 力扣152题乘数最大子数组
- captcha-killer验证码识别插件
猜你喜欢

Mixlab unbounded community white paper officially released
Windows platform mongodb database installation

Intel oneapi - opening a new era of heterogeneity
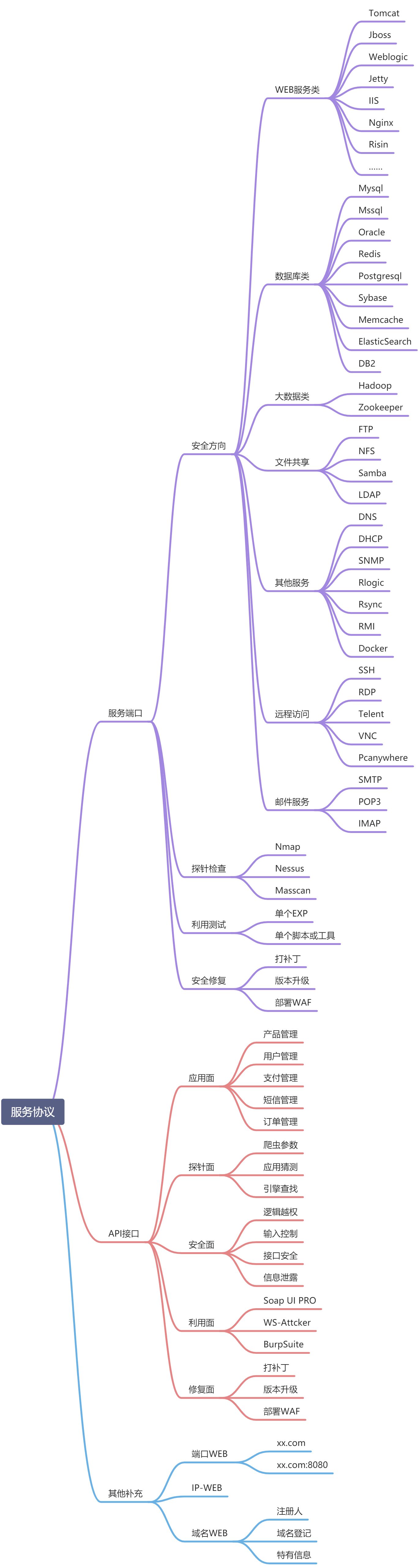
浅谈漏洞发现思路
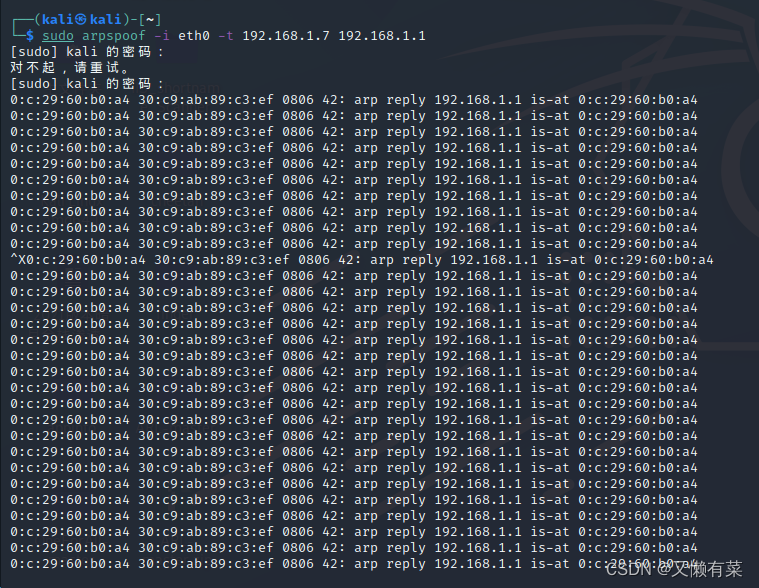
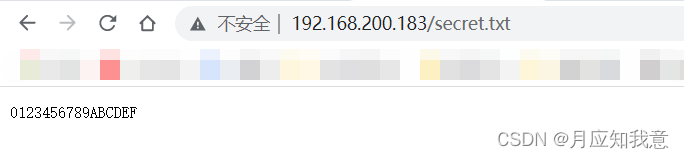
Network layer - simple ARP disconnection
HackMyvm靶机系列(2)-warrior
![[dark horse morning post] Shanghai Municipal Bureau of supervision responded that Zhong Xue had a high fever and did not melt; Michael admitted that two batches of pure milk were unqualified; Wechat i](/img/d7/4671b5a74317a8f87ffd36be2b34e1.jpg)
[dark horse morning post] Shanghai Municipal Bureau of supervision responded that Zhong Xue had a high fever and did not melt; Michael admitted that two batches of pure milk were unqualified; Wechat i
中间件漏洞复现—apache
网络基础之路由详解
Record an edu, SQL injection practice
随机推荐
Hackmyvm target series (5) -warez
实验六 继承和多态
强化学习基础记录
Beautified table style
Renforcer les dossiers de base de l'apprentissage
Detailed explanation of network foundation
List and data frame of R language experiment III
实验九 输入输出流(节选)
Xray and burp linkage mining
It's never too late to start. The tramp transformation programmer has an annual salary of more than 700000 yuan
7-4 hash table search (PTA program design)
xray與burp聯動 挖掘
[err] 1055 - expression 1 of order by clause is not in group by clause MySQL
Applet Web Capture -fiddler
HackMyvm靶機系列(3)-visions
搭建域环境(win)
Windows platform mongodb database installation
实验五 类和对象
HackMyvm靶机系列(1)-webmaster
[dark horse morning post] Shanghai Municipal Bureau of supervision responded that Zhong Xue had a high fever and did not melt; Michael admitted that two batches of pure milk were unqualified; Wechat i