Data mining - a discussion on sample imbalance in classification problems

   When I was looking at some competition cases before, I encountered the imbalance of samples , Tried different sampling methods , It doesn't work very well , So in this article, let's discuss .

1、 Is it necessary to upsample if the sample is unbalanced / Down sampling

1.1 Data preparation

   Here we generate a containing 2 Features Of 2 classification Data sets , At the same time, centralize the data 2 The distribution difference of class sample data in the sample space is relatively obvious , The code is as follows ：

import pandas as pd
import matplotlib.pyplot as plt
from random import uniform

#  The label is 0 Categories , The first feature is 0～1 Random number between , The second feature is 2～3 Random number between 
res1 = []
for i in range(50):
    res1.append([uniform(0,1), uniform(2,3), 0])

#  The label is 1 Categories , The first feature is 2～3 Random number between , The second feature is 0～1 Random number between 
res2 = []
for j in range(500):
    res2.append([uniform(2,3), uniform(0,1), 1])
    
res = res1 + res2

#  hold res convert to Dataframe, And reset the column name 
df = pd.DataFrame(res)
df.columns = ['x_1', 'x_2', 'y']

#  Draw a scatter plot of the data set 
fig = plt.figure(figsize=(10,6))
plt.scatter(df.x_1, df.x_2)
plt.xlabel('x_1')
plt.ylabel('x_2')
plt.show()

   The data generated is as follows （0、1 The proportion of categories is 1:10）：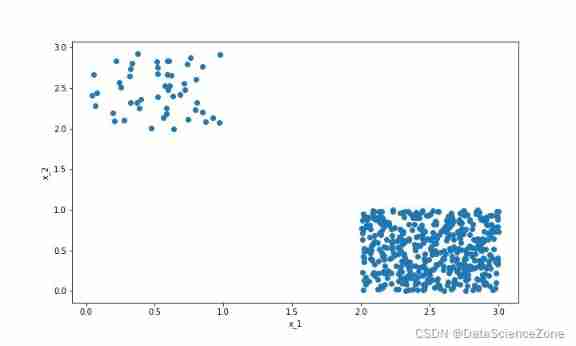

1.2 Training 、 Test the classification effect of the model

   Using support vector machine model , Classify the data , And print the evaluation matrix ：

from sklearn import svm
from sklearn.model_selection import train_test_split
from sklearn import metrics

#  there df It is generated in the previous step df, Split features and labels 
x = df.drop(columns=['y'])
y = df['y']

#  Generating training sets and test sets 
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.3, random_state=1)

#  Define and train support vector machine models 
clf = svm.SVC()
clf.fit(x_train, y_train)

#  Print the scoring matrix 
y_pred = clf.predict(x_test)
print(metrics.classification_report(y_test,y_pred))

   The printed scoring matrix is as follows ：

              precision    recall  f1-score   support

           0       1.00      1.00      1.00        19
           1       1.00      1.00      1.00       146

    accuracy                           1.00       165
   macro avg       1.00      1.00      1.00       165
weighted avg       1.00      1.00      1.00       165

   You can see that the classification effect of the model is very good .

1.3 Draw the classification interval of support vector machine

   You can also put the trained model , Draw the classification boundary

import numpy as np


res_new = np.array(res)
x_new = res_new[:,0:2]
y_new = res_new[:,2]

clf = svm.SVC()
clf.fit(x_new, y_new)


fig2 = plt.figure(figsize=(10,6))
plt.scatter(x_new[:, 0], x_new[:, 1], c=y_new, s=30, cmap=plt.cm.Paired)
ax = plt.gca()
xlim = ax.get_xlim()
ylim = ax.get_ylim()

# create grid to evaluate model
xx = np.linspace(xlim[0], xlim[1], 30)
yy = np.linspace(ylim[0], ylim[1], 30)
YY, XX = np.meshgrid(yy, xx)
xy = np.vstack([XX.ravel(), YY.ravel()]).T
Z = clf.decision_function(xy).reshape(XX.shape)

# plot decision boundary and margins
ax.contour(
    XX, YY, Z, colors="k", levels=[-1, 0, 1], alpha=0.5, linestyles=["--", "-", "--"]
)
# plot support vectors
ax.scatter(
    clf.support_vectors_[:, 0],
    clf.support_vectors_[:, 1],
    s=100,
    linewidth=1,
    facecolors="none",
    edgecolors="k",
)
plt.show()

   The resulting image is as follows ：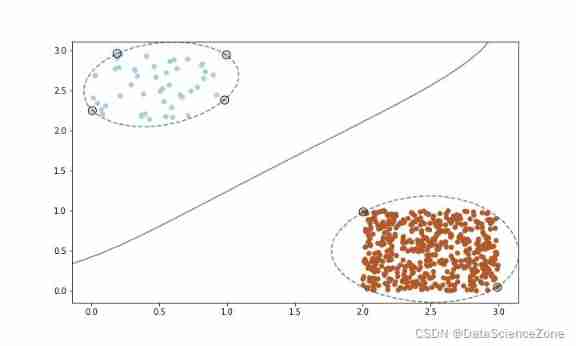

1.4 Conclusion 1

   According to the above test , So the conclusion is ： If the features in the dataset are well differentiated , The distribution of different types of samples in the sample space can be clearly distinguished , Then even if the sample is unbalanced, it will not affect the classification effect of the model , namely Features determine the upper limit of classification accuracy .

2、 On the sampling / Whether down sampling can really improve the classification effect of the model

2.1 Data preparation

   Here is also the generation contains 2 Features Of 2 classification Data sets , The code is as follows ：

#  Pour in the required modules 
import numpy as np
import matplotlib.pyplot as plt
from sklearn import svm
from sklearn.datasets import make_blobs

# we create two clusters of random points
#  establish 2 Data of class samples , The label is 0 The data of 1000 Bar record , The label is 1 The data of 100 Bar record 
n_samples_1 = 1000
n_samples_2 = 100
centers = [[0.0, 0.0], [2.0, 2.0]]
clusters_std = [1.5, 0.5]
X, y = make_blobs(
    n_samples=[n_samples_1, n_samples_2],
    centers=centers,
    cluster_std=clusters_std,
    random_state=0,
    shuffle=False,
)

2.2 Training models

   Next, train the support vector machine model , The first model uses sample data directly ; The second model modifies parameters class_weight , To label as 1 Sample up , The code is as follows ：

# fit the model and get the separating hyperplane
clf = svm.SVC(kernel="linear", C=1.0)
clf.fit(X, y)

# fit the model and get the separating hyperplane using weighted classes
wclf = svm.SVC(kernel="linear", class_weight={
    1: 10})
wclf.fit(X, y)

2.3 Draw classification boundaries

   Then draw 2 Classification boundaries of models , The code is as follows ：

# plot the samples
fig3 = plt.figure(figsize=(10,6))
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.Paired, edgecolors="k")

# plot the decision functions for both classifiers
ax = plt.gca()
xlim = ax.get_xlim()
ylim = ax.get_ylim()

# create grid to evaluate model
xx = np.linspace(xlim[0], xlim[1], 30)
yy = np.linspace(ylim[0], ylim[1], 30)
YY, XX = np.meshgrid(yy, xx)
xy = np.vstack([XX.ravel(), YY.ravel()]).T

# get the separating hyperplane
Z = clf.decision_function(xy).reshape(XX.shape)

# plot decision boundary and margins
a = ax.contour(XX, YY, Z, colors="k", levels=[0], alpha=0.5, linestyles=["-"])

# get the separating hyperplane for weighted classes
Z = wclf.decision_function(xy).reshape(XX.shape)

# plot decision boundary and margins for weighted classes
b = ax.contour(XX, YY, Z, colors="r", levels=[0], alpha=0.5, linestyles=["-"])

plt.legend(
    [a.collections[0], b.collections[0]],
    ["non weighted", "weighted"],
    loc="upper right",
)
plt.show()

2.4 Compare the classification effect of the model

   Use the model trained in the previous step , Separately predict the labels of the input data （ The data input here is still a training set ）, Then print the evaluation matrix , The code is as follows ：

from sklearn import metrics

y_pre_1 = clf.predict(X)		#  No upsampling model is used 
y_pre_2 = wclf.predict(X)		#  Use the upsampled model 

print(metrics.classification_report(y,y_pre_1))
print(metrics.classification_report(y,y_pre_2))

   The printed evaluation matrix is as follows ：

#  No upsampling model is used 
              precision    recall  f1-score   support

           0       0.96      0.98      0.97      1000
           1       0.71      0.59      0.64       100

    accuracy                           0.94      1100
   macro avg       0.84      0.78      0.81      1100
weighted avg       0.94      0.94      0.94      1100

#  Split line ----------------------------------------------
#  No upsampling model is used 
              precision    recall  f1-score   support

           0       1.00      0.90      0.95      1000
           1       0.50      0.97      0.66       100

    accuracy                           0.91      1100
   macro avg       0.75      0.94      0.81      1100
weighted avg       0.95      0.91      0.92      1100

   You can find 2 Inside the model , The label of the model after sampling is 1 The sample of , The accuracy is down , Recall rate increased .2 A model of f1-score The difference is not obvious , On the whole 2 The effect difference of the two models is not obvious .

2.5 Conclusion 2

   Summarize the test results above , We can draw ： By up sampling / Down sampling does not necessarily improve the classification effect of the model , However, it can also be sampled when training the model / Down sampling attempt .

3 summary

   Data characteristics It is the key to determine the effect of the model .

   If there is any mistake in the above discussion , Please also point out that .

  
  
Reference link ：
https://scikit-learn.org/stable/modules/generated/sklearn.svm.SVC.html#sklearn.svm.SVC
https://scikit-learn.org/stable/auto_examples/svm/plot_separating_hyperplane_unbalanced.html
https://scikit-learn.org/stable/auto_examples/svm/plot_separating_hyperplane.html#sphx-glr-auto-examples-svm-plot-separating-hyperplane-py