《统计学》第八版贾俊平第三章课后习题及答案总结

1.考点归纳

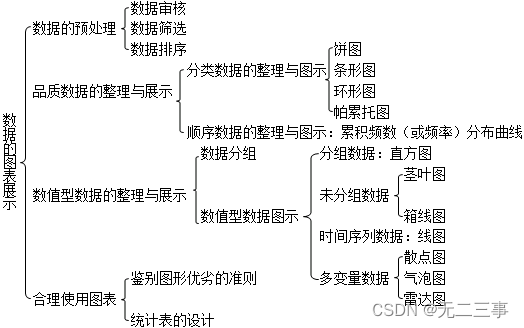
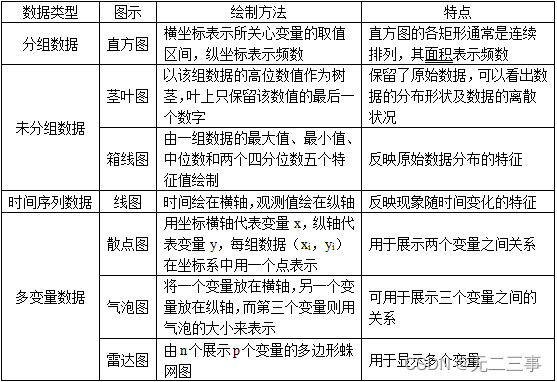
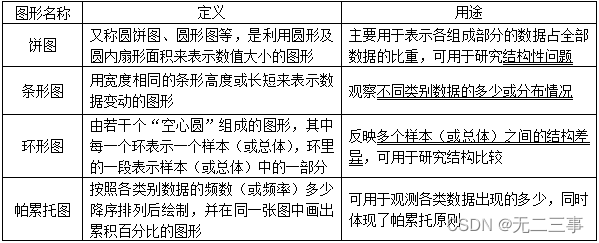
一、思考题

1数据的预处理包括哪些内容？

答：数据的预处理是在对数据分类或分组之前所做的必要处理，内容包括数据的审核、筛选、排序等。
（1）数据审核就是检查数据中是否有错误。对于通过调查取得的原始数据，主要从完整性和准确性两个方面去审核；对于通过其他渠道取得的二手数据，则应着重审核数据的适用性和时效性。
（2）数据筛选是根据需要找出符合特定条件的某类数据。
（3）数据排序是按一定顺序将数据排列，以便研究者通过浏览数据发现一些明显的特征或趋势，找到解决问题的线索。除此之外，排序还有助于对数据检查纠错，以及为重新归类或分组等提供方便。

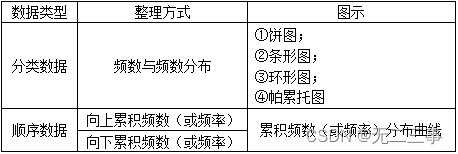
2分类数据和顺序数据的整理和图示方法各有哪些？

答：（1）分类数据的整理和图示方法

①分类数据的整理方法：首先列出分类数据所分的类别，然后计算出每一类别的频数、频率或比例、比率等，即可形成一张频数分布表；

②图示方法：条形图、帕累托图、饼图和环形图。

（2）顺序数据的整理和图示方法

①顺序数据的整理方法：首先按照一定的顺序将数据进行分类，然后计算出每一类别的频数、比例、百分比、比率等，对于顺序数据，除了可使用分类数据的整理和图示技术外，还可以计算累积频数和累积频率（百分比）；

②图示方法：条形图、饼图、帕累托图、累积频数分布图和环形图。

3数值型数据的分组方法有哪些？简述组距分组的步骤。

答：（1）数据分组的方法有单变量值分组和组距分组两种。

①单变量值分组是把每一个变量值作为一组，这种分组通常只适合离散变量，且变量值较少的情况下使用；

②在连续变量或变量值较多的情况下，通常采用组距分组。它是将全部变量值依次划分为若干个区间，并将这一区间的变量值作为一组。在组距分组中，一个组的最小值称为下限；一个组的最大值称为上限。
（2）组距分组步骤

①确定组数。组数的确定应以能够显示数据的分布特征和规律为目的。一般情况下，一组数据所分的组数不应少于5组且不多于15组，即5≤K≤15；

②确定各组的组距。组距是一个组的上限与下限的差。组距可根据全部数据的最大值和最小值及所分的组数来确定，即组距＝（最大值－最小值）÷组数；

③根据分组编制频数分布表。

4直方图与条形图有何区别？

答：直方图与条形图的区别：
（1）条形图是用条形的长度表示各类别频数的多少，其宽度则是固定的；直方图是用面积表示各组频数的多少，矩形的高度表示每一组的频数或频率，宽度则表示各组的组距，因此其高度与宽度均有意义；
（2）由于分组数据具有连续性，直方图的各矩形通常是连续排列，而条形图则是分开排列；
（3）条形图主要用于展示分类数据，而直方图则主要用于展示数值型数据。

5绘制线图应注意哪些问题？

答：绘制线图时应注意：
（1）时间一般绘在横轴，观测值绘在纵轴；
（2）一般应绘成横轴略大于纵轴的长方形，其长宽比例大致为10：7；
（3）图形过扁或过于瘦高，不仅不美观，而且会给人造成视觉上的错觉，不利于对数据变化的理解；
（4）一般情况下，纵轴数据下端应从“0”开始，以便作比较。如果数据与“0”之间的间距过大，可以采取折断的符号将纵轴折断。

6饼图和环形图有什么不同？

答：环形图中间有一个“空洞”，样本或总体中的每一部分数据用环中的一段表示。饼图只能显示一个样本或总体各部分所占的比例，而环形图则可以同时绘制多个样本或总体的数据系列，每一个样本或总体的数据系列为一个环，有利于对构成做比较研究。

7茎叶图与直方图相比有什么优点？它们的应用场合是什么？

答：（1）茎叶图与直方图相比的优点：茎叶图类似于横置的直方图，与直方图相比，茎叶图既能给出数据的分布状况，又能给出每一个原始数值，即保留了原始数据的信息。而直方图虽然能很好地显示数据的分布，但不能保留原始的数值。
（2）茎叶图与直方图的应用场合：直方图通常适用于大批量数据，茎叶图通常适用于小批量数据。

8鉴别图表优劣的准则有哪些？答：鉴别图形优劣的准则有：
（1）一张好图应当精心设计、有助于洞察问题的实质；
（2）一张好图应当使复杂的观点得到简明、确切、高效的阐述；
（3）一张好图应当能在最短的时间内以最少的笔墨给读者提供最大量的信息；
（4）一张好图应当是多维的；
（5）一张好图应当表述数据的真实情况。

9制作统计表应注意哪几个问题？

答：制作统计表时要注意以下几点：

（1）要合理安排统计表的结构，比如行标题、列标题、数据资料的位置应安排合理。当然，由于强调的问题不同，行标题和列标题可以互换，但应使统计表的横竖长度比例适当，避免出现过高或过宽的表格形式。
（2）表头一般应包括表号、总标题和表中数据的单位等内容。总标题应简明确切地概括出统计表的内容，一般需要说明统计数据的时间（When）、地点（Where）以及内容（What），即标题内容应满足3W要求。如果表中的全部数据都是同一计量单位，可在表的右上角标明。若各变量的计量单位不同，则应放在每个变量后或单列出一列标明。
（3）表中的上下两条横线一般用粗线，中间的其他线要用细线，这样使人看起来清楚、醒目。通常情况下，统计表的左右两边不封口，列标题之间在必要时可用竖线分开，而行标题之间通常不必用横线隔开。总之，表中尽量少用横竖线。表中的数据一般是右对齐，有小数点时应以小数点对齐，而且小数点的位数应统一；对于没有数据的表格单元，一般用“—”表示；一张填好的统计表不应出现空白单元格。
（4）在使用统计表时，必要时可在表的下方加上注释，特别要注意应注明数据来源，以表示对他人劳动成果的尊重，以备读者查阅使用。

二、练习题1为评价家电行业售后服务的质量，随机抽取了由100个家庭构成的一个样本。服务质量的等级分别表示为：A．好；B．较好；C．一般；D．较差；E．差。调查结果如表3-4所示。
表3-4　家电行业售后服务的质量表

要求：
（1）用Excel制作一张频数分布表。
（2）绘制一张条形图，反映评价等级的分布。
（3）绘制评价等级的帕累托图。

解：
（2）制作频数分布表，如表3-5所示。

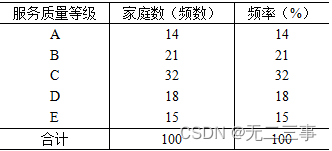
表3-5　服务质量等级评价的频数分布
（2）绘制评价等级的条形图，如图3-1所示。

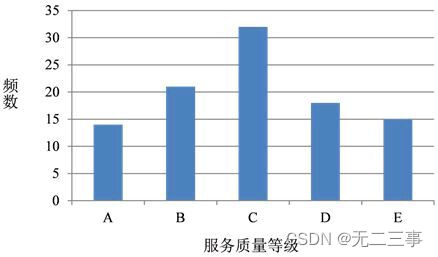
图3-1　评价等级的条形图
（4）绘制评价等级的帕累托图，如图3-2所示。

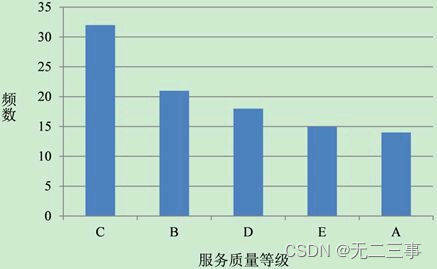
图3-2　评价等级的帕累托图

2为了确定灯泡的使用寿命，在一批灯泡中随机抽取100个进行测试，所得结果如表3-6所示。

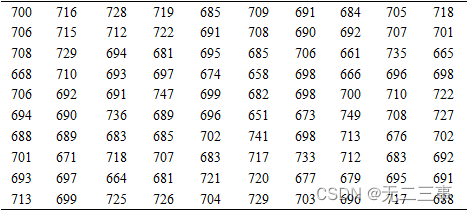
表3-6　灯泡使用寿命（单位：小时）
要求：。
（1）以组距为10进行等距分组，整理成频数分布表。
（2）根据分组数据绘制直方图，说明数据分布的特点。
（3）制作茎叶图，并与直方图作比较。

解：（1）编制频数分布表，如表3-7所示。

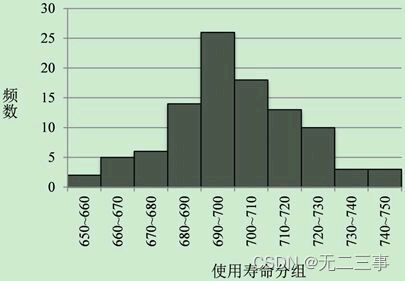
表3-7　100只灯泡使用寿命的频数分布
（3）绘制灯泡使用寿命分布的直方图，如图3-3所示。

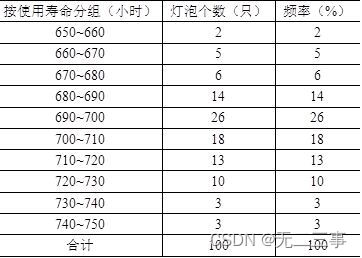
图3-3　灯泡使用寿命分布的直方图
（4）构建灯泡使用寿命分布的茎叶图，如图3-4所示。

图3-4　灯泡使用寿命分布的茎叶图
从灯泡使用寿命分布的直方图和茎叶图可以看出，灯泡使用寿命基本上是对称分布的。直方图和茎叶图所反映的分布特征是一致的，但茎叶图的好处是保留了原始数据的信息。

3一种袋装食品用生产线自动装填。每袋重量大约为50g，但由于某些原因，每袋重量不会恰好是50g。下面是随机抽取的100袋食品，测得的重量数据如表3-9所示。

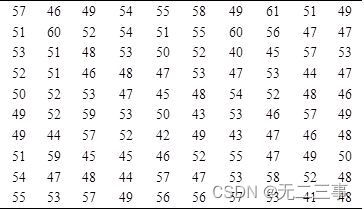
表3-9　食品重量（单位：g）

要求：
（1）构建这些数据的频数分布表。
（2）绘制频数分布的直方图。
（3）说明数据分布的特征。

答：（1）构建食品重量的频数分布表，如表3-10所示。

表3-10　食品重量的频数分布表
（2）绘制食品重量的频数分布的直方图，如图3-5所示。

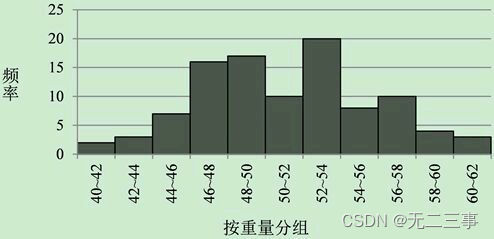
图3-5　食品重量的频数分布的直方图
（3）从直方图可以看出，食品重量的分布基本上是对称分布。

4对表3-11的数据绘制散点图。

表3-11

解：绘制散点图，如图3-6所示。

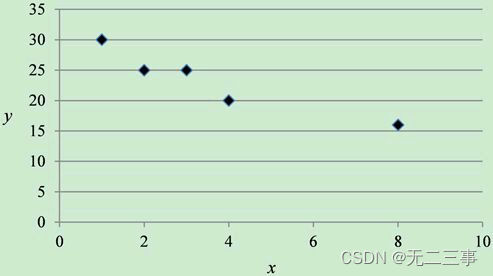
图3-6　散点图

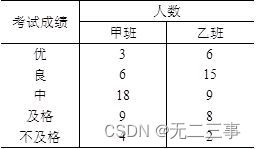
5甲、乙两个班各有40名学生，期末统计学考试成绩的分布如表3-12所示。
表3-12　甲乙两班期末统计学考试成绩

要求：
（1）根据上面的数据，画出两个班考试成绩的对比条形图和环形图。
（2）比较两个班考试成绩分布的特点。
（3）画出雷达图，比较两个班考试成绩的分布是否相似。

解：（1）绘制对比条形图，如图3-7所示。

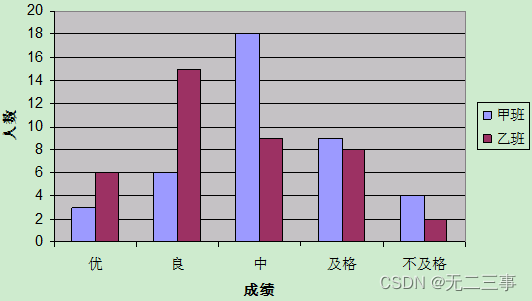
图3-7　甲乙两班期末统计学考试成绩条形图
绘制环形图，如图3-8所示（内环为甲班的成绩）。

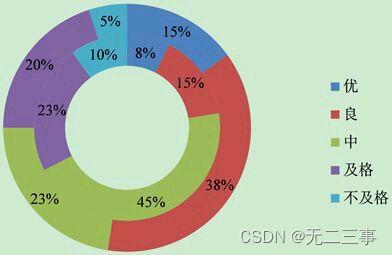
图3-8　甲乙两班期末统计学考试成绩环形图
（2）对比条形图可以看出，甲班考试成绩在中等水平的人数较多，而优秀和良好的人数则较少，不及格的人数也比乙班要多。乙班则不同，考试成绩为优秀和良好的人数较多，而中等以下的人数则较少。这说明乙班学生的平均成绩比甲班要好。从环形图的百分比中也可以清楚地看出这一点。
（3）绘制两个班考试成绩的雷达图，如图3-9所示。

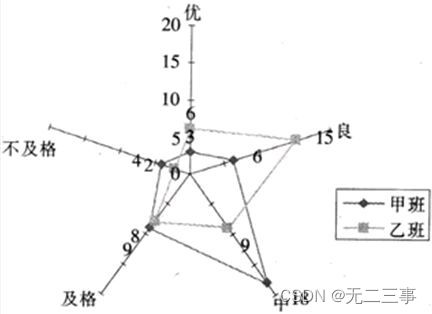
图3-9　甲乙两班期末统计学考试成绩雷达图
从雷达图的形状可以看出，两个班考试成绩没有相似性。

6.1997年我国几个主要城市各月份的平均相对湿度数据如表3-13所示。试绘制箱线图，并分析各城市平均相对湿度的分布特征。

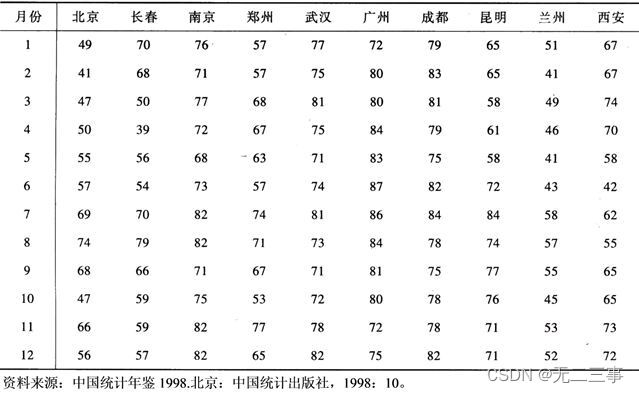
表3-13　1997年我国几个主要城市各月份的平均相对湿度

解：绘制各城市各月份的平均相对湿度的箱线图，如图3-10所示。

 
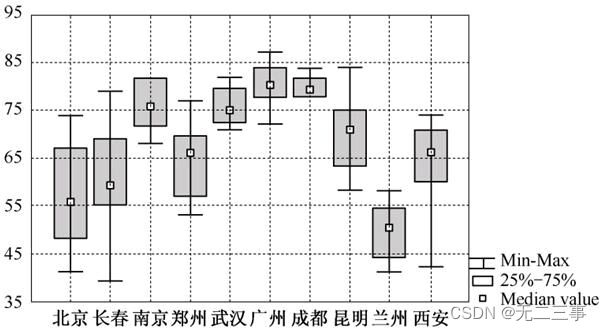
图3-10　各城市相对湿度箱线图
从箱线图可以看出，各城市的月平均相对湿度有较大差异。离散程度较大的城市主要是北京和长春（箱子较大）；离散程度较小的是成都、广州和武汉（箱子较小）；相对湿度最大的城市主要有成都、广州、南京和武汉（中位数较大）；相对湿度最小的城市是兰州（中位数较小）；相对湿度分布比较对称的城市主要是北京、武汉、广州和兰州等（中位数大体上在箱子中间，最大值和最小值与箱子的距离大体相等）；相对湿度不对称的城市主要有南京、郑州等；相对湿度存在极值的城市主要是长春和西安。