当前位置:网站首页>《统计学》第八版贾俊平第十三章时间序列分析和预测知识点总结及课后习题答案
《统计学》第八版贾俊平第十三章时间序列分析和预测知识点总结及课后习题答案
2022-07-06 09:23:00 【无二三事】
目录
一、知识框架
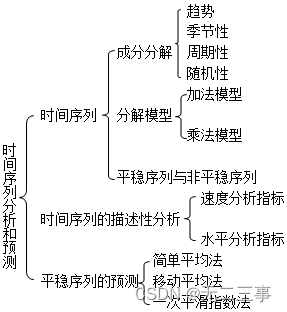
二、练习题
1是1991~2008年我国财政收入数据。采用指数曲线预测2009年的财政收入,并将实际值和预测值绘图进行比较。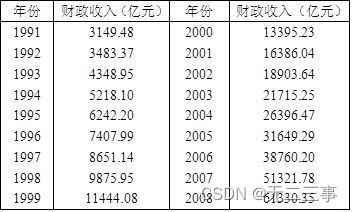
解:设指数曲线的趋势方程为Yt=b0b1t,两端取对数得ln(Yt)=ln(b0)+tln(b1)。根据最小二乘法原理,求得ln(b1)=0.1709,ln(b0)=7.8445,对应指数曲线方程为Yt=2551.6615×1.1864t。
将t=1,2,…,18代入趋势方程得到各期的预测值,将t=19代入趋势方程即可得到2009年财政收入的预测值。计算结果见
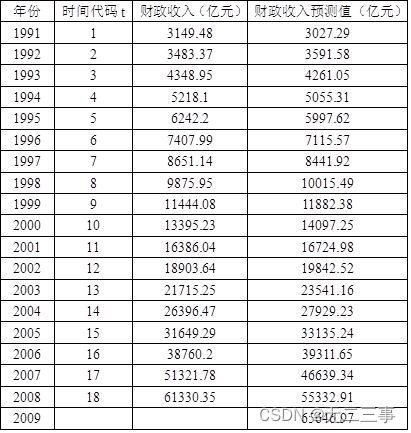
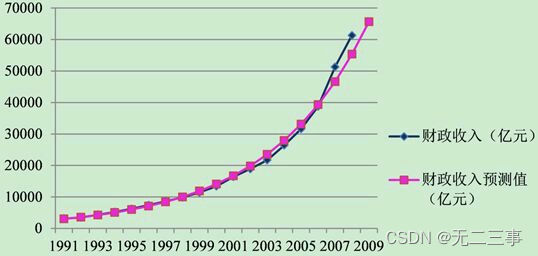
2表13-6是一家旅馆过去18个月的营业额数据。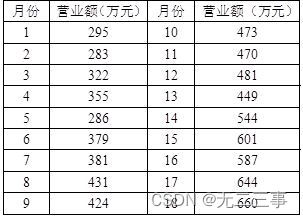
要求:
(1)用3期移动平均法预测第19个月的营业额。
(2)采用指数平滑法,分别用平滑系数α=0.3,α=0.4和α=0.5预测各月的营业额,分析预测误差,说明用哪一个平滑系数预测更合适。
(3)建立一个趋势方程预测各月的营业额,计算出估计标准误差。
解:(1)第19个月的3期移动平均预测值为:
F19=(587+644+660)/3=630.33
(2)由Excel输出的指数平滑预测值,如表所示。
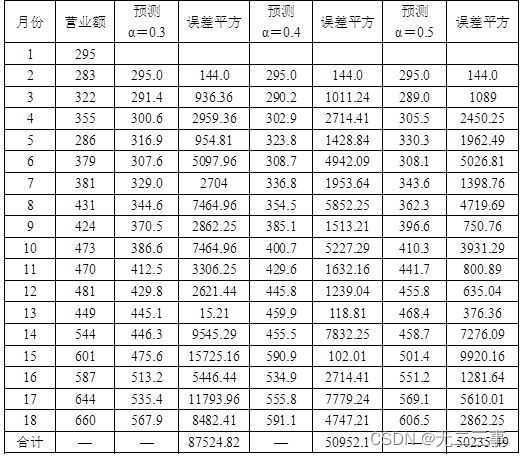
α=0.3时的预测值为:F19=0.3×660+(1-0.3)×567.9=595.5,误差平方=87524.82
α=0.4时的预测值为:F19=0.4×660+(1-0.4)×591.1=618.7,误差平方=50952.1
α=0.5时的预测值为:F19=0.5×660+(1-0.5)×606.5=633.3,误差平方=50235.49比较各误差平方可知,α=0.5更合适。
(3)根据最小二乘法,利用Excel输出的回归结果如表所示。
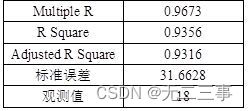
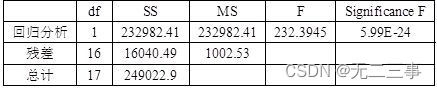

所以线性趋势方程为:Yt=239.73+21.9288t;估计标准误差SY=31.6628。
3我国1964~1999年的纱产量数据,如表13-11所示(单位:万吨)。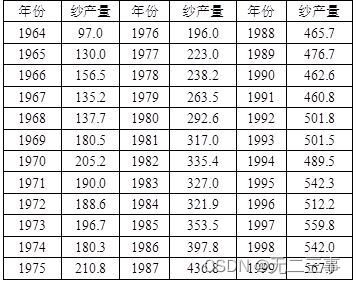
(1)绘制时间序列图描述其趋势。
(2)选择一条适合的趋势线拟合数据,并根据趋势线预测2000年的产量。
解:(1)绘制时间序列图,如图所示。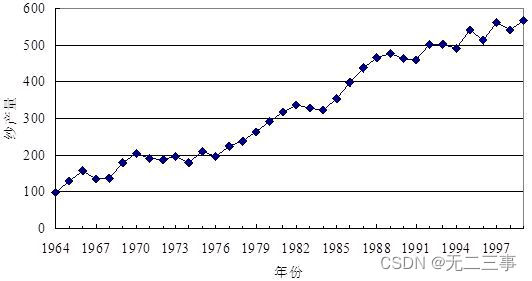
(2)从图中可以看出,纱产量具有明显的线性趋势。用Excel求得的线性趋势方程为:Yt=69.5202+13.9495t
所以2000年预测值为:Y37=69.5202+13.9495×37=585.65(万吨)
4对表13-12的数据分别拟合线性趋势线Yt=b0+b1t、二阶曲线Yt=b0+b1t+b2t2和三阶曲线Yt=b0+b1t+b2t2+b3t3,并对结果进行比较。
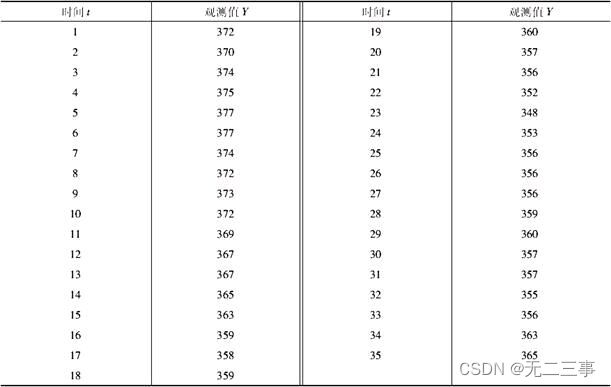 解:在求二阶曲线和三阶曲线时,首先将其线性化,然后用最小二乘法按线性回归进行求解。用Excel求得的趋势直线、二阶曲线和三阶曲线的系数,如表所示。
解:在求二阶曲线和三阶曲线时,首先将其线性化,然后用最小二乘法按线性回归进行求解。用Excel求得的趋势直线、二阶曲线和三阶曲线的系数,如表所示。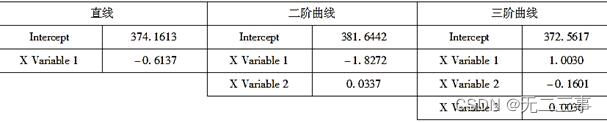
所以各趋势方程为:
线性趋势:Yt=374.1613-0.6137t
二阶曲线:Yt=381.6442-1.8272t+0.0337t2三阶曲线:Yt=372.5617+1.0030t-0.1601t2+0.0036t3
根据趋势方程求得的预测值和预测误差,如表所示。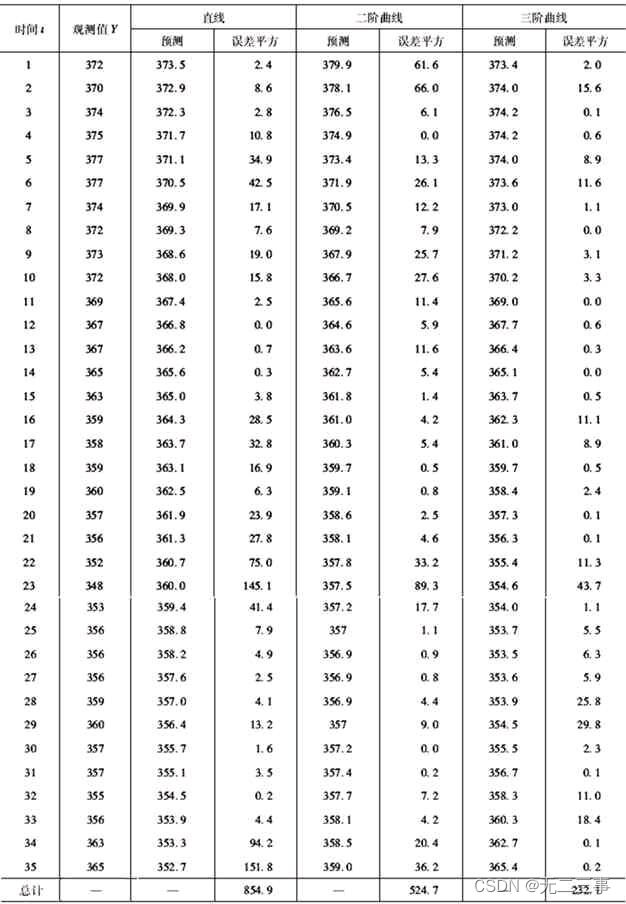
不同趋势线预测的标准误差分别为:
直线:
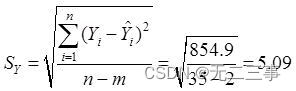
二阶曲线:
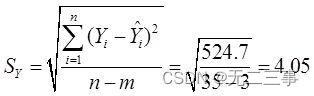
三阶曲线:
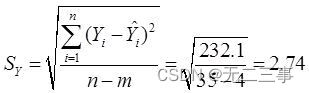
比较各预测误差可知,直线的误差最大,三阶曲线的误差最小。
从不同趋势方程的预测图(如图所示)也可以看出,三阶曲线与原序列的拟合最好。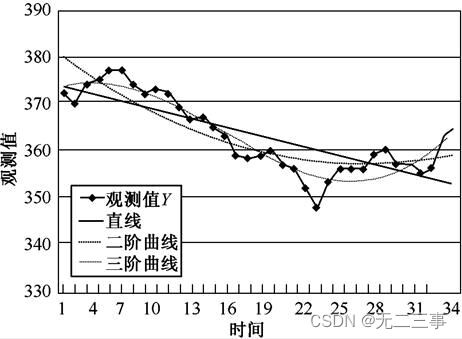
5一家贸易公司主要经营产品的外销业务,为了合理地组织货源,需要了解外销订单的变化状况。表是2011~2015年各月份的外销订单金额(单位:万元)。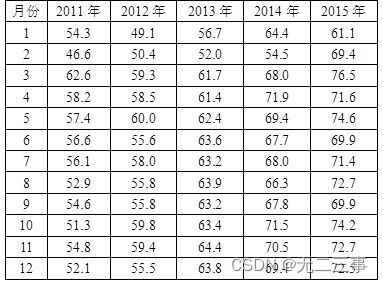
要求:
(1)根据各年的月份数据绘制趋势图,说明该时间序列的特点。
(2)要计算各月份的预测值,你认为应该采取什么方法?
(3)选择你认为合适的方法预测2016年1月份的外销订单金额。
解:(1)绘制趋势图,如图所示。
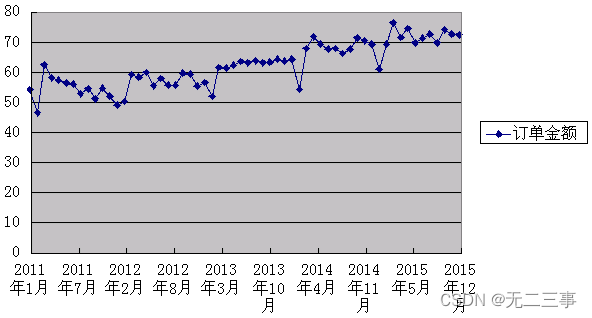
从趋势图可以看出,每一年的各月份数据没有趋势存在,但从2011~2015年的变化看,订单金额存在一定的线性趋势。
(2)由于是预测各月份的订单金额,因此采用移动平均法或指数平滑法比较合适。
(3)用Excel采用12项移动平均法预测的结果为:F2016/1=71.4(万元)。
用Excel采用指数平滑法(α=0.4)预测的预测结果为:F2016/1=72.5(万元)。
6表13-16是一家大型百货公司最近几年各季度的销售额数据(单位:万元)。对这一时间序列的构成要素进行分解,计算季节指数,剔除季节变动,计算剔除季节变动后的趋势方程。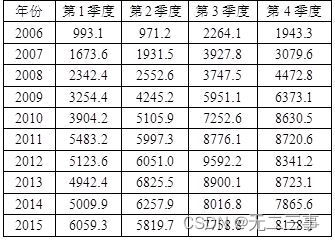
解:按季平均法计算季节指数,取移动平均项数等于周期长度,即k=4,由于移动项数是偶数,所以要做两次移动平均。
例如:2006年第一次移动平均的结果为:
T2006,2.5=(y2006,1+y2006,2+y2006,3+y2006,4)/4
T2006,3.5=(y2006,2+y2006,3+y2006,4+y2006,1)/4
……
则第二次移动平均的结果为:
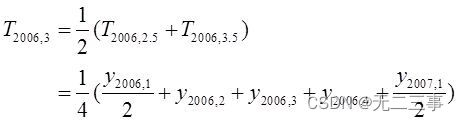
……
即2006年第3季度的移动平均数为:
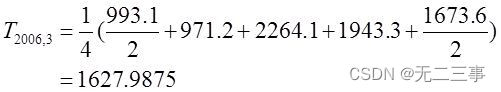
故2006年第3季度的季节比率为:
y2006,3/T2006,3=2264.1/1627.9875=1.3907
同理2006年第4季度的移动平均数为:
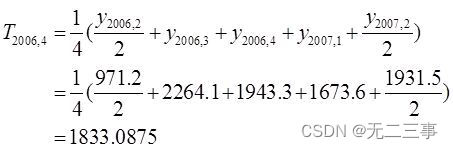
故2006年第4季度的季节比率为:
y2006,4/T2006,4=1943.3/1833.0875=1.0601
同理可得其他月份的移动平均数,进而可得相应的季节比率,最后即可求得季节指数。计算出季节指数后,将各实际观察值分别处除以相应的季节指数,从而剔除季节变动,计算公式为:y/S=(T×S×I)/S=T×I。计算结果如表所示。
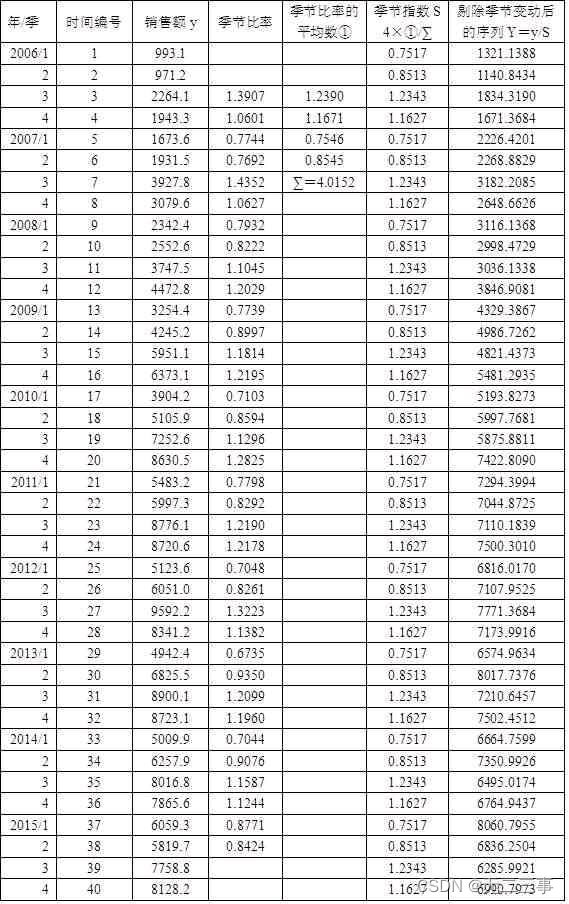
绘制季节变动图,如图所示,从图中可以看出旺季是第3季度,淡季是第1季度。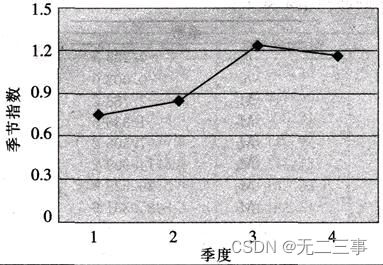
绘制剔除季节变动后销售额及其趋势图,如图所示。
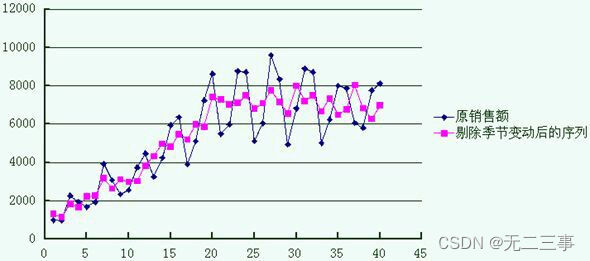
由图可知,可以用一元线性模型来预测各季度的销售额,设趋势方程为:Yt=b0+b1t,由Excel可得:b0=2043.92,b1=163.7064。所以剔除季节变动后销售额的趋势方程为:Yt=2043.92+163.7064t
边栏推荐
- Interpretation of iterator related "itertools" module usage
- Detailed explanation of network foundation
- 内网渗透之内网信息收集(五)
- Hackmyvm target series (2) -warrior
- . How to upload XMIND files to Jinshan document sharing online editing?
- Harmonyos JS demo application development
- List and data frame of R language experiment III
- [err] 1055 - expression 1 of order by clause is not in group by clause MySQL
- 强化学习基础记录
- 7-7 7003 combination lock (PTA program design)
猜你喜欢
攻防世界MISC练习区(SimpleRAR、base64stego、功夫再高也怕菜刀)
图书管理系统
循环队列(C语言)
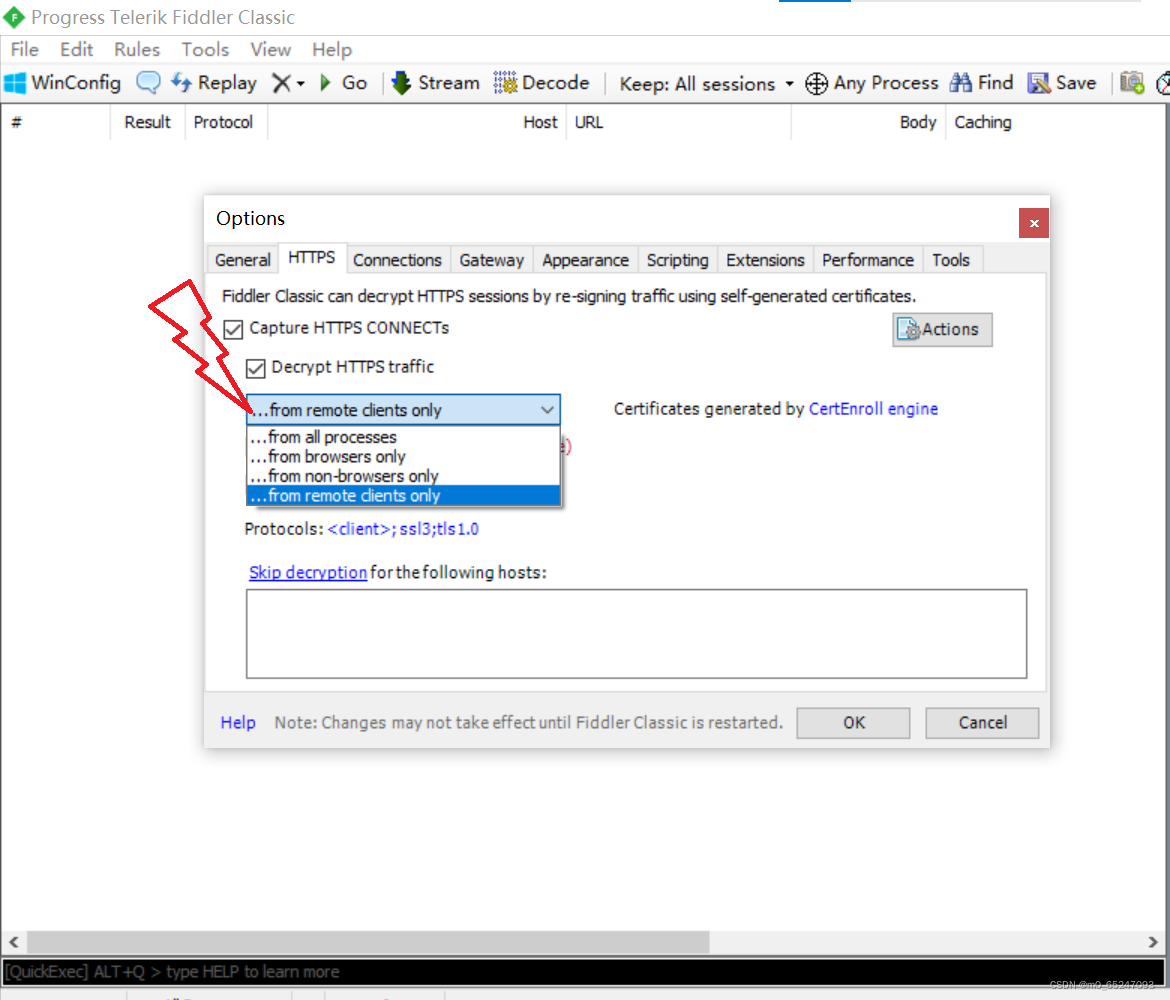
Applet Web Capture -fiddler
Callback function ----------- callback
List and data frame of R language experiment III
Xray and burp linkage mining

Attack and defense world misc practice area (simplerar, base64stego, no matter how high your Kung Fu is, you are afraid of kitchen knives)
附加简化版示例数据库到SqlServer数据库实例中

Strengthen basic learning records
随机推荐
[insert, modify and delete data in the headsong educator data table]
【头歌educoder数据表中数据的插入、修改和删除】
C language file operation
XSS之冷门事件
[dark horse morning post] Shanghai Municipal Bureau of supervision responded that Zhong Xue had a high fever and did not melt; Michael admitted that two batches of pure milk were unqualified; Wechat i
7-6 local minimum of matrix (PTA program design)
[MySQL database learning]
HackMyvm靶机系列(5)-warez
7-14 error ticket (PTA program design)
内网渗透之内网信息收集(四)
Record an API interface SQL injection practice
Attack and defense world misc practice area (simplerar, base64stego, no matter how high your Kung Fu is, you are afraid of kitchen knives)
[VMware abnormal problems] problem analysis & Solutions
Hackmyvm target series (1) -webmaster
强化学习基础记录
网络基础之路由详解
JDBC transactions, batch processing, and connection pooling (super detailed)
搭建域环境(win)
DVWA (5th week)
强化学习基础记录