当前位置:网站首页>1143_ SiCp learning notes_ Tree recursion
1143_ SiCp learning notes_ Tree recursion
2022-07-06 13:50:00 【grey_ csdn】
All learning summary :GitHub - GreyZhang/g_SICP: learn SICP and hack lisp.

A typical example of tree recursion is the solution of Fibonacci sequence , The above is a simple definition rule description . This description can be easily converted into a recursive function by code , The last screenshot of the above document is lisp How to implement .
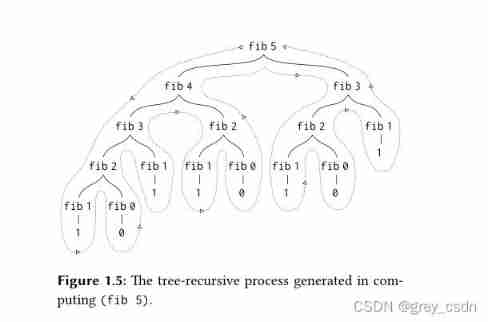
If the replacement model is used for expansion , This is the solution process of Fibonacci sequence . It can be seen from here that , Half the work is actually repetitive . In fact, it can be analyzed from the characteristics of the code itself , Because every recursion calls the function twice .

This is an optimization of Fibonacci sequence solution , In fact, the optimization method is mainly aimed at the iterative part in the previous formula . In previous software design , The state saving and other work of these two parts are actually completely entrusted to the parser . And the improved way , Make a transition between the two maintenance states , In fact, the saving of some temporary information is not completely handled by the parser, but put into memory . The design of software is actually very easy to understand .
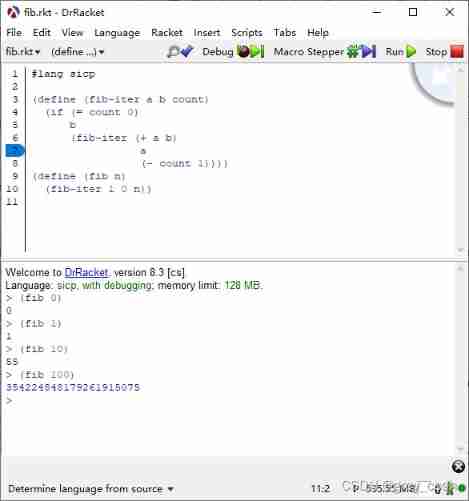
This is a test of the above software design . Equivalent functions can also be easily used python To do a writing test .
def fib(n):
if n <= 1:
return n
else:
return fib(n - 1) + fib(n - 2)
def fib_iter(a, b, n):
if n == 0:
return b
else:
return fib_iter(a + b, a, n - 1)
def new_fib(n):
return fib_iter(1, 0, n)
The computational effect of both languages is the same . I also compared the solution method with the first scheme , Solve in the computer fib(100) The process is very long . And the improved way , In fact, it has good execution efficiency , Whether it's lisp still python.

Here is another classic question : The combination of coins . The disassembly of this problem is divided into two steps , Described as the colored part above . About this description , In my own understanding, I should consider this : All the combination methods actually have 2 Kind of , One is that the first kind of coins are not used ; The other is the case of using at least one coin of the first kind . Then the case of using at least one coin of the first kind can be considered as the total amount minus the face value of one coin of the first kind , Any combination of the remaining amounts . such , It's easy to build the following recursive program .

such , Basically finished reading the content of tree recursion . Through the study of this chapter , I still see a useful way of thinking . however , The realization of many laws or methods is actually supported by certain data theory to a great extent . look , Mathematics is also a very important tool and method .
边栏推荐
- 记一次猫舍由外到内的渗透撞库操作提取-flag
- C language Getting Started Guide
- 重载和重写的区别
- Differences among fianl, finally, and finalize
- Miscellaneous talk on May 14
- 实验九 输入输出流(节选)
- Have you encountered ABA problems? Let's talk about the following in detail, how to avoid ABA problems
- (original) make an electronic clock with LCD1602 display to display the current time on the LCD. The display format is "hour: minute: Second: second". There are four function keys K1 ~ K4, and the fun
- 杂谈0516
- Zatan 0516
猜你喜欢
Mortal immortal cultivation pointer-1
hashCode()与equals()之间的关系
![[dark horse morning post] Shanghai Municipal Bureau of supervision responded that Zhong Xue had a high fever and did not melt; Michael admitted that two batches of pure milk were unqualified; Wechat i](/img/d7/4671b5a74317a8f87ffd36be2b34e1.jpg)
[dark horse morning post] Shanghai Municipal Bureau of supervision responded that Zhong Xue had a high fever and did not melt; Michael admitted that two batches of pure milk were unqualified; Wechat i
编写程序,模拟现实生活中的交通信号灯。
![[au cours de l'entrevue] - Comment expliquer le mécanisme de transmission fiable de TCP](/img/d6/109042b77de2f3cfbf866b24e89a45.png)
[au cours de l'entrevue] - Comment expliquer le mécanisme de transmission fiable de TCP

This time, thoroughly understand the MySQL index

1. First knowledge of C language (1)

Using spacedesk to realize any device in the LAN as a computer expansion screen

Mortal immortal cultivation pointer-2
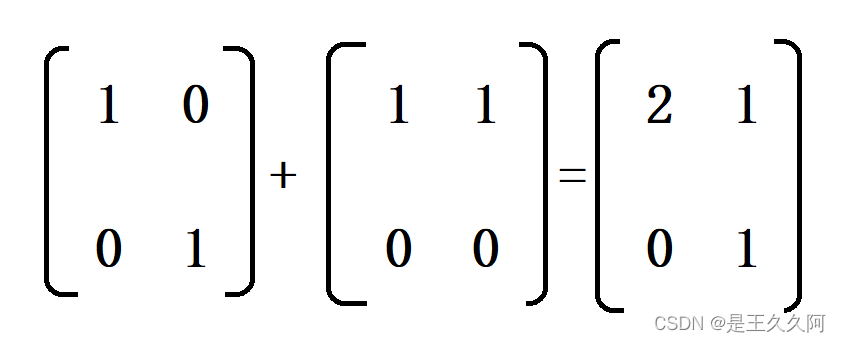
1. C language matrix addition and subtraction method
随机推荐
关于双亲委派机制和类加载的过程
记一次猫舍由外到内的渗透撞库操作提取-flag
【毕业季·进击的技术er】再见了,我的学生时代
Caching mechanism of leveldb
为什么要使用Redis
[中国近代史] 第六章测验
Custom RPC project - frequently asked questions and explanations (Registration Center)
甲、乙机之间采用方式 1 双向串行通信,具体要求如下: (1)甲机的 k1 按键可通过串行口控制乙机的 LEDI 点亮、LED2 灭,甲机的 k2 按键控制 乙机的 LED1
[the Nine Yang Manual] 2022 Fudan University Applied Statistics real problem + analysis
Programme de jeu de cartes - confrontation homme - machine
编写程序,模拟现实生活中的交通信号灯。
MySQL锁总结(全面简洁 + 图文详解)
[au cours de l'entrevue] - Comment expliquer le mécanisme de transmission fiable de TCP
Beautified table style
稻 城 亚 丁
仿牛客技术博客项目常见问题及解答(三)
Record a penetration of the cat shed from outside to inside. Library operation extraction flag
Read only error handling
Leetcode.3 无重复字符的最长子串——超过100%的解法
String abc = new String(“abc“),到底创建了几个对象