当前位置:网站首页>L2-006 tree traversal (25 points)
L2-006 tree traversal (25 points)
2022-07-06 11:26:00 【%xiao Q】
subject
Given a binary tree's post order traversal and middle order traversal , Please output the sequence of its sequence traversal . It is assumed that the key values are all positive integers which are not equal to each other .
Input format :
The first line of input gives a positive integer N(≤30), Is the number of nodes in a binary tree . The second line gives the sequence of traversal . The third line gives the order traversal sequence . Numbers are separated by spaces .
Output format :
Output the sequence traversal sequence of the tree in one line . Between the numbers 1 Space separation , There must be no extra space at the beginning and end of the line .
sample input :
7
2 3 1 5 7 6 4
1 2 3 4 5 6 7
sample output :
4 1 6 3 5 7 2
analysis
In this problem, we need to know how to build a tree when we know the middle order traversal and post order traversal of a binary tree , Here we can do this , The last node of subsequent traversal must be the root node , Then find the node in the middle order traversal , According to the characteristics of the middle order traversal, the left and right subtrees can be separated , Then in recursive left subtree and with subtree , Do the same thing .
Then there is program traversal , It's directly used here bfs Search it .
Reference code :
#include <iostream>
#include <cstdio>
#include <set>
#include <vector>
#include <cstring>
#include <cmath>
#include <queue>
#include <stack>
#include <algorithm>
#include <unordered_map>
#define LL long long
#define rep(i, a, b) for(int i = a; i <= b; i++)
#define reps(i, a, b) for(int i = a; i < b; i++)
#define pre(i, a, b) for(int i = b; i >= a; i--)
using namespace std;
const int N = 10010;
int pos, n;
int pre[N], in[N], post[N];
struct node
{
int l, r, w;
}T[N];
// Build up trees
void creat(int inl, int inr, int u)
{
if(inl > inr) return ;
// puts("hh");
// cout << u << endl;
T[u].w = post[pos--];
T[u].l = 2 * u, T[u].r = 2 * u + 1;
int mid;
for(mid = inl; mid <= inr; mid++)
if(T[u].w == in[mid]) break;
// Must recurse right subtree first , Because some points in front of the root node of subsequent traversal must be points of the right subtree ,
// And we are looking for recursion according to the root section of subsequent traversal moving forward gradually
creat(mid + 1, inr, 2 * u + 1);
creat(inl, mid - 1, 2 * u);
}
// Sequence traversal
void bfs()
{
int idx = 0;
queue<int> q;
q.push(1);
while(q.size())
{
node t = T[q.front()];
q.pop();
if(!idx) cout << t.w;
else cout << " " << t.w;
idx++;
if(T[t.l].w != -1) q.push(t.l);
if(T[t.r].w != -1) q.push(t.r);
}
}
int main()
{
cin >> n;
rep(i, 1, n) cin >> post[i];
rep(i, 1, n) cin >> in[i];
memset(T, -1, sizeof T);
pos = n;
creat(1, n, 1);
bfs();
cout << endl;
return 0;
}
边栏推荐
- DICOM: Overview
- LeetCode #461 汉明距离
- Request object and response object analysis
- ImportError: libmysqlclient. so. 20: Cannot open shared object file: no such file or directory solution
- ES6 let and const commands
- AcWing 1298.曹冲养猪 题解
- AcWing 179. Factorial decomposition problem solution
- Rhcsa certification exam exercise (configured on the first host)
- Learn winpwn (3) -- sEH from scratch
- MySQL与c语言连接(vs2019版)
猜你喜欢
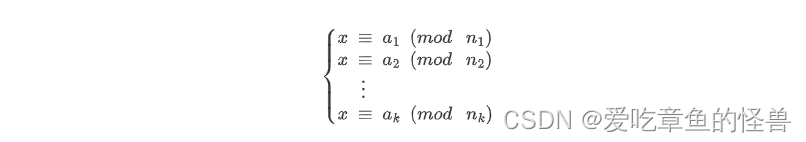
AcWing 1298.曹冲养猪 题解

In the era of DFI dividends, can TGP become a new benchmark for future DFI?
![[download app for free]ineukernel OCR image data recognition and acquisition principle and product application](/img/1b/ed39a8b9181660809a081798eb8a24.jpg)
[download app for free]ineukernel OCR image data recognition and acquisition principle and product application
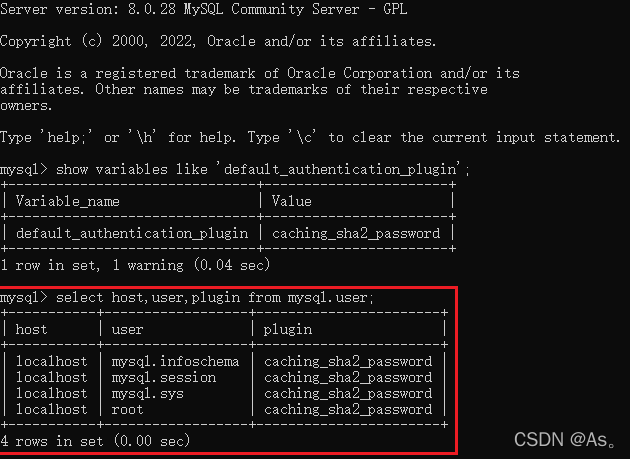
连接MySQL数据库出现错误:2059 - authentication plugin ‘caching_sha2_password‘的解决方法

快来走进JVM吧

Rhcsa certification exam exercise (configured on the first host)

One click extraction of tables in PDF
Picture coloring project - deoldify
Valentine's Day flirting with girls to force a small way, one can learn
Image recognition - pyteseract TesseractNotFoundError: tesseract is not installed or it‘s not in your path
随机推荐
库函数--(持续更新)
QT creator design user interface
Windows下安装MongDB教程、Redis教程
Solve the problem of installing failed building wheel for pilot
01 project demand analysis (ordering system)
记某公司面试算法题:查找一个有序数组某个数字出现的次数
01项目需求分析 (点餐系统)
天梯赛练习集题解LV1(all)
Machine learning -- census data analysis
QT creator specifies dependencies
Double to int precision loss
Software testing - interview question sharing
Asp access Shaoxing tourism graduation design website
When you open the browser, you will also open mango TV, Tiktok and other websites outside the home page
Niuke novice monthly race 40
安全测试涉及的测试对象
JDBC principle
In the era of DFI dividends, can TGP become a new benchmark for future DFI?
Codeforces Round #753 (Div. 3)
AcWing 1298. Solution to Cao Chong's pig raising problem