Explanation of parallel search set theory and code implementation

One 、 Concept

And lookups are tree like data structures , It is mainly used to solve some problems The problem of element grouping . Used to deal with some Disjoint Set Of Merge as well as Inquire about problem

The idea of joint search set is to represent the whole forest with an array , The root node of the tree uniquely identifies a collection , As long as we find the root of an element , You can determine which set it is in

Two 、 And look up the construction process

Let's first explain the construction process of the search set

 Father     Son 
1     3
1     2
5     4
2     4
6     8
8     7

Let's assume that the above nodes are in a set , On the left is the parent node , On the right is the child node

For the first four groups of data , We construct the following structure

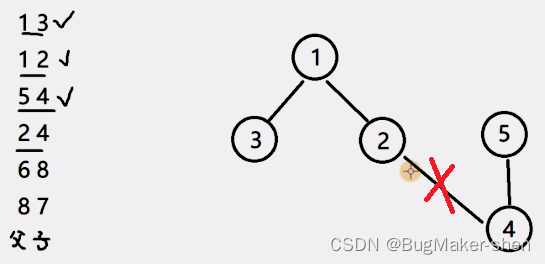
There is a problem , According to the first 4 When constructing a set with group data , Should put the 4 The root node of the tree is the same as 2 The root node of the tree is connected , The correct set structure is as follows ：

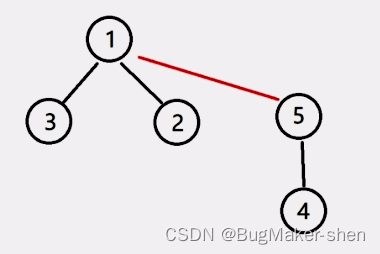
In the process of constructing and searching sets , It's not simply connecting two nodes , Instead, connect the root node of the tree where the node is located

Determine whether two nodes are in a set , Judge whether the root node of the tree where these two nodes are located is the same

We then construct a set of the last two sets of data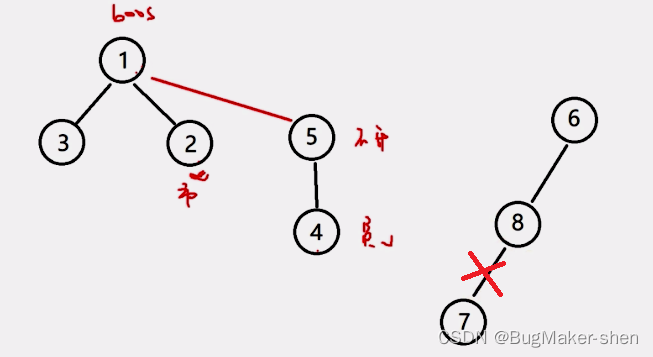

The above kind of direct handle 7 Put it in 8 The following is wrong , We just said , Merging two sets is to merge the root nodes of two trees .7 Become the root node of a tree alone , and 6 A merger , The correct combination is as follows ：

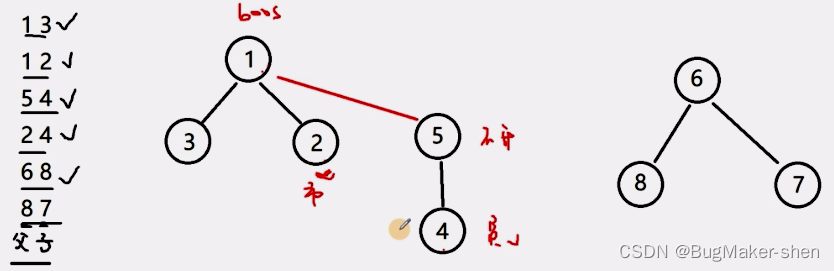
Through the above construction process , Here is a summary ：

• In the process of constructing and searching sets , It's not simply connecting two nodes , Instead, connect the root node of the tree where the node is located （ Don't care about the parent-child relationship of the root node ）
• Determine whether two nodes are in a set , Judge whether the root node of the tree where these two nodes are located is the same

3、 ... and 、 Code implementation

When implemented on code , Whether merging or querying , We need to find the root node of the tree where the node is located , Therefore, you need to record the parent node

The main idea ： The position of array elements corresponding to each node , Store the number of its parent node

How to initialize ？

Because we say that the root node of the tree where each independent node is located is itself , So we initialize with its own node number

When did you find the roots ？

When x = arr[x] When equal , Indicates that its parent node is itself , It means that the root of the tree is itself

The initialization of parallel search set is as follows ：

The forest we constructed is represented by union search set as follows

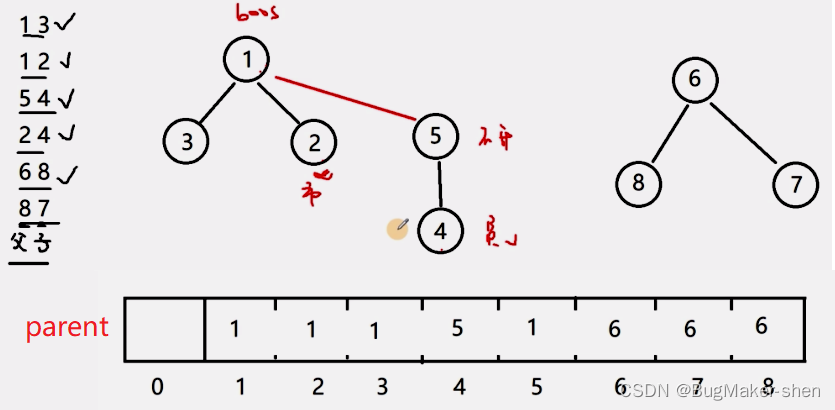
Traversal array , By comparing whether the element value and subscript are the same, we can get and check how many tree roots there are in the set . You can also see from the picture , node 1 and 6 It's the root

#include <iostream>

using namespace std;

const int SIZE = 9;
int parent[SIZE];


//  return x The number of the root node of the tree 
int find_root(int x) {
    
	if (x <= 0 || x >= SIZE) {
    
		return -1;
	}
	while (x != parent[x]) {
    
		x = parent[x];
	}
	return x;
}

//  Recursive version of the query 
int cur_find_root(int x) {
    
	if (x <= 0 || x >= SIZE) {
    
		return -1;
	}
	if (x == parent[x]) {
    
		return x;
	}
	else {
    
		return cur_find_root(parent[x]);
	}
}

//  Merge x and y Where the collection is 
void merge(int x, int y) {
    
	x = find_root(x);
	y = find_root(y);
	if (x != y) {
    
		// x and y In a set, there is no need to merge , If you are not in a set, you need to merge 
		parent[y] = x;
		// parent[x] = y;
	}
}

int main() {
    
	for (int i = 0; i < SIZE; i++) {
    
		parent[i] = i;
	}

	int x, y;
	for (int i = 0; i < 6; i++) {
    
		cin >> x >> y;
		merge(x, y);
	}
	cout<<(find_root(2) == find_root(8) ? "YES" : "NO")<<endl;
	return 0;
}