当前位置:网站首页>Explain NN in pytorch in simple terms CrossEntropyLoss
Explain NN in pytorch in simple terms CrossEntropyLoss
2022-07-05 09:06:00 【aelum】
Author's brief introduction : Non Coban transcoding , We are constantly enriching our technology stack
️ Blog home page :https://raelum.blog.csdn.net
Main areas :NLP、RS、GNN
If this article helps you , Can pay attention to ️ + give the thumbs-up + Collection + Leaving a message. , This will be the biggest motivation for my creation

Catalog
One 、 Preface
nn.CrossEntropyLoss It is often used as the loss function of multi classification problems ( Readers who don't know about cross entropy can see mine This article ), This article will focus on PyTorch Of Official documents Explain the important knowledge points one by one ( I won't explain everything ).
import torch
import torch.nn as nn
Two 、 Theoretical basis
about C ( C > 2 ) C\,(C>2) C(C>2) Classification problem , Don't think about it first batch The circumstances of , Set the output of neural network ( Not yet Softmax) by { x c } c = 1 C \{x_c\}_{c=1}^C { xc}c=1C, after Softmax Get back
q i = exp ( x i ) ∑ c = 1 C exp ( x c ) q_i=\frac{\exp(x_i)}{\sum_{c=1}^C\exp(x_c)} qi=∑c=1Cexp(xc)exp(xi)
Thus, the cross entropy loss of this sample is
H ( p , q ) = − ∑ i = 1 C p i log q i = − ∑ i = 1 C p i log exp ( x i ) ∑ c = 1 C exp ( x c ) H(p,q)=-\sum_{i=1}^C p_i\log q_i=-\sum_{i=1}^C p_i\log\frac{\exp(x_i)}{\sum_{c=1}^C\exp(x_c)} H(p,q)=−i=1∑Cpilogqi=−i=1∑Cpilog∑c=1Cexp(xc)exp(xi)
among ( p 1 , p 2 , ⋯ , p C ) (p_1,p_2,\cdots,p_C) (p1,p2,⋯,pC) yes One-Hot vector .
You may as well make p y = 1 ( y ∈ { 1 , 2 , ⋯ , C } ) p_y=1\,(y\in\{1,2,\cdots,C\}) py=1(y∈{ 1,2,⋯,C}), Others are 0 0 0, So the above formula becomes
H ( p , q ) = − log exp ( x y ) ∑ c = 1 C exp ( x c ) H(p,q)=-\log\frac{\exp(x_y)}{\sum_{c=1}^C\exp(x_c)} H(p,q)=−log∑c=1Cexp(xc)exp(xy)
Now consider batch The circumstances of , Might as well set batch size by N N N, The output of the neural network is { x n c } n c , n = 1 , ⋯ , N , c = 1 , ⋯ , C \{x_{nc}\}_{nc},\;n=1,\cdots,N,\;c=1,\cdots,C { xnc}nc,n=1,⋯,N,c=1,⋯,C, The first n n n The real category of samples is recorded as y n ( y n ∈ { 1 , 2 , ⋯ , C } ) y_n\,(y_n\in\{1,2,\cdots,C\}) yn(yn∈{ 1,2,⋯,C}), The first n n n The cross entropy loss of samples is recorded as l n l_n ln, Then follow the above formula
l n = − log exp ( x n , y n ) ∑ c = 1 C exp ( x n c ) l_n=-\log \frac{\exp(x_{n,y_n}{})}{\sum_{c=1}^C\exp(x_{nc})} ln=−log∑c=1Cexp(xnc)exp(xn,yn)
Next, let's discuss some special situations . When Data imbalance when ( The number of samples in a certain class is particularly large , The number of samples in the other category is particularly small ), We need to arrange a weight for each kind of loss to balance . The weight of w = ( w 1 , w 2 , ⋯ , w C ) \boldsymbol{w}=(w_1,w_2,\cdots,w_C) w=(w1,w2,⋯,wC).
The model is easy in the one with the largest number of samples ( Or a few ) Over fitting on class , So for those classes with a small number of samples , We need to set a higher weight , In this way, once the model makes an error in predicting the labels of these classes , Will be punished more
After arranging the weight , The corresponding loss is
l n = − w y n log exp ( x n , y n ) ∑ c = 1 C exp ( x n c ) l_n=-w_{y_n}\log \frac{\exp(x_{n,y_n}{})}{\sum_{c=1}^C\exp(x_{nc})} ln=−wynlog∑c=1Cexp(xnc)exp(xn,yn)
After calculating l 1 , l 2 , ⋯ , l N l_1,l_2,\cdots,l_N l1,l2,⋯,lN after , We can put them all at once All return ( Corresponding reduction=none), You can also return their mean value ( Corresponding reduction=mean), You can also return their and ( Corresponding reduction=sum):
ℓ = { ( l 1 , ⋯ , l N ) , reduction=none ∑ n = 1 N l n / ∑ n = 1 N w y n , reduction=mean ∑ n = 1 N l n , reduction=sum \ell=\begin{cases} (l_1,\cdots,l_N),&\text{reduction=none} \\ \sum_{n=1}^N l_n/\sum_{n=1}^N w_{y_n},&\text{reduction=mean} \\ \sum_{n=1}^N l_n,&\text{reduction=sum} \\ \end{cases} ℓ=⎩⎪⎨⎪⎧(l1,⋯,lN),∑n=1Nln/∑n=1Nwyn,∑n=1Nln,reduction=nonereduction=meanreduction=sum
stay NLP Tasks , We often add filler elements to the end of each sequence , In this way, sequences of different lengths can be loaded in batches . During training , We don't want the filler elements predicted by the network to be included in the loss function . It is advisable to set the index of filler element in the thesaurus as i i i, Then deal with l n l_n ln Make the following amendments :
l n = − w y n ⋅ I ( y n ≠ i ) ⋅ log exp ( x n , y n ) ∑ c = 1 C exp ( x n c ) , where I ( x ) = { 1 , x is True 0 , x is False l_n=-w_{y_n}\cdot \mathbb{I}(y_n\neq i)\cdot\log \frac{\exp(x_{n,y_n}{})}{\sum_{c=1}^C\exp(x_{nc})},\qquad \text{where}\; \mathbb{I}(x)= \begin{cases} 1,&x\; \text{is True} \\ 0,&x\; \text{is False} \end{cases} ln=−wyn⋅I(yn=i)⋅log∑c=1Cexp(xnc)exp(xn,yn),whereI(x)={ 1,0,xis Truexis False
in addition , In this scenario reduction=mean The corresponding loss becomes
ℓ = ∑ n = 1 N l n ∑ n = 1 N w y n ⋅ I ( y n ≠ i ) \ell=\sum_{n=1}^N\frac{l_n}{\sum_{n=1}^Nw_{y_n}\cdot \mathbb{I}(y_n\neq i)} ℓ=n=1∑N∑n=1Nwyn⋅I(yn=i)ln
It should be noted that , stay PyTorch in y n ∈ { 0 , 1 , ⋯ , C − 1 } y_n\in\{0,1,\cdots,C-1\} yn∈{ 0,1,⋯,C−1}, Here we use { 1 , 2 , ⋯ , C } \{1,2,\cdots,C\} { 1,2,⋯,C} In order to connect the context more naturally
3、 ... and 、 main parameter
nn.CrossEntropyLoss The main parameters are as follows :
nn.CrossEntropyLoss(weight=None, ignore_index=-100, reduction='mean', label_smoothing=0.0)
️
size_averageandreduceParameter is deprecated , In its placereductionParameters , So I won't explain it here
With the bedding in front , We can easily understand these parameters :
weight: The length is C C C Tensor , It is generally used when the data is unbalanced ;ignore_index: Index of categories that need to be ignored , The default is − 100 -100 −100, That is not to ignore ;reduction: Decide how to return the loss . bynoneWhen to return to N N N Loss of samples , bymeanWhen to return to N N N The average loss of samples , bysumWhen to return to N N N The sum of the loss of samples . The default ismean;label_smoothing: Decide whether to turn on label smoothing ( Readers who do not understand label smoothing can refer to This article ), Values in [ 0 , 1 ] [0,1] [0,1] Inside . The default is 0 0 0, That is, do not open .
3.1 Input and output
Input is divided into input and target,input Usually it is ( N , C ) (N,C) (N,C) The shape of the ( namely batch_size × num_classes),target Usually it is ( N , ) (N,) (N,) The shape of the , Each of these components is located in [ 0 , C − 1 ] ∩ Z [0,C-1] \cap \mathbb{Z} [0,C−1]∩Z in , Represents the category to which the sample belongs .
inputandtargetIt can also be other types of input , But this article only discusses the most widely used inputinputIt is the original output of neural network ( Not passed Softmax),nn.CrossEntropyLossIt will be automatically applied Softmax
torch.manual_seed(0)
batch_size = 3
num_classes = 5
criterion_1 = nn.CrossEntropyLoss(reduction='none')
criterion_2 = nn.CrossEntropyLoss()
criterion_3 = nn.CrossEntropyLoss(reduction='sum')
inputs = torch.randn(batch_size, num_classes) # Avoid and input Keyword conflict ( Of course, it doesn't matter )
target = torch.randint(num_classes, size=(batch_size, ))
print(criterion_1(inputs, target)) # Output 3 A sample of loss
# tensor([1.4639, 3.0493, 2.3056])
print(criterion_2(inputs, target)) # Output 3 A sample of loss The average of
# tensor(2.2729)
print(criterion_3(inputs, target)) # Output 3 A sample of loss And
# tensor(6.8188)
print(sum(criterion_1(inputs, target)) == criterion_3(inputs, target))
# tensor(True)
print(sum(criterion_1(inputs, target)) / batch_size == criterion_2(inputs, target))
# tensor(True)
Four 、 Start from scratch nn.CrossEntropyLoss
In order to deepen our understanding of , Next, let's start from scratch nn.CrossEntropyLoss( Of course, it will be different from the official , In order to pursue readability, it will be implemented in a fool's way ).
First determine the framework ( For simplicity, we don't consider label_smoothing):
class CrossEntropyLoss(nn.Module):
def __init__(self, weight=None, ignore_index=-100, reduction='mean'):
super().__init__()
self.weight = weight
self.ignore_index = ignore_index
self.reduction = reduction
def forward(self, inputs, target):
pass
For ease of calculation , We rewrite the loss calculation formula in Chapter 2
l n = w y n ⋅ I ( y n ≠ i ) ⋅ [ − x n , y n + log ∑ c = 1 C exp ( x n c ) ] l_n=w_{y_n}\cdot \mathbb{I}(y_n\neq i)\cdot[-x_{n,y_n}+\log\sum_{c=1}^C\exp(x_{nc})] ln=wyn⋅I(yn=i)⋅[−xn,yn+logc=1∑Cexp(xnc)]
Adopt more consistent Python To rewrite the above formula
l n = w [ y n ] ⋅ I ( y n ≠ i ) ⋅ [ − x n [ y n ] + log ∑ c = 1 C exp ( x n [ c ] ) ] l_n=\boldsymbol{w}[y_n]\cdot \mathbb{I}(y_n\neq i)\cdot[-\boldsymbol{x_n}[y_n]+\log\sum_{c=1}^C\exp(\boldsymbol{x_n}[c])] ln=w[yn]⋅I(yn=i)⋅[−xn[yn]+logc=1∑Cexp(xn[c])]
among w = ( w 1 , ⋯ , w C ) , x n = ( x n 1 , ⋯ , x n C ) \boldsymbol{w}=(w_1,\cdots,w_C),\;\boldsymbol{x_n}=(x_{n1},\cdots,x_{nC}) w=(w1,⋯,wC),xn=(xn1,⋯,xnC). Re order X = ( x 1 ; ⋯ ; x N ) , y = ( y 1 , ⋯ , y C ) {\bf X}=(\boldsymbol{x_1};\cdots;\boldsymbol{x_N}),\;\boldsymbol{y}=(y_1,\cdots,y_C) X=(x1;⋯;xN),y=(y1,⋯,yC), Obviously X {\bf X} X It's ours input, y \boldsymbol{y} y Namely target, So we can do batch calculation
( l 1 , ⋯ , l N ) = w [ y ] ∗ I ( y ≠ i ) ∗ ( − X [ range ( len ( y ) ) , y ] + log ( sum ( exp ( X ) , dim = 1 ) ) ) (l_1,\cdots,l_N)=\boldsymbol{w}[\boldsymbol{y}] *\mathbb{I}(\boldsymbol{y}\neq i)* (-{\bf X}[\text{range}(\text{len}(\boldsymbol{y})),\,\boldsymbol{y}]+\log(\text{sum}(\exp({\bf X}),\,\text{dim}=1))) (l1,⋯,lN)=w[y]∗I(y=i)∗(−X[range(len(y)),y]+log(sum(exp(X),dim=1)))
among ∗ * ∗ Means multiply by elements . The above formula adopts the broadcasting mechanism .
class CrossEntropyLoss(nn.Module):
def __init__(self, weight=None, ignore_index=-100, reduction='mean'):
super().__init__()
self.weight = weight
self.ignore_index = ignore_index
self.reduction = reduction
def forward(self, inputs, target):
if self.weight is not None:
n_samples_weight = self.weight[target] # The weight of each sample
else:
n_samples_weight = torch.ones_like(target).float() # If no weight is provided, all are by default 1
indicator = (target != self.ignore_index).long().float() # long() Method can transform Boolean tensor into 0-1 tensor
raw_loss = -inputs[torch.arange(len(target)), target] + torch.log(torch.sum(torch.exp(inputs), dim=1))
result = n_samples_weight * indicator * raw_loss
if self.reduction == 'mean':
return torch.sum(result) / n_samples_weight.dot(indicator)
elif self.reduction == 'sum':
return torch.sum(result)
else:
return result
The output is consistent with PyTorch Official nn.CrossEntropyLoss It's exactly the same , No more here , Readers can verify .
边栏推荐
- Transfer learning and domain adaptation
- Rebuild my 3D world [open source] [serialization-1]
- asp. Net (c)
- 多元线性回归(梯度下降法)
- Beautiful soup parsing and extracting data
- Ros-10 roslaunch summary
- 生成对抗网络
- Rebuild my 3D world [open source] [serialization-3] [comparison between colmap and openmvg]
- MPSoC QSPI Flash 升级办法
- 特征工程
猜你喜欢

嗨 FUN 一夏,与 StarRocks 一起玩转 SQL Planner!
![[code practice] [stereo matching series] Classic ad census: (5) scan line optimization](/img/54/cb1373fbe7b21c5383580e8b638a2c.jpg)
[code practice] [stereo matching series] Classic ad census: (5) scan line optimization
![C [essential skills] use of configurationmanager class (use of file app.config)](/img/8b/e56f87c2d0fbbb1251ec01b99204a1.png)
C [essential skills] use of configurationmanager class (use of file app.config)

Introduction Guide to stereo vision (7): stereo matching
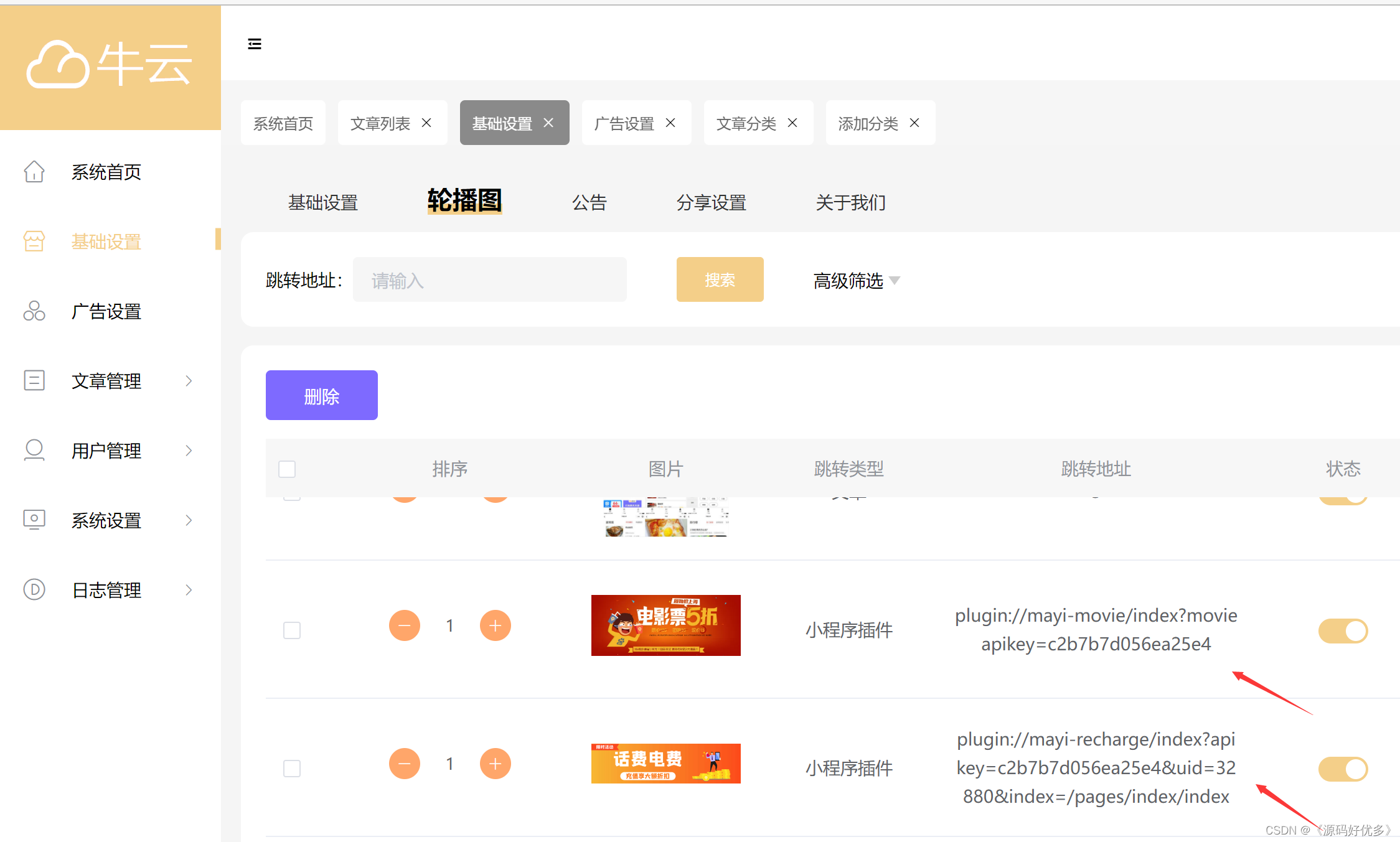
Add discount recharge and discount shadow ticket plug-ins to the resource realization applet

Halcon color recognition_ fuses. hdev:classify fuses by color
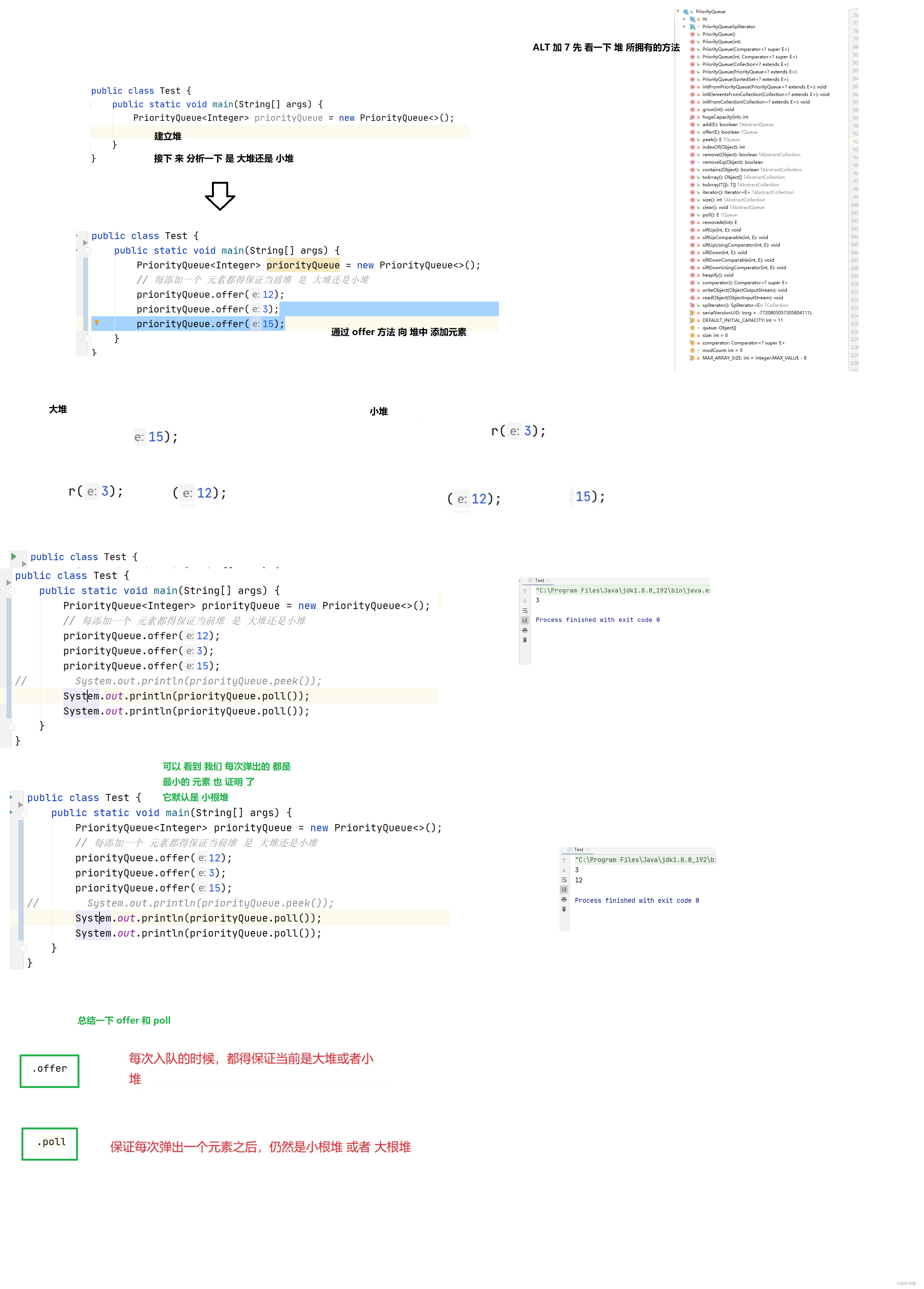
优先级队列(堆)
Attention is all you need
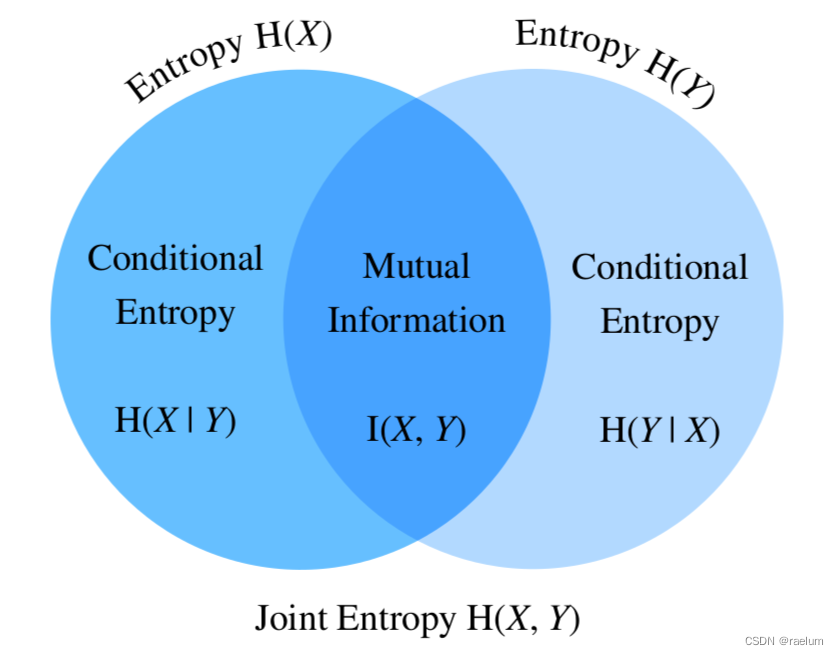
信息與熵,你想知道的都在這裏了

信息与熵,你想知道的都在这里了
随机推荐
某公司文件服务器迁移方案
Golang foundation -- map, array and slice store different types of data
Characteristic Engineering
Codeworks round 639 (Div. 2) cute new problem solution
kubeadm系列-01-preflight究竟有多少check
Halcon snap, get the area and position of coins
asp. Net (c)
Blogger article navigation (classified, real-time update, permanent top)
Redis实现高性能的全文搜索引擎---RediSearch
什么是防火墙?防火墙基础知识讲解
迁移学习和域自适应
[code practice] [stereo matching series] Classic ad census: (4) cross domain cost aggregation
Introduction Guide to stereo vision (7): stereo matching
C [essential skills] use of configurationmanager class (use of file app.config)
Ecmascript6 introduction and environment construction
Nodemon installation and use
2011-11-21 training record personal training (III)
Attention is all you need
Use arm neon operation to improve memory copy speed
Multiple solutions to one problem, asp Net core application startup initialization n schemes [Part 1]