当前位置:网站首页>Realization of binary relation of discrete mathematics with C language and its properties
Realization of binary relation of discrete mathematics with C language and its properties
2022-07-05 07:41:00 【LCH Nan'an】
One 、 The experiment purpose Master the representation of binary relationship on computer , And it can be realized by computer to determine the nature of the relationship . |
Two 、 Experimental content Program to judge whether a binary relationship is equivalent , If it is , Find its quotient set .( You can use C or Python To write ). Equivalence relation : aggregate A The binary relationship on R At the same time, it is reflexive 、 Symmetry and transitivity , said R yes A The equivalence relationship on . |
3、 ... and 、 Program design flow chart ( Or experimental principles )
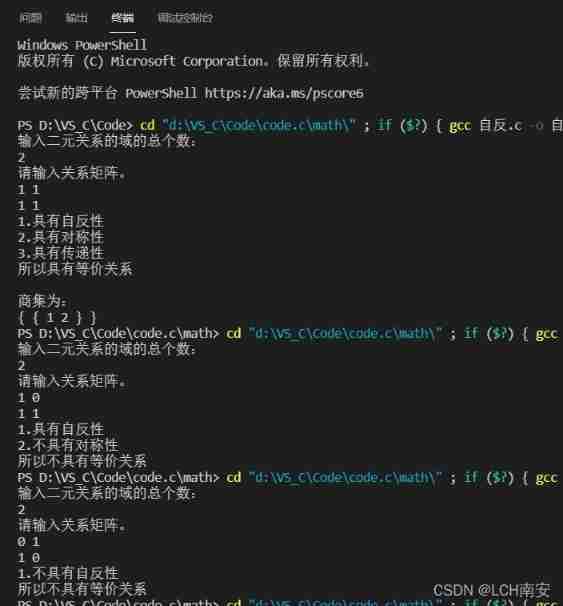
Result chart :
Code : |
边栏推荐
- NSIS search folder
- 使用go语言读取txt文件写入excel中
- Query the table name used by kettle in Oracle
- Line test -- data analysis -- FB -- teacher Gao Zhao
- 2022 PMP project management examination agile knowledge points (7)
- CADD course learning (5) -- Construction of chemosynthesis structure with known target (ChemDraw)
- What is Bezier curve? How to draw third-order Bezier curve with canvas?
- Threads and processes
- [neo4j] common operations of neo4j cypher and py2neo
- Simple operation of nixie tube (keil5)
猜你喜欢
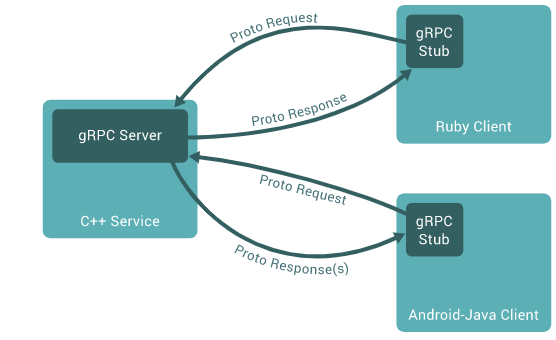
玩转gRPC—深入概念与原理
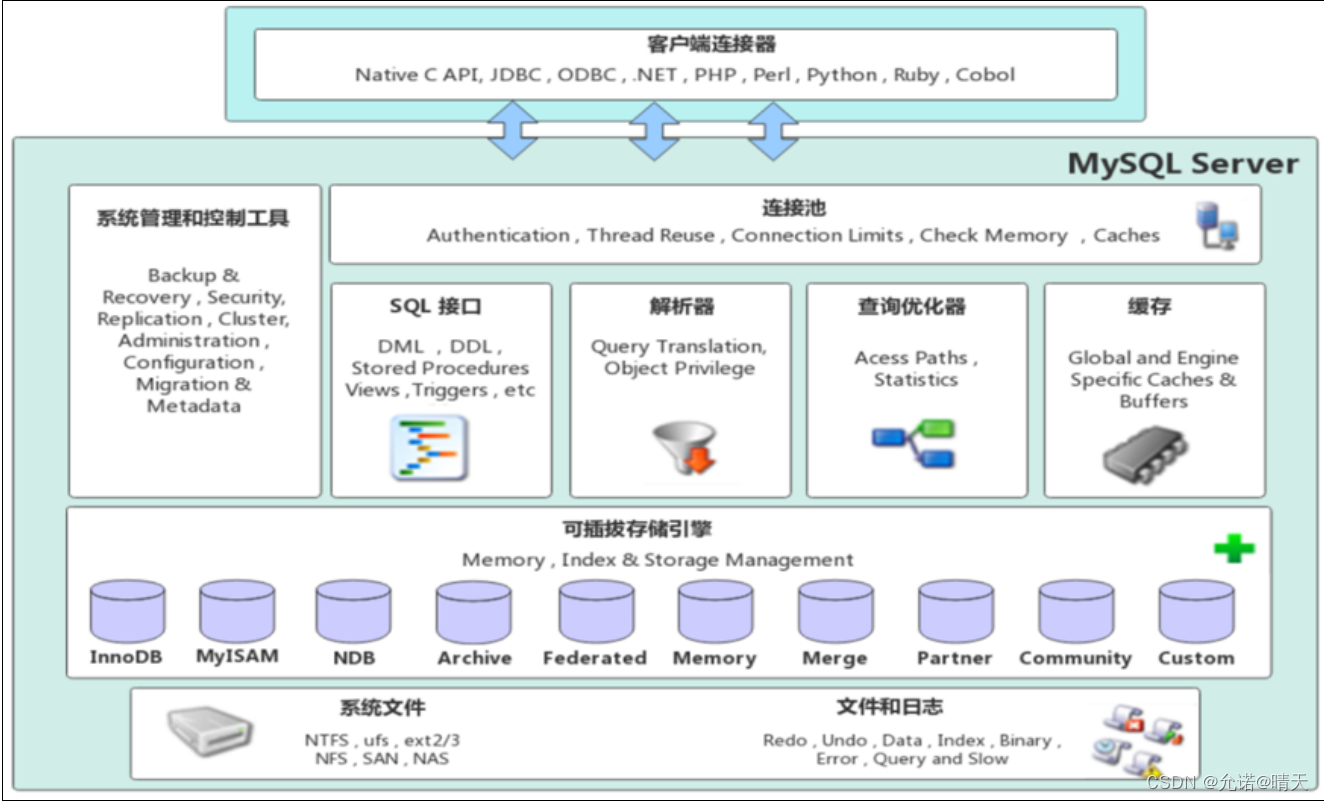
MySql——存储引擎
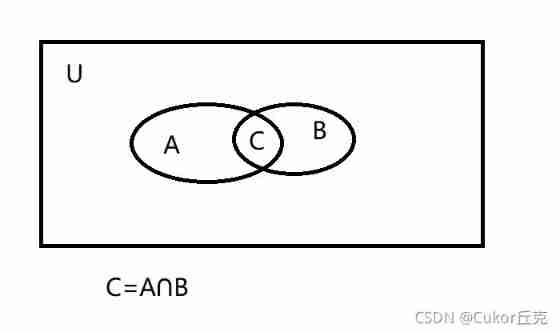
Set theory of Discrete Mathematics (I)
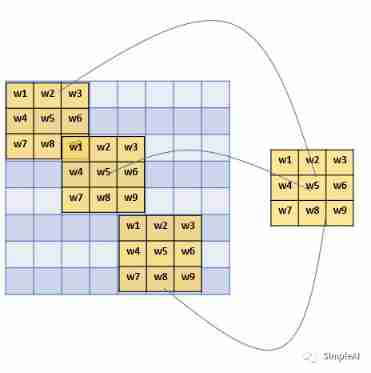
From then on, I understand convolutional neural network (CNN)

Significance and requirements of semiconductor particle control

Daily Practice:Codeforces Round #794 (Div. 2)(A~D)
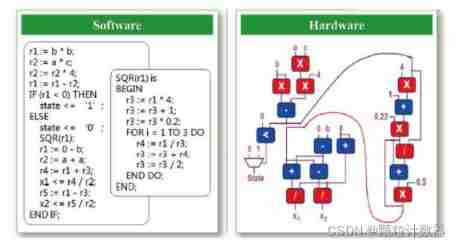
High end electronic chips help upgrade traditional oil particle monitoring
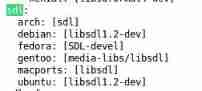
Could NOT find XXX (missing: XXX_LIBRARY XXX_DIR)
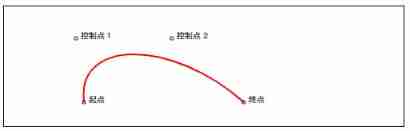
What is Bezier curve? How to draw third-order Bezier curve with canvas?
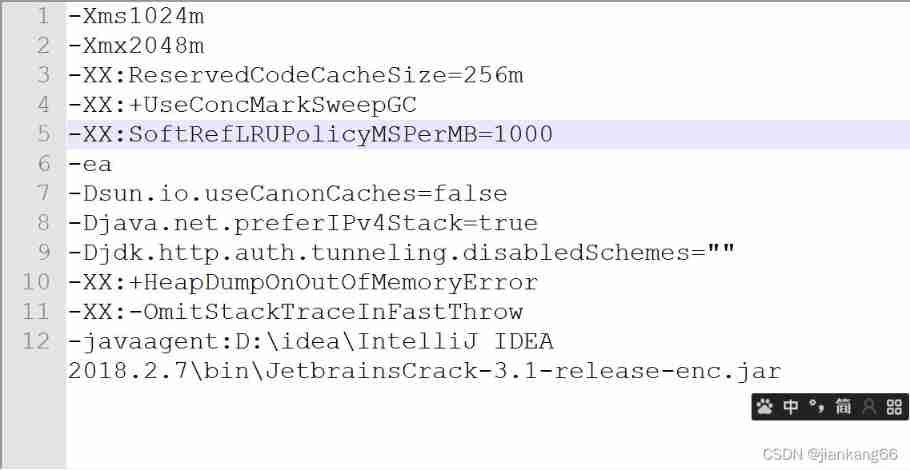
How to deal with excessive memory occupation of idea and Google browser
随机推荐
Detailed explanation of C language pointer
Ugnx12.0 initialization crash, initialization error (-15)
Self summary of college life - freshman
GPIO circuit principle of stm32
[MySQL] database knowledge record
Basic series of SHEL script (II) syntax + operation + judgment
Package ‘*****‘ has no installation candidate
assert_ Usage of param function
Apple system optimization
Rough notes of C language (2) -- constants
CADD course learning (6) -- obtain the existing virtual compound library (drugbank, zinc)
Build your own random wallpaper API for free
Basic series of SHEL script (I) variables
Day01 markdown log entry tips
Numpy——1.数组的创建
Light up the running light, rough notes for beginners (1)
Application of ultra pure water particle counter in electronic semiconductors
MySQL - storage engine
How to deal with excessive memory occupation of idea and Google browser
Rough notes of C language (1)