当前位置:网站首页>POJ - 3616 Milking Time(DP+LIS)
POJ - 3616 Milking Time(DP+LIS)
2022-07-07 08:31:00 【WA_ automata】
POJ - 3616 Milking Time
Description
Bessie is such a hard-working cow. In fact, she is so focused on maximizing her productivity that she decides to schedule her next N (1 ≤ N ≤ 1,000,000) hours (conveniently labeled 0…N-1) so that she produces as much milk as possible.
Farmer John has a list of M (1 ≤ M ≤ 1,000) possibly overlapping intervals in which he is available for milking. Each interval i has a starting hour (0 ≤ starting_houri ≤ N), an ending hour (starting_houri < ending_houri ≤ N), and a corresponding efficiency (1 ≤ efficiencyi ≤ 1,000,000) which indicates how many gallons of milk that he can get out of Bessie in that interval. Farmer John starts and stops milking at the beginning of the starting hour and ending hour, respectively. When being milked, Bessie must be milked through an entire interval.
Even Bessie has her limitations, though. After being milked during any interval, she must rest R (1 ≤ R ≤ N) hours before she can start milking again. Given Farmer Johns list of intervals, determine the maximum amount of milk that Bessie can produce in the N hours.
Input
- Line 1: Three space-separated integers: N, M, and R
- Lines 2…M+1: Line i+1 describes FJ’s ith milking interval withthree space-separated integers: starting_houri , ending_houri , and efficiencyi
Output
- Line 1: The maximum number of gallons of milk that Bessie can product in the N hours
Sample Input
12 4 2
1 2 8
10 12 19
3 6 24
7 10 31
Sample Output
43
The cow is in n Milk production in time , Farmers have m You can milk for a while , Every period of time has a starting point strat, The end point end, And the milking volume during this period w. After each milking , Cows must rest r Time . Ask how much milk you can get under the most reasonable milking arrangement ?
First, sort the interval according to the end time , Then according to the i Whether to choose or not to carry out dynamic planning
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 1010;
struct Node
{
int l,r,val;
}a[N];
int dp[N];
bool cmp(Node A,Node B)
{
return A.r<B.r;
}
int main()
{
int n,m,r;cin>>n>>m>>r;
for(int i=1;i<=m;i++)
{
cin>>a[i].l>>a[i].r>>a[i].val;
a[i].r+=r;
}
sort(a+1,a+m+1,cmp);
for(int i=1;i<=m;i++)
{
dp[i]=a[i].val;
for(int j=1;j<i;j++)
if(a[j].r<=a[i].l)
dp[i]=max(dp[i],dp[j]+a[i].val);
}
int ans=0;
for(int i=1;i<=m;i++)
ans=max(ans,dp[i]);
cout<<ans<<endl;
return 0;
}
边栏推荐
- Pvtv2--pyramid vision transformer V2 learning notes
- 解析机器人科技发展观对社会研究论
- Ebpf cilium practice (2) - underlying network observability
- Ebpf cilium practice (1) - team based network isolation
- The reified keyword in kotlin is used for generics
- Splunk中single value视图使用将数值替换为文字
- 2 - 3 arbre de recherche
- Go语言中,函数是一种类型
- 2-3 lookup tree
- OpenVSCode云端IDE加入Rainbond一体化开发体系
猜你喜欢

National standard gb28181 protocol video platform easygbs adds streaming timeout configuration
Low success rate of unit test report

opencv学习笔记四——膨胀/腐蚀/开运算/闭运算
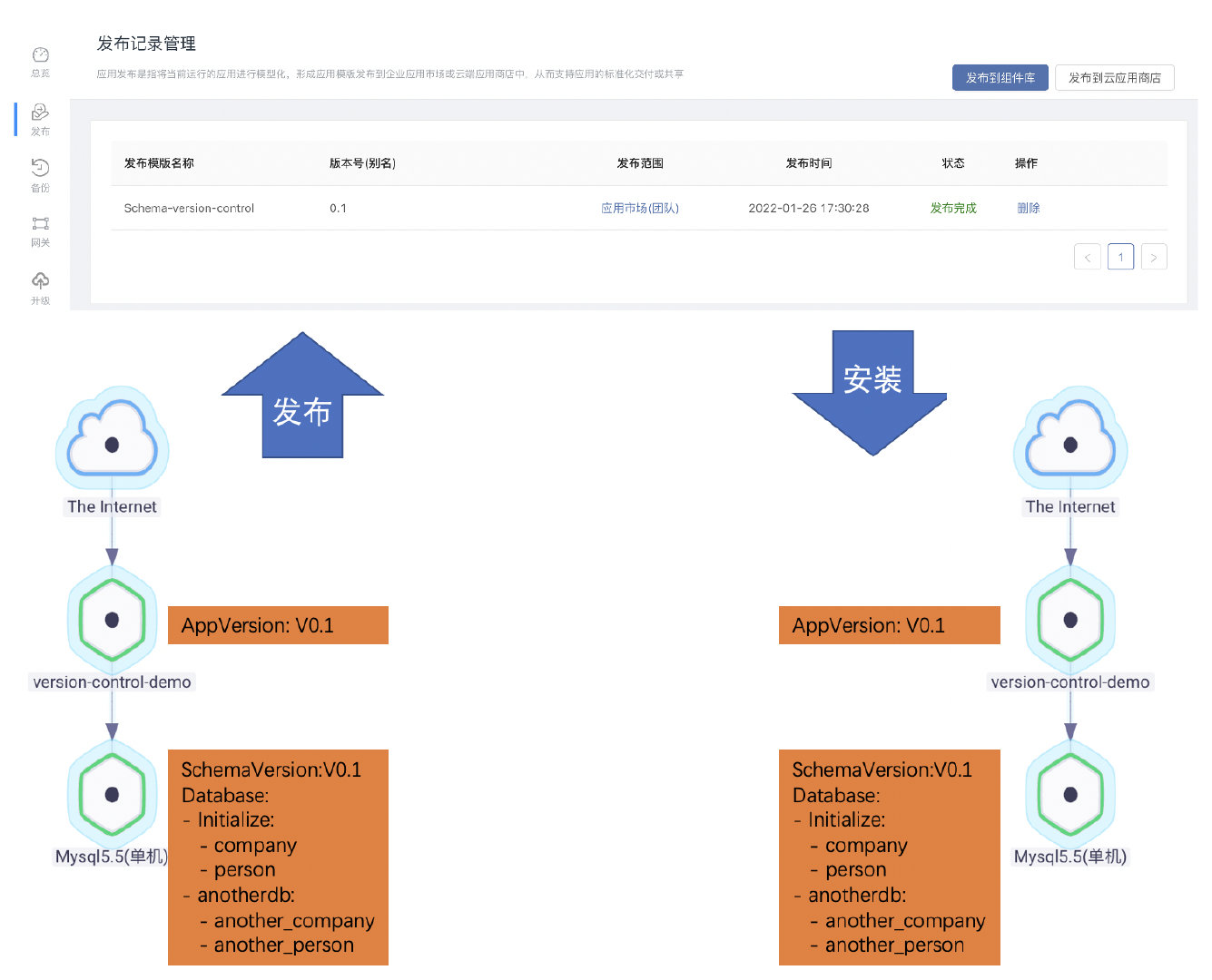
在Rainbond中实现数据库结构自动化升级

Opencv learning note 4 - expansion / corrosion / open operation / close operation

国标GB28181协议视频平台EasyGBS新增拉流超时配置

下载和安装orcale database11.2.0.4

Opencv learning note 3 - image smoothing / denoising
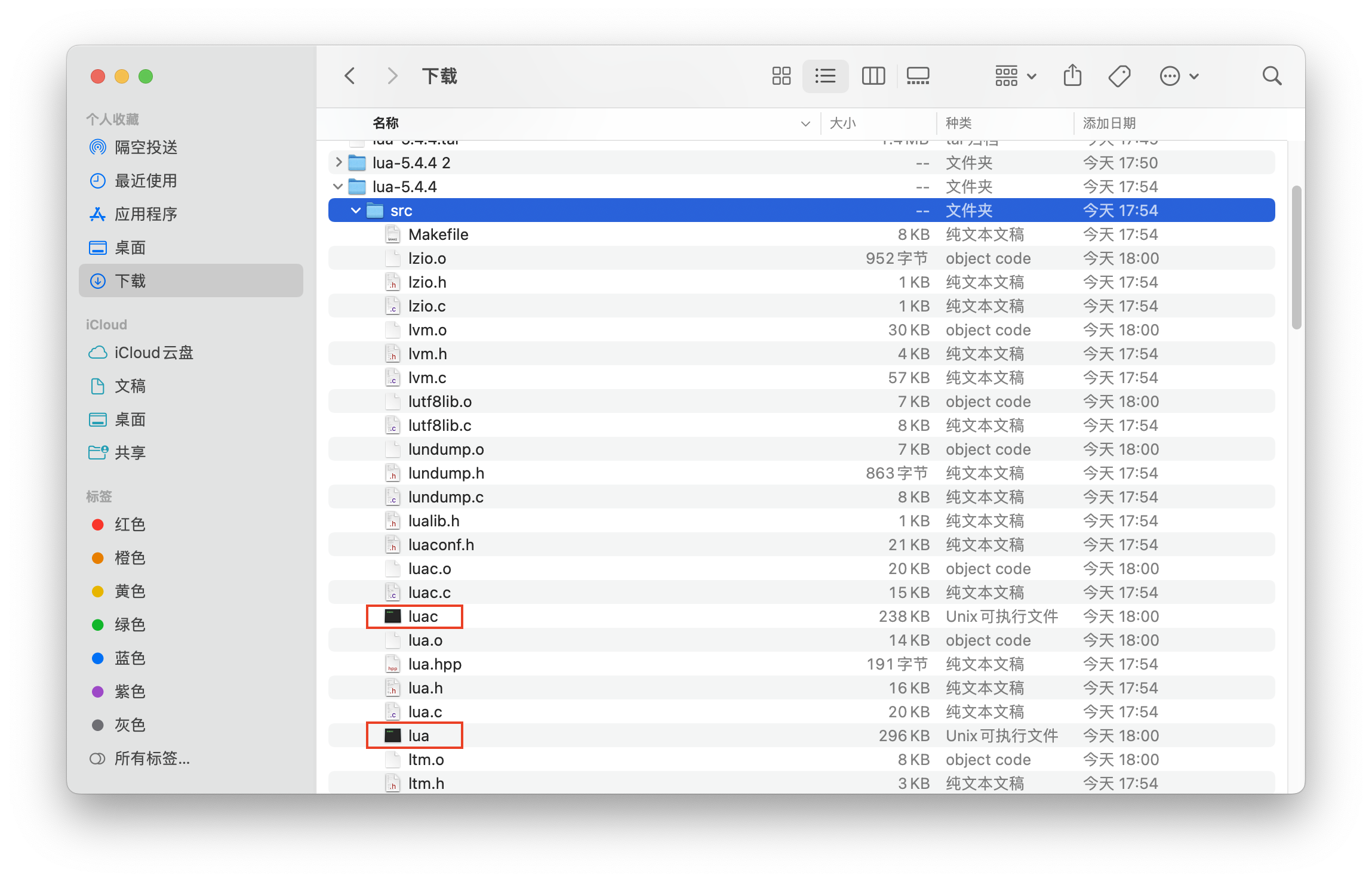
Lua 编程学习笔记
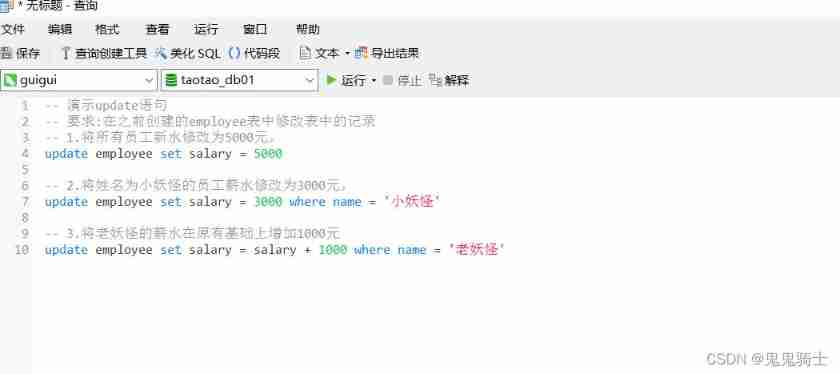
MySQL introduction - crud Foundation (establishment of the prototype of the idea of adding, deleting, changing and searching)
随机推荐
Use of out covariance and in inversion in kotlin
2 - 3 arbre de recherche
【Go ~ 0到1 】 第七天 获取时间戳,时间比较,时间格式转换,Sleep与定时器
Offer harvester: add and sum two long string numbers (classic interview algorithm question)
Réplication de vulnérabilité - désrialisation fastjson
Rainbow 5.7.1 supports docking with multiple public clouds and clusters for abnormal alarms
grpc、oauth2、openssl、双向认证、单向认证等专栏文章目录
打通法律服务群众“最后一公里”,方正璞华劳动人事法律自助咨询服务平台频获“点赞”
Opencv learning notes 1 -- several methods of reading images
Opencv learning note 5 - gradient calculation / edge detection
如何理解分布式架构和微服务架构呢
Domain specific language / DSL in kotlin
Infix keyword infix expression and the use of generic extension function in kotlin
Rsync remote synchronization
【雅思口语】安娜口语学习记录 Part3
[hard core science popularization] working principle of dynamic loop monitoring system
2-3查找樹
Zcmu--1396: queue problem (2)
opencv学习笔记二——图像基本操作
Basic use of CTF web shrink template injection nmap