当前位置:网站首页>快速排序为什么这么快?
快速排序为什么这么快?
2020-11-06 21:04:00 【码农田小齐】


快速排序
首先选一个基准 pivot,然后过一遍数组,
- 把小于 pivot 的都挪到 pivot 的左边,
- 把大于 pivot 的都挪到 pivot 的右边。
这样一来,这个 pivot 的位置就确定了,也就是排好了 1 个元素。
然后对 pivot 左边 的数排序,
对 pivot 右边 的数排序,
就完成了。
那怎么排左边和右边?
答:同样的方法。
所以快排也是用的分治法的思想。
「分」
选择一个 pivot,就把问题分成了
- pivot 左边
- pivot 右边
这两个问题。
「治」
就是最开始描述的方法,直到每个区间内没有元素或者只剩一个元素就可以返回了。
「合」
放在一起自然就是。
但是如何选择这个 pivot?
取中间的?
取第一个?
取最后一个?
举个例子:{5, 2, 1, 0, 3}.
比如选最后一个,就是 3.
然后我们就需要把除了 3 之外的数分成「比 3 大」和「比 3 小」的两部分,这个过程叫做 partition(划分)。
这里我们仍然使用「挡板法」的思想,不用真的弄两个数组来存这两部分,而是用两个挡板,把区间划分好了。
我们用「两个指针」(就是挡板)把数组分成「三个区间」,那么
- 左边的区间用来放小于 pivot 的元素;
- 右边的区间用来放大于 pivot 的元素;
- 中间是未排序区间。

那么初始化时,我们要保证「未排序区间」能够包含除了 3 之外的所有元素,所以
- 未排序区间 = [i, j]
这样左边和右边的区间就成了:
- [0, i):放比 3 小的数;
- (j, array.length -2]:放比 3 大的数
注意 ️ i, j 是不包含在左右区间里的呢。
那我们的目的是 check 未排序区间里的每一个数,然后把它归到正确的区间里,以此来缩小未排序区间,直到没有未排序的元素。
从左到右来 check:
Step1.
5 > 3, 所以 5 要放在右区间里,所以 5 和 j 指向的 0 交换一下:

这样 5 就排好了,指针 j --,这样我们的未排序区间就少了一个数;
Step2.
0 < 3,所以就应该在左边的区间,直接 i++;

Step3.
2 < 3,同理,i++;

Step4.
1 < 3,同理,i++;

所以当两个指针错位的时候,我们结束循环。
但是还差了一步,3 并不在正确的位置上呀。所以还要把它插入到两个区间中间,也就是和指针 i 交换一下。


齐姐声明:这里并不鼓励大家把 pivot 放最左边。
基本所有的书上都是放右边,既然放左右都是一样的,我们就按照大家默认的、达成共识的来,没必要去“标新立异”。
就比如围棋的四个星位,但是讲究棋道的就是先落自己这边的星位,而不是伸着胳膊去够对手那边的。
那当我们把 pivot 换回到正确的位置上来之后,整个 partition 就结束了。
之后就用递归的写法,对左右两边排序就好了。
最后还有两个问题想和大家讨论一下:
- 回到我们最初选择 pivot的问题,每次都取最后一个,这样做好不好?
答:并不好。
因为我们是想把数组分割的更均匀,均匀的时间复杂度更低;但是如果这是一个有序的数组,那么总是取最后一个是最不均匀的取法。
所以应该随机取 pivot,这样就避免了因为数组本身的特点总是取到最值的情况。
- pivot 放在哪
随机选取之后,我们还是要把这个 pivot 放到整个数组的最右边,这样我们的未排序区间才是连续的,否则每次走到 pivot 这里还要想着跳过它,心好累哦。
class Solution {
public void quickSort(int[] array) {
if (array == null || array.length <= 1) {
return;
}
quickSort(array, 0, array.length - 1);
}
private void quickSort(int[] array, int left, int right) {
// base case
if (left >= right) {
return;
}
// partition
Random random = new Random(); // java.util 中的随机数生成器
int pivotIndex = left + random.nextInt(right - left + 1);
swap(array, pivotIndex, right);
int i = left;
int j = right-1;
while (i <= j) {
if (array[i] <= array[right]) {
i++;
} else {
swap(array, i, j);
j--;
}
}
swap(array, i, right);
//「分」
quickSort(array, left, i-1);
quickSort(array, i+1, right);
}
private void swap(int[] array, int x, int y) {
int tmp = array[x];
array[x] = array[y];
array[y] = tmp;
}
}
这里的时空复杂度和分的是否均匀有很大关系,所以我们分情况来说:
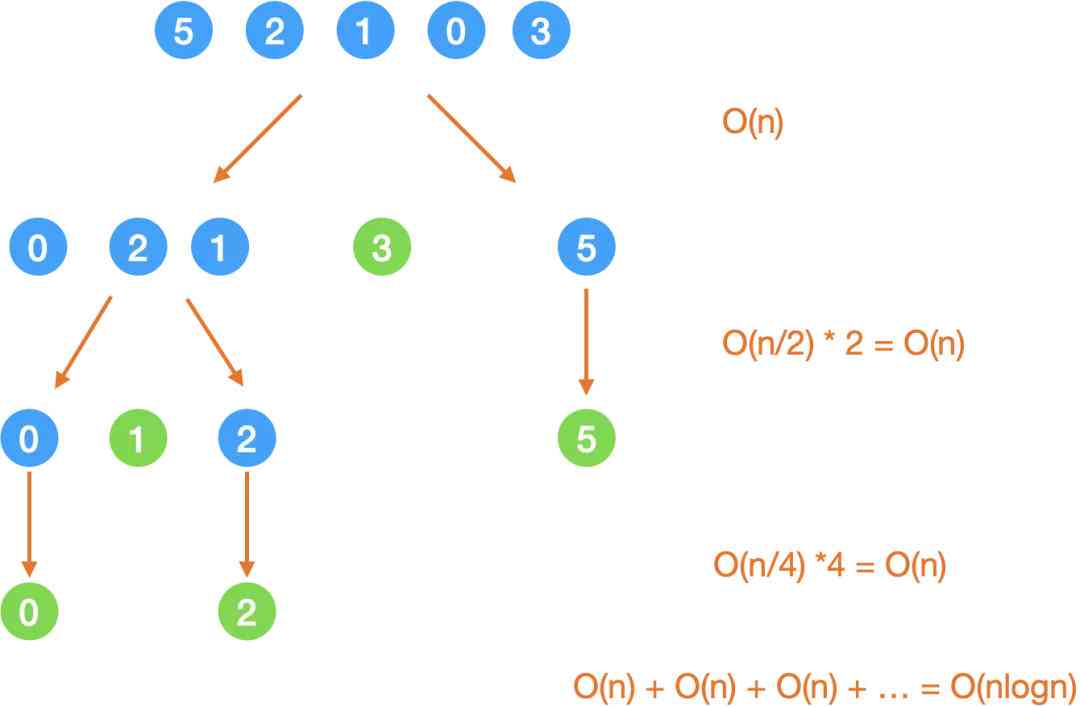
1. 均分
时间复杂度
如果每次都能差不多均匀分,那么
- 每次循环的耗时主要就在这个 while 循环里,也就是 O(right - left);
- 均分的话那就是 logn 层;
- 所以总的时间是 O(nlogn).
空间复杂度
- 递归树的高度是 logn,
- 每层的空间复杂度是 O(1),
- 所以总共的空间复杂度是 O(logn).
2. 最不均匀
如果每次都能取到最大/最小值,那么递归树就变成了这个样子:

时间复杂度
如上图所示:O(n^2)
空间复杂度
这棵递归树的高度就变成了 O(n).
3. 总结
实际呢,大多数情况都会接近于均匀的情况,所以均匀的情况是一个 average case.
为什么看起来最好的情况实际上是一个平均的情况呢?
因为即使如果没有取到最中间的那个点,比如分成了 10% 和 90% 两边的数,那其实每层的时间还是 O(n),只不过层数变成了以 9 为底的 log,那总的时间还是 O(nlogn).
所以快排的平均时间复杂度是 O(nlogn)。
稳定性
那你应该能看出来了,在 swap 的时候,已经破坏了元素之间的相对顺序,所以快排并不具有稳定性。
这也回答了我们开头提出的问题,就是
-
为什么对于 primitive type 使用快排,
- 因为它速度最快;
-
为什么对于 object 使用归并,
- 因为它具有稳定性且快。
以上就是快排的所有内容了,也是很常考的内容哦!那下一篇文章我会讲几道从快排引申出来的题目,猜猜是什么?
如果你喜欢这篇文章,记得给我点赞留言哦~你们的支持和认可,就是我创作的最大动力,我们下篇文章见!
我是小齐,纽约程序媛,终生学习者,每天晚上 9 点,云自习室里不见不散!
更多干货文章见我的 Github: https://github.com/xiaoqi6666/NYCSDE

版权声明
本文为[码农田小齐]所创,转载请带上原文链接,感谢
https://my.oschina.net/u/4612374/blog/4703349
边栏推荐
- React design pattern: in depth understanding of react & Redux principle
- Natural language processing - wrong word recognition (based on Python) kenlm, pycorrector
- 零基础打造一款属于自己的网页搜索引擎
- git rebase的時候捅婁子了,怎麼辦?線上等……
- Lane change detection
- vue-codemirror基本用法:实现搜索功能、代码折叠功能、获取编辑器值及时验证
- The choice of enterprise database is usually decided by the system architect - the newstack
- The difference between Es5 class and ES6 class
- ES6学习笔记(五):轻松了解ES6的内置扩展对象
- vue任意关系组件通信与跨组件监听状态 vue-communication
猜你喜欢

EOS创始人BM: UE,UBI,URI有什么区别?
Not long after graduation, he earned 20000 yuan from private work!

全球疫情加速互联网企业转型,区块链会是解药吗?

Music generation through deep neural network
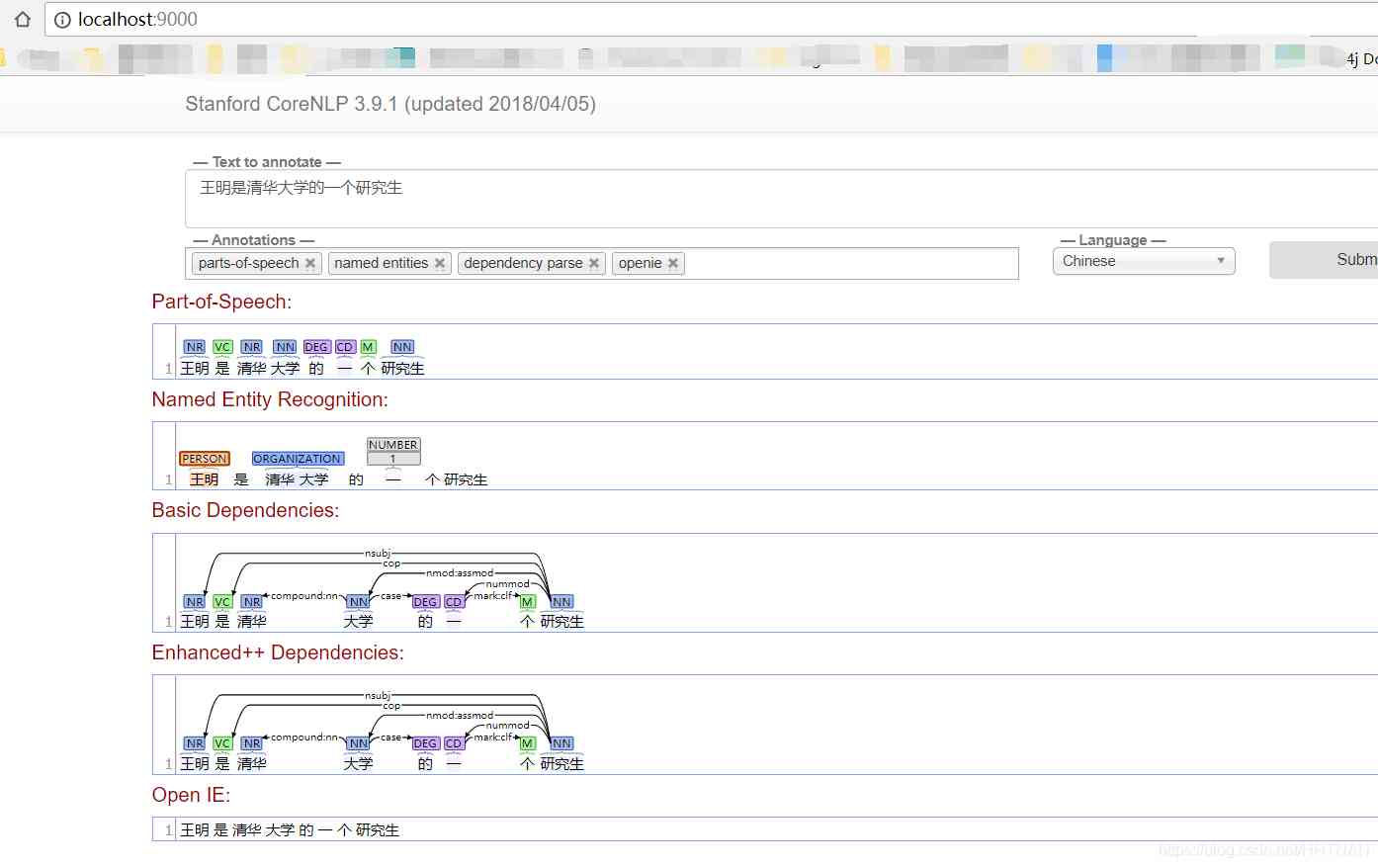
Word segmentation, naming subject recognition, part of speech and grammatical analysis in natural language processing
Character string and memory operation function in C language

合约交易系统开发|智能合约交易平台搭建

Summary of common string algorithms

Elasticsearch数据库 | Elasticsearch-7.5.0应用搭建实战

ES6学习笔记(二):教你玩转类的继承和类的对象
随机推荐
Natural language processing - wrong word recognition (based on Python) kenlm, pycorrector
How to become a data scientist? - kdnuggets
Elasticsearch数据库 | Elasticsearch-7.5.0应用搭建实战
有了这个神器,快速告别垃圾短信邮件
Python + appium automatic operation wechat is enough
If PPT is drawn like this, can the defense of work report be passed?
keras model.compile Loss function and optimizer
ES6学习笔记(五):轻松了解ES6的内置扩展对象
如何玩转sortablejs-vuedraggable实现表单嵌套拖拽功能
6.3 handlerexceptionresolver exception handling (in-depth analysis of SSM and project practice)
Recommendation system based on deep learning
What to do if you are squeezed by old programmers? I don't want to quit
Word segmentation, naming subject recognition, part of speech and grammatical analysis in natural language processing
带你学习ES5中新增的方法
Skywalking series blog 1 - install stand-alone skywalking
How to select the evaluation index of classification model
IPFS/Filecoin合法性:保护个人隐私不被泄露
中小微企业选择共享办公室怎么样?
6.1.1 handlermapping mapping processor (1) (in-depth analysis of SSM and project practice)
Skywalking series blog 5-apm-customize-enhance-plugin