After reading this article , You can go and get the following questions ：
1312. The minimum number of inserts to make a string a palindrome string
-----------
Palindrome strings are the same characters read forward and backward , This kind of problem often appears in written interview .
labuladong The official account has several articles explaining palindrome , Is to judge palindrome string or find the longest palindrome string / Of subsequences ：
Calculate the longest palindrome string
Calculate the longest palindrome subsequence
This paper studies the construction of palindrome string , difficulty Hard Calculate the minimum number of times to insert a string into a palindrome string ：
Enter a string s, You can insert any character anywhere in the string . If you want to put the s It becomes a palindrome string , Please calculate the minimum number of insertions ？
The function signature is as follows ：
int minInsertions(string s);
Like input s = "abcea", The algorithm returns 2, Because you can give s Insert 2 A character becomes a palindrome string "abeceba" perhaps "aebcbea". If input s = "aba", The algorithm returns 0, because s It's already a palindrome string , You don't have to insert any characters .
Thinking analysis
First , To find the minimum number of insertions , That must be exhausting , If we use brute force algorithm to enumerate all the insertion methods , What is the complexity of time ？
You can insert any character between two characters at a time , In addition, judge whether the string is palindrome string , This time complexity is bound to explode , It's exponential .
No doubt about that. , This problem needs to be solved by using dynamic programming techniques . The previous article said , Palindrome problems are generally spread from the middle to both ends of the string , The construction of palindrome strings is similar .
We define a two-dimensional dp Array ,dp[i][j] Is defined as follows ： The string s[i..j], At least it needs to be done dp[i][j] The second insertion can turn into palindrome string .
We want the whole thing s The minimum number of insertions , According to this definition , That is to say, to ask for dp[0][n-1] Size （n by s The length of ）.
meanwhile ,base case It's easy to think of , When i == j when dp[i][j] = 0, Because when i == j when s[i..j] It's just a character , Itself is a palindrome string , So you don't need to do any insertion .
Next is the play of dynamic planning , Using mathematical induction to think about the state transfer equation .
PS： I've seriously written about 100 Multiple original articles , Hand brush 200 Daoli is the subject , All published in labuladong A copy of the algorithm , Continuous updating . Recommended collection , Write the title in the order of my article , Master all kinds of algorithm set, then put into the sea of questions, like fish .
State transition equation
State transition is to deduce the answer to a larger problem from the answer to a small question , from base case To other states . If we want to calculate now dp[i][j] Value , And suppose we've worked out the subproblem dp[i+1][j-1] The value of the , Can you find a way to launch dp[i][j] The value of ？
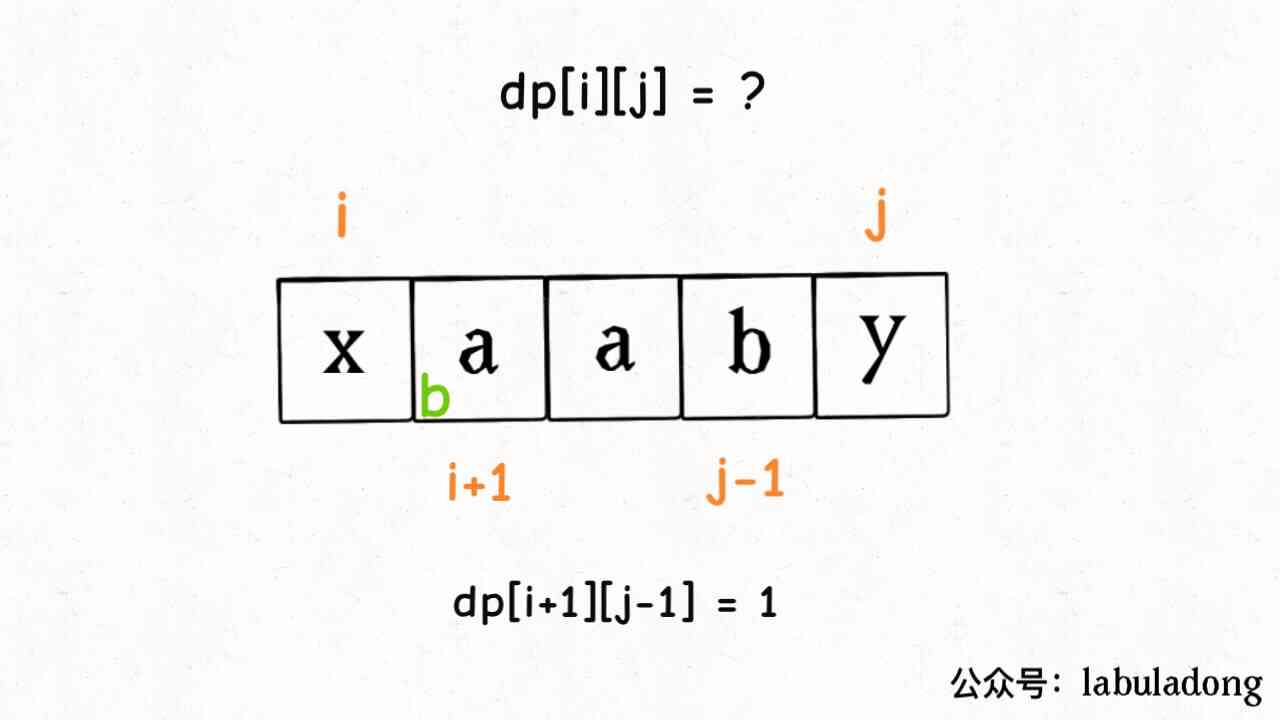
Now that we have worked out dp[i+1][j-1], I know s[i+1..j-1] The minimum number of times to insert palindrome strings , Then we can think that s[i+1..j-1] It's already a palindrome string , So pass dp[i+1][j-1] deduction dp[i][j] The key is s[i] and s[j] These two characters .
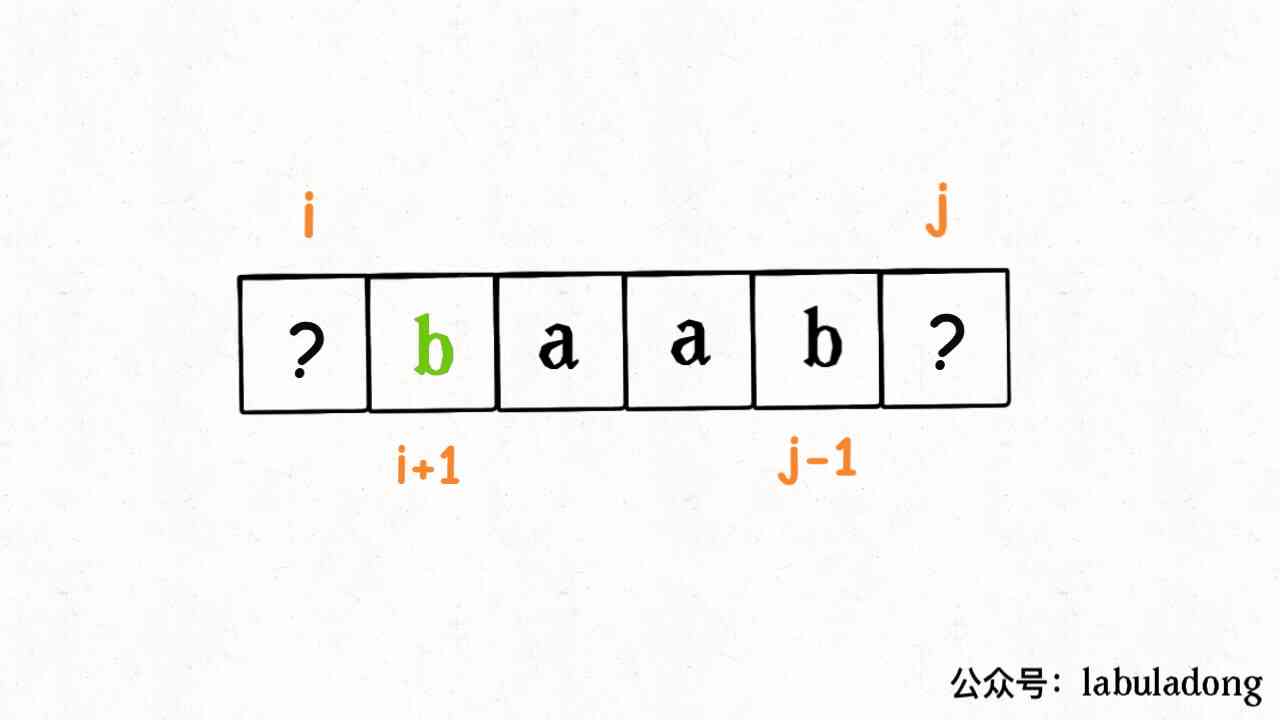
This score situation discussion , If s[i] == s[j] Words , We don't need to do any insertion , Just know how to put s[i+1..j-1] Turn it into a palindrome string ：
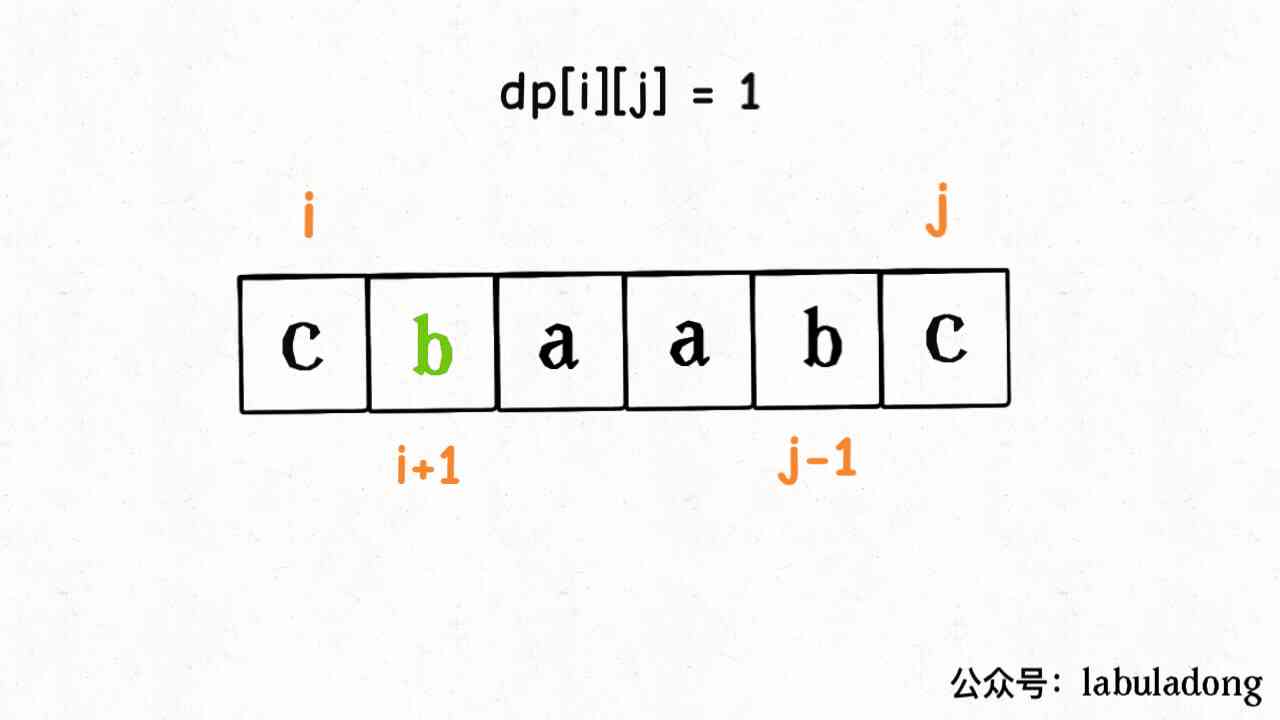
That's how it's translated into code ：
if (s[i] == s[j]) {
dp[i][j] = dp[i + 1][j - 1];
}
If s[i] != s[j] Words , It's a little bit more complicated , For example, the following situation ：
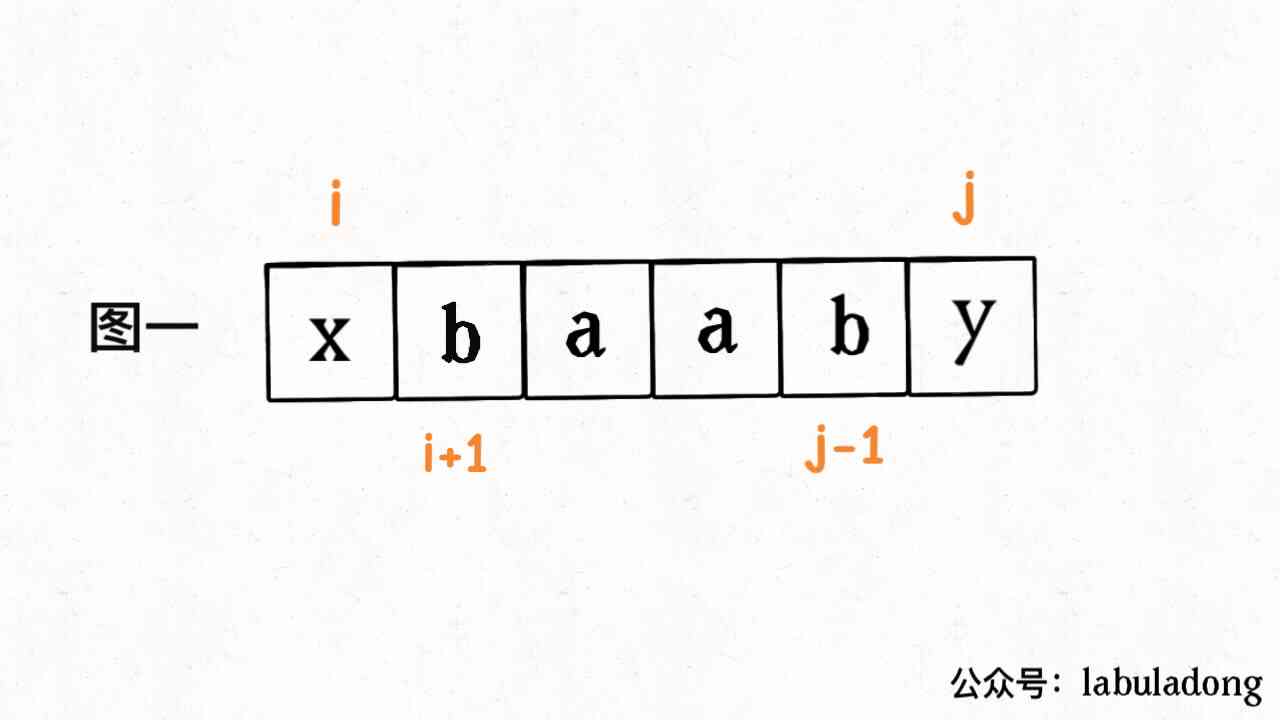
The simplest idea is , The first s[j] insert s[i] On the right , At the same time s[i] insert s[j] On the right , The string constructed in this way must be palindrome string ：
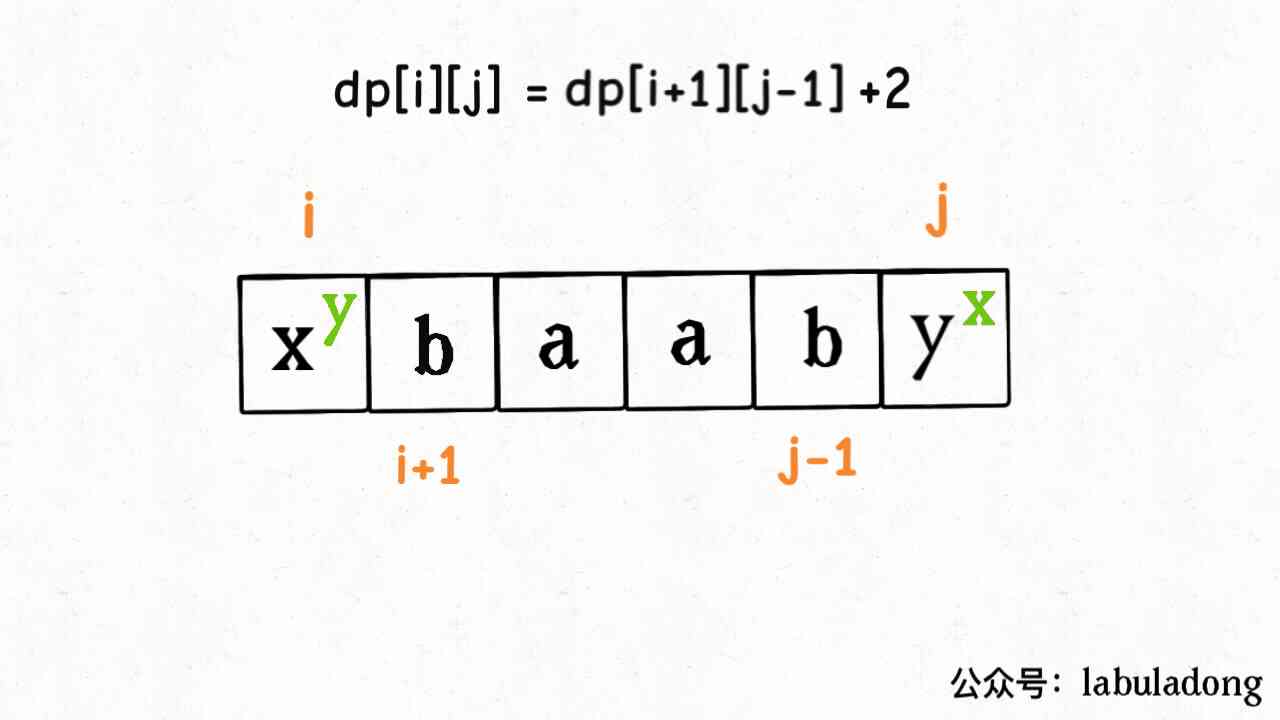
PS： Of course , hold s[j] insert s[i] On the left , And then put s[i] insert s[j] It's the same on the left , We will analyze later .
however , Does this mean that code can be written directly like this ？
if (s[i] != s[j]) {
// hold s[j] insert s[i] On the right , hold s[i] insert s[j] On the right
dp[i][j] = dp[i + 1][j - 1] + 2;
}
incorrect , For example, the following two situations , Just insert a character to make s[i..j] It turns into palindrome ：
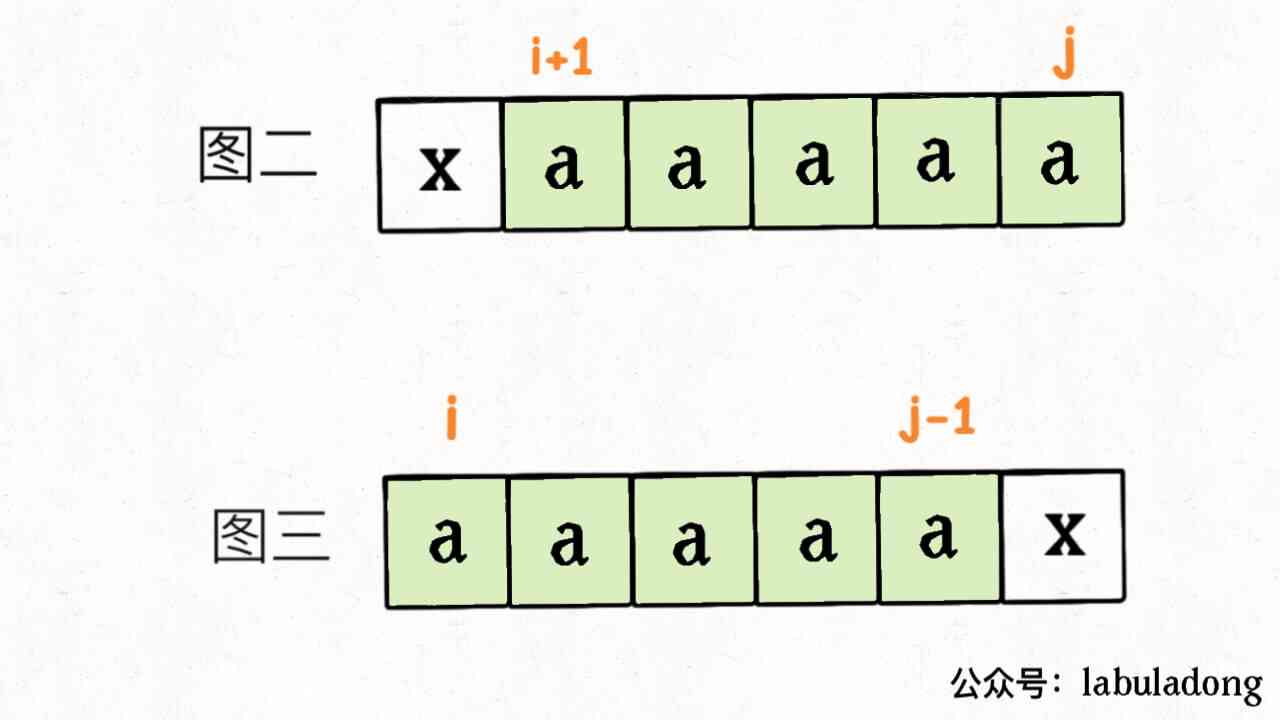
So , When s[i] != s[j] when , Two brain insertions are sure to make s[i..j] It becomes a palindrome string , But not necessarily the least number of inserts , The optimal insertion scheme should be broken down into the following process ：
Step one , To make a choice , First the s[i..j-1] perhaps s[i+1..j] It becomes a palindrome string . How to choose ？ Who becomes palindrome string insert less times , Just choose who you want .
For example, in Figure 2 , take s[i+1..j] The cost of becoming a palindrome string is small , Because it is itself a palindrome string , There's no need to insert ; Empathy , For Figure 3 , take s[i..j-1] It costs less to become palindrome strings .
However , If s[i+1..j] and s[i..j-1] None of them are palindrome strings , You need to insert at least one character to become palindrome , So choose which one is the same ：
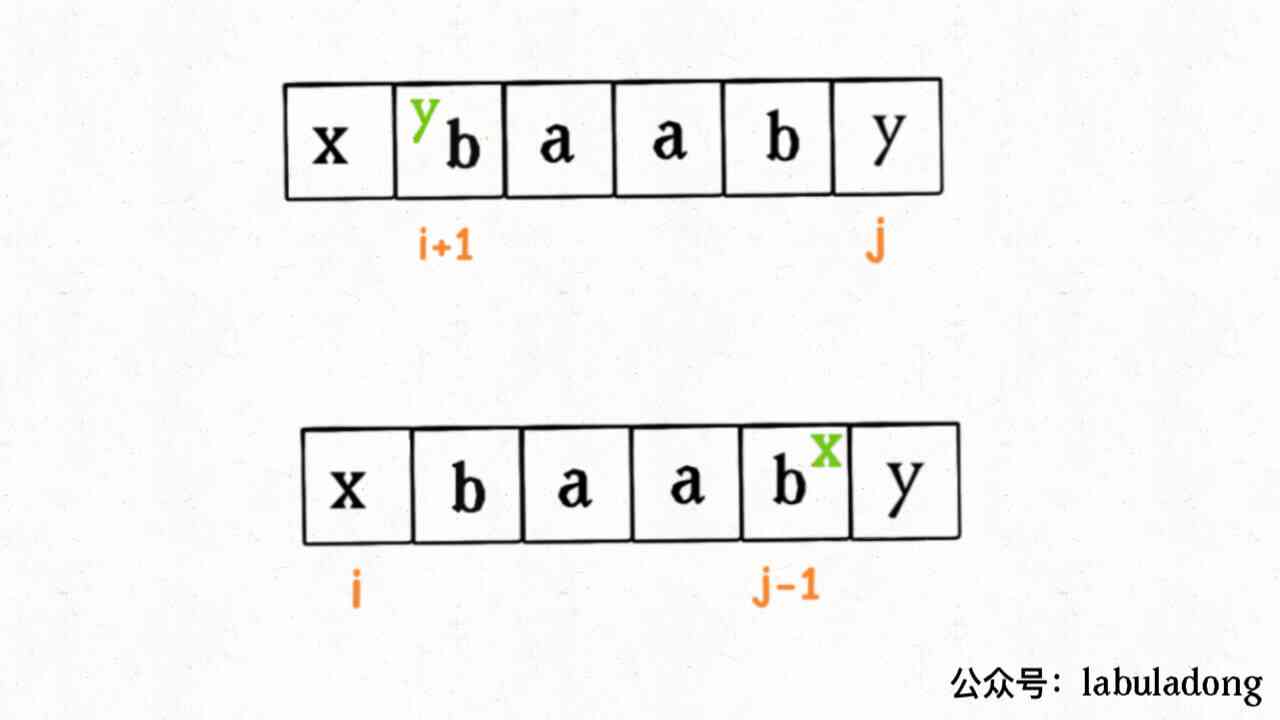
How do I know s[i+1..j] and s[i..j-1] Who is cheaper to become a palindrome string ？
Look back dp What is the definition of an array ,dp[i+1][j] and dp[i][j-1] Isn't it the price of palindrome strings ？
Step two , According to the choice in step one , take s[i..j] It turns into palindrome .
If you choose to put s[i+1..j] It becomes a palindrome string , So in s[i+1..j] Insert a character to the right s[i] It's certain that s[i..j] It turns into palindrome ; Empathy , If you choose to put s[i..j-1] It becomes a palindrome string , stay s[i..j-1] Insert a character to the left s[j] It's certain that s[i..j] It turns into palindrome .
So according to what I just said dp The definition of array and the above analysis ,s[i] != s[j] The code logic is as follows ：
if (s[i] != s[j]) {
// Step one is to choose the less expensive
// Step two must be inserted once
dp[i][j] = min(dp[i + 1][j], dp[i][j - 1]) + 1;
}
combined , The equation of state transfer is as follows ：
if (s[i] == s[j]) {
dp[i][j] = dp[i + 1][j - 1];
} else {
dp[i][j] = min(dp[i + 1][j], dp[i][j - 1]) + 1;
}
This is the core of dynamic programming algorithm , We can write the solution code directly .
PS： I've seriously written about 100 Multiple original articles , Hand brush 200 Daoli is the subject , All published in labuladong A copy of the algorithm , Continuous updating . Recommended collection , Write the title in the order of my article , Master all kinds of algorithm set, then put into the sea of questions, like fish .
Code implementation
First of all to think about base case What is it? , When i == j when dp[i][j] = 0, Because at this time s[i..j] It's a single character , Itself is a palindrome string , No need to insert ; The final answer is dp[0][n-1]（n Is string s The length of ）. that dp table Long like this ：
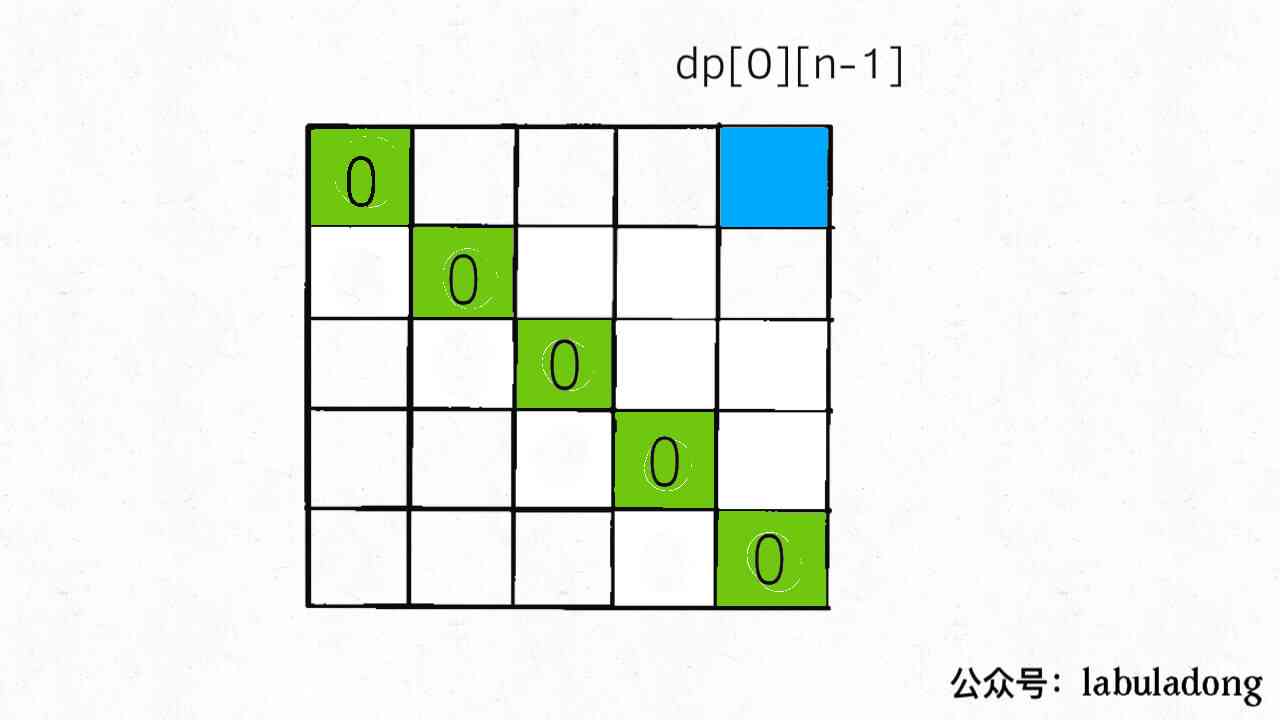
And because in the state transfer equation dp[i][j] and dp[i+1][j],dp[i]-1],dp[i+1][j-1] Three states are related to , To ensure that every calculation dp[i][j] when , All three states have been calculated , We generally choose from the bottom up , Traverse from left to right dp Array ：
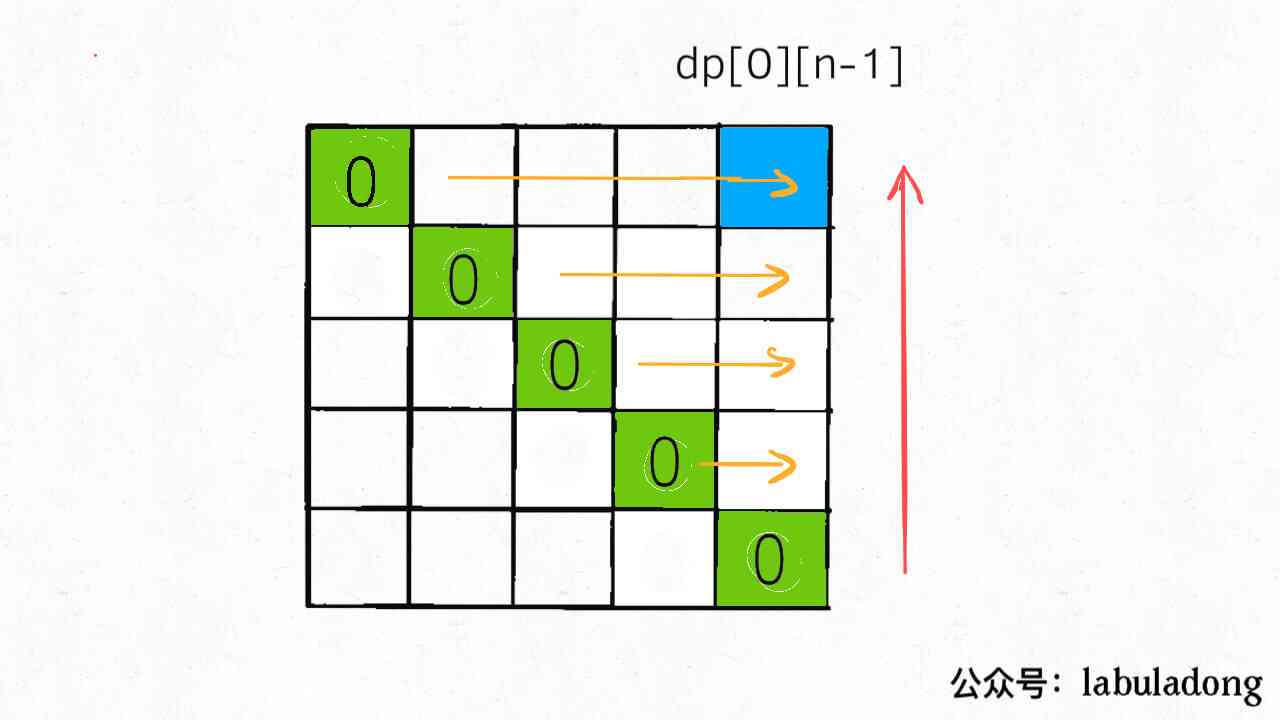
The complete code is as follows ：
int minInsertions(string s) {
int n = s.size();
// Definition ： Yes s[i..j], At least you need to insert dp[i][j] Time can become palindrome
vector<vector<int>> dp(n, vector<int>(n, 0));
// base case：i == j when dp[i][j] = 0, A single character is itself a palindrome
// dp The array has all been initialized to 0,base case Initialized
// Traverse from bottom to top
for (int i = n - 2; i >= 0; i--) {
// Traverse left to right
for (int j = i + 1; j < n; j++) {
// according to s[i] and s[j] Make a state transition
if (s[i] == s[j]) {
dp[i][j] = dp[i + 1][j - 1];
} else {
dp[i][j] = min(dp[i + 1][j], dp[i][j - 1]) + 1;
}
}
}
// according to dp Definition of array , The answer to the question is
return dp[0][n - 1];
}
Now the problem is solved , The complexity of time and space is O(N^2). There's also a small optimization , be aware dp The state of an array is related to its adjacent state , therefore dp Arrays can be compressed into one dimension ：
int minInsertions(string s) {
int n = s.size();
vector<int> dp(n, 0);
int temp = 0;
for (int i = n - 2; i >= 0; i--) {
// Record dp[i+1][j-1]
int pre = 0;
for (int j = i + 1; j < n; j++) {
temp = dp[j];
if (s[i] == s[j]) {
// dp[i][j] = dp[i+1][j-1];
dp[j] = pre;
} else {
// dp[i][j] = min(dp[i+1][j], dp[i][j-1]) + 1;
dp[j] = =min(dp[j], dp[j - 1]) + 1;
}
pre = temp;
}
}
return dp[n - 1];
}
As for how this state compression works , We said earlier State compression techniques I have described in detail , It's not going to unfold here .
＿＿＿＿＿＿＿＿＿＿＿＿＿
my Online e-books Yes 100 Original articles , Hands with brushes 200 Daoli is the subject , Recommended collection ！ Corresponding GitHub Algorithm Repository We've got it 70k star, Welcome to mark star ！
