当前位置:网站首页>【leetcode】1020. Number of enclaves
【leetcode】1020. Number of enclaves
2022-07-07 07:21:00 【Chinese fir sauce_】
subject :
- The number of enclaves
Give you a size of m x n The binary matrix of grid , among 0 Represents an ocean cell 、1 Represents a land cell .
once Move It refers to walking from one land cell to another ( On 、 Next 、 Left 、 Right ) Land cells or across grid The boundary of the .
Return to grid unable The number of land cells that leave the grid boundary in any number of moves .
Example 1: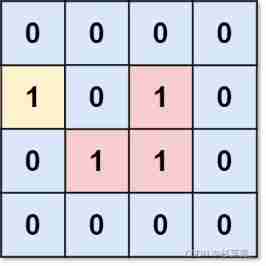
Input :grid = [[0,0,0,0],[1,0,1,0],[0,1,1,0],[0,0,0,0]]
Output :3
explain : There are three 1 By 0 Surround . One 1 Not surrounded , Because it's on the border .
Example 2: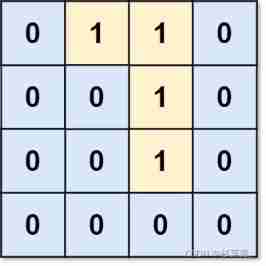
Input :grid = [[0,1,1,0],[0,0,1,0],[0,0,1,0],[0,0,0,0]]
Output :0
explain : all 1 Are on the boundary or can reach the boundary .
Tips :
m == grid.length
n == grid[i].length
1 <= m, n <= 500
grid[i][j] The value of is 0 or 1
Method 1 : Depth-first search
Ideas :
Definition of enclave : If a land cell starts, it cannot move to the grid boundary , Then this land cell is an enclave .
So we can divide all land cells into two categories : The first type of land cells are connected to the network boundary , These land cells are not enclaves ; The second type of land cells are not connected to the grid , These land cells are enclaves .
We can start the depth first search from each land cell on the network boundary , After traversing the boundary , All land cells connected to the grid boundary are accessed . Then traverse the entire grid , If a land cell in the grid has not been accessed , Then the land cell is not connected to the boundary of the grid , It's an enclave .
And because the cells on the grid boundary must not be enclaves , So when traversing the grid and counting the number of enclaves , Just traverse the cells that are not on the grid boundary .
class Solution {
public static int[][] dirs = {
{
-1, 0}, {
1, 0}, {
0, -1}, {
0, 1}};
private int m, n;
private boolean[][] visited;
public int numEnclaves(int[][] grid) {
m = grid.length;
n = grid[0].length;
visited = new boolean[m][n];
for (int i = 0; i < m; i++) {
dfs(grid, i, 0);
dfs(grid, i, n - 1);
}
for (int j = 1; j < n - 1; j++) {
dfs(grid, 0, j);
dfs(grid, m - 1, j);
}
int enclaves = 0;
for (int i = 1; i < m - 1; i++) {
for (int j = 1; j < n - 1; j++) {
if (grid[i][j] == 1 && !visited[i][j]) {
enclaves++;
}
}
}
return enclaves;
}
public void dfs(int[][] grid, int row, int col) {
if (row < 0 || row >= m || col < 0 || col >= n || grid[row][col] == 0 || visited[row][col]) {
return;
}
visited[row][col] = true;
for (int[] dir : dirs) {
dfs(grid, row + dir[0], col + dir[1]);
}
}
}
Complexity analysis :
- Time complexity :O(mn),m and n Grid grid The number of rows and columns . Depth first search accesses each cell at most once , need O(mn) Time for , Traversing the grid to count the number of enclaves also needs O(mn) Time for .
- Spatial complexity :O(mn), among m and n Grid grid The number of rows and columns . The spatial complexity mainly depends on visited Array and recursive call stack space , The space complexity is O(mn).
Method 2 : Breadth first search
You can also judge whether each land cell is connected to the grid boundary by breadth first search .
First, start breadth first search from each land cell on the grid boundary , Access all land cells connected to the boundary , Then traverse the entire grid , Count the number of enclaves .
class Solution {
public static int[][] dirs = {
{
-1, 0}, {
1, 0}, {
0, -1}, {
0, 1}};
public int numEnclaves(int[][] grid) {
int m = grid.length, n = grid[0].length;
boolean[][] visited = new boolean[m][n];
Queue<int[]> queue = new ArrayDeque<int[]>();
for (int i = 0; i < m; i++) {
if (grid[i][0] == 1) {
visited[i][0] = true;
queue.offer(new int[]{
i, 0});
}
if (grid[i][n - 1] == 1) {
visited[i][n - 1] = true;
queue.offer(new int[]{
i, n - 1});
}
}
for (int j = 1; j < n - 1; j++) {
if (grid[0][j] == 1) {
visited[0][j] = true;
queue.offer(new int[]{
0, j});
}
if (grid[m - 1][j] == 1) {
visited[m - 1][j] = true;
queue.offer(new int[]{
m - 1, j});
}
}
while (!queue.isEmpty()) {
int[] cell = queue.poll();
int currRow = cell[0], currCol = cell[1];
for (int[] dir : dirs) {
int nextRow = currRow + dir[0], nextCol = currCol + dir[1];
if (nextRow >= 0 && nextRow < m && nextCol >= 0 && nextCol < n && grid[nextRow][nextCol] == 1 && !visited[nextRow][nextCol]) {
visited[nextRow][nextCol] = true;
queue.offer(new int[]{
nextRow, nextCol});
}
}
}
int enclaves = 0;
for (int i = 1; i < m - 1; i++) {
for (int j = 1; j < n - 1; j++) {
if (grid[i][j] == 1 && !visited[i][j]) {
enclaves++;
}
}
}
return enclaves;
}
}
Complexity analysis :
- Time complexity analysis :O(mn), among m and n Namely grid The number of rows and columns . Breadth first search accesses each cell at most once , need O(mn) Time for , Traversing the grid to count the number of enclaves also needs O(mn) Time for .
- Spatial complexity :O(mn), among m and n Grid grid The number of rows and columns . The spatial complexity mainly depends on visited Array and queue space , The space complexity is O(mn).
Method 3 : Union checking set
In addition to depth first search and breadth first search , You can also use and look up sets to determine whether each land cell is connected to the grid boundary .
The core idea of joint search is to calculate the connected component of each land cell in the grid . For each land cell on the grid boundary , All land cells in the connected component are not enclaves . If the connected component of a land cell is different from the connected component of a land cell on any grid boundary , Then the land cell is an enclave .
The way to search sets is , Traverse the entire grid , For each land cell in the grid , Merge it with all adjacent land cells . Because it is necessary to judge whether the connected component of each land cell is connected with the grid boundary , The information that each cell is connected to the grid boundary is also recorded in the one-time joint search , Update this information during the merge operation .
After traversing the grid and completing the merge operation of search set , Traverse the entire mesh again , Judge whether each land cell is connected with the grid boundary by checking the information in the set , Count the number of enclaves .
class Solution {
public int numEnclaves(int[][] grid) {
int m = grid.length, n = grid[0].length;
UnionFind uf = new UnionFind(grid);
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (grid[i][j] == 1) {
int index = i * n + j;
if (j + 1 < n && grid[i][j + 1] == 1) {
uf.union(index, index + 1);
}
if (i + 1 < m && grid[i + 1][j] == 1) {
uf.union(index, index + n);
}
}
}
}
int enclaves = 0;
for (int i = 1; i < m - 1; i++) {
for (int j = 1; j < n - 1; j++) {
if (grid[i][j] == 1 && !uf.isOnEdge(i * n + j)) {
enclaves++;
}
}
}
return enclaves;
}
}
class UnionFind {
private int[] parent;
private boolean[] onEdge;
private int[] rank;
public UnionFind(int[][] grid) {
int m = grid.length, n = grid[0].length;
parent = new int[m * n];
onEdge = new boolean[m * n];
rank = new int[m * n];
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (grid[i][j] == 1) {
int index = i * n + j;
parent[index] = index;
if (i == 0 || i == m - 1 || j == 0 || j == n - 1) {
onEdge[index] = true;
}
}
}
}
}
public int find(int i) {
if (parent[i] != i) {
parent[i] = find(parent[i]);
}
return parent[i];
}
public void union(int x, int y) {
int rootx = find(x);
int rooty = find(y);
if (rootx != rooty) {
if (rank[rootx] > rank[rooty]) {
parent[rooty] = rootx;
onEdge[rootx] |= onEdge[rooty];
} else if (rank[rootx] < rank[rooty]) {
parent[rootx] = rooty;
onEdge[rooty] |= onEdge[rootx];
} else {
parent[rooty] = rootx;
onEdge[rootx] |= onEdge[rooty];
rank[rootx]++;
}
}
}
public boolean isOnEdge(int i) {
return onEdge[find(i)];
}
}
Complexity analysis :
- Time complexity :O(mn x α(mn)), among m and n Respectively, in the grid grid The number of rows and columns ,α Is the inverse Ackerman function . The join search set here uses path compression and rank merging , The time complexity of a single operation is O(α(mn)), Therefore, the time complexity of the set merging operation of the whole grid is O(mn x α(mn)), After the set search operation, you need O(mn x α(mn)) Time to traverse the grid again and count the number of enclaves , So the total time complexity is O(mn x α(mn)).
- Spatial complexity :O(mn), among m and n Grid grid The number of rows and columns . And search the set needs O(mn) Space .
边栏推荐
- Fast quantitative, abbkine protein quantitative kit BCA method is coming!
- How to model and simulate the target robot [mathematical / control significance]
- Hidden Markov model (HMM) learning notes
- AVL树的实现
- Cloud backup project
- 【JDBC以及内部类的讲解】
- Databinding exception of kotlin
- JS small exercise ---- time sharing reminder and greeting, form password display hidden effect, text box focus event, closing advertisement
- FPGA course: application scenario of jesd204b (dry goods sharing)
- [Luogu p1971] rabbit and egg game (bipartite game)
猜你喜欢

How can brand e-commerce grow against the trend? See the future here!
子组件传递给父组件
Fast quantitative, abbkine protein quantitative kit BCA method is coming!
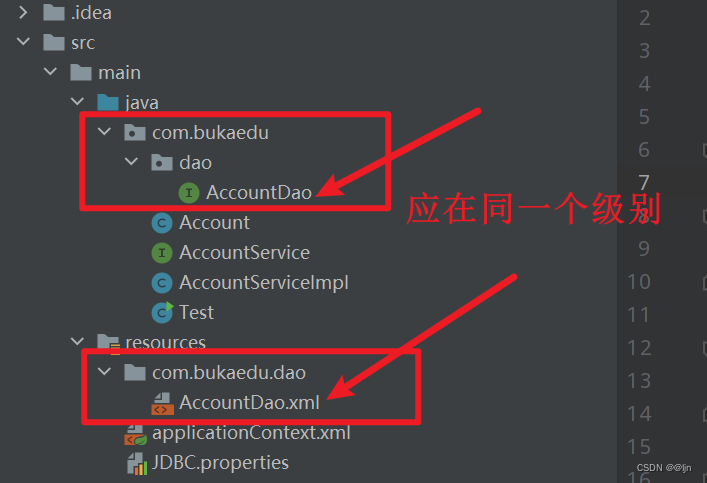
Bindingexception exception (error reporting) processing
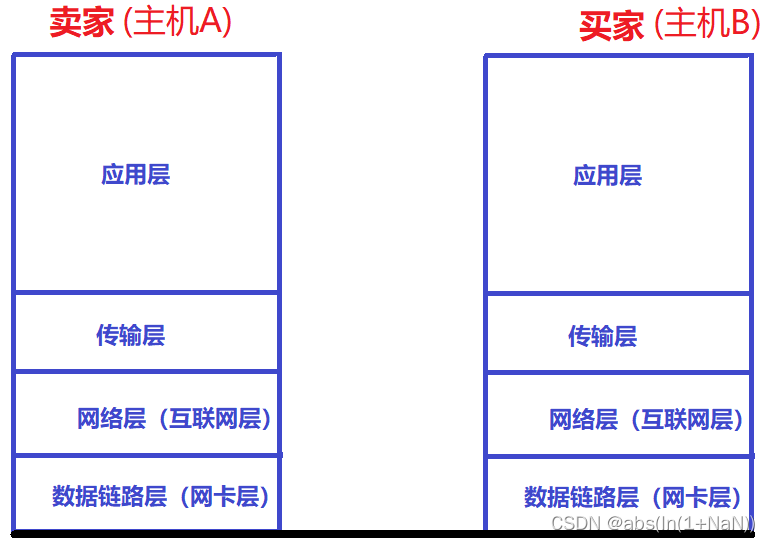
Basic process of network transmission using tcp/ip four layer model
Abnova immunohistochemical service solution
At the age of 20, I got the ByteDance offer on four sides, and I still can't believe it

. Net core accesses uncommon static file types (MIME types)
Implementation of AVL tree
弹性布局(一)
随机推荐
Communication of components
弹性布局(二)
Pass parent component to child component: props
Multidisciplinary integration
How does an enterprise manage data? Share the experience summary of four aspects of data governance
Please ask a question, flick Oracle CDC, read a table without update operation, and repeatedly read the full amount of data every ten seconds
JS decorator @decorator learning notes
Modify the jupyter notebook file path
Role of virtual machine
Exception of DB2 getting table information: caused by: com ibm. db2.jcc. am. SqlException: [jcc][t4][1065][12306][4.25.13]
SQLMAP使用教程(四)实战技巧三之绕过防火墙
Differences between H5 architecture and native architecture
云备份项目
Esxi attaching mobile (Mechanical) hard disk detailed tutorial
LC 面试题 02.07. 链表相交 & LC142. 环形链表II
Bindingexception exception (error reporting) processing
Use of completable future
At the age of 20, I got the ByteDance offer on four sides, and I still can't believe it
計算機服務中缺失MySQL服務
Select the product attribute pop-up box to pop up the animation effect from the bottom