当前位置:网站首页>Chinese remainder theorem acwing 204 Strange way of expressing integers
Chinese remainder theorem acwing 204 Strange way of expressing integers
2022-07-05 06:24:00 【T_ Y_ F666】
Chinese remainder theorem AcWing 204. Strange way to express integers
Original link
AcWing 204. Strange way to express integers
Algorithm tags
Math knowledge Congruence equation Expand the Chinese Remainder Theorem
Ideas




The picture is extracted from the solution of the question
Code
#include<bits/stdc++.h>
#define int long long
#define abs fabs
#define rep(i, a, b) for(int i=a;i<b;++i)
#define Rep(i, a, b) for(int i=a;i>=b;--i)
using namespace std;
const int N = 105;
int a[N][N], eps = 1e-8;
int n;
inline int read(){
int s=0,w=1;
char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}
while(ch>='0'&&ch<='9') s=s*10+ch-'0',ch=getchar();
return s*w;
}
void put(int x) {
if(x<0) putchar('-'),x=-x;
if(x>=10) put(x/10);
putchar(x%10^48);
}
int exgcd(int a, int b, int &x, int &y){
if(!b){
x=1, y=0;
return a;
}else{
int d=exgcd(b, a%b, y, x);
y-=a/b*x;
return d;
}
}
signed main(){
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
n=read();
int x=0, m1=read(), a1=read();
rep(i, 0, n-1){
int m2=read(), a2=read();
int k1, k2;
int d=exgcd(m1, m2, k1, k2);
if((a2-a1)%d){
x=-1;
break;
}
k1*=(a2-a1)/d;
k1=(k1 % (m2/d) + m2/d) % (m2/d);
x=k1*m1+a1;
int m=abs(m1/d*m2);
a1=k1*m1+a1;
m1=m;
}
if(x!=-1){
x = (a1 % m1 + m1) % m1;
}
printf("%lld",x);
return 0;
}
Originality is not easy.
Reprint please indicate the source
If it helps you Don't forget to praise and support 
边栏推荐
- 1.手动创建Oracle数据库
- Series of how MySQL works (VIII) 14 figures explain the atomicity of MySQL transactions and the principle of undo logging
- 1.13 - RISC/CISC
- C Primer Plus Chapter 15 (bit operation)
- 博弈论 AcWing 894. 拆分-Nim游戏
- 中国剩余定理 AcWing 204. 表达整数的奇怪方式
- [2021]IBRNet: Learning Multi-View Image-Based Rendering Qianqian
- Alibaba's new member "Lingyang" officially appeared, led by Peng Xinyu, Alibaba's vice president, and assembled a number of core department technical teams
- Redis publish subscribe command line implementation
- Quickly use Amazon memorydb and build your own redis memory database
猜你喜欢

2021apmcm post game Summary - edge detection
Suppose a bank's ATM machine, which allows users to deposit and withdraw money. Now there is 200 yuan in an account, and both user a and user B have the right to deposit and withdraw money from this a

5.Oracle-錶空間

4. Oracle redo log file management

求组合数 AcWing 888. 求组合数 IV
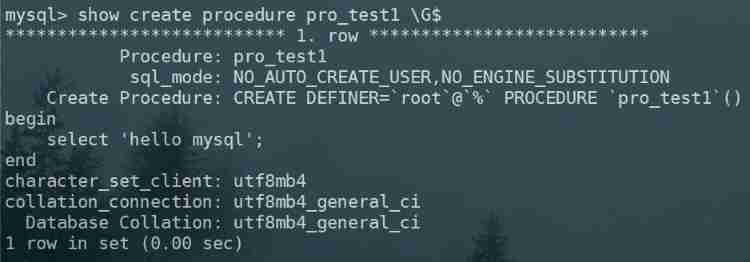
MySQL advanced part 1: stored procedures and functions

论文阅读报告

Day 2 document
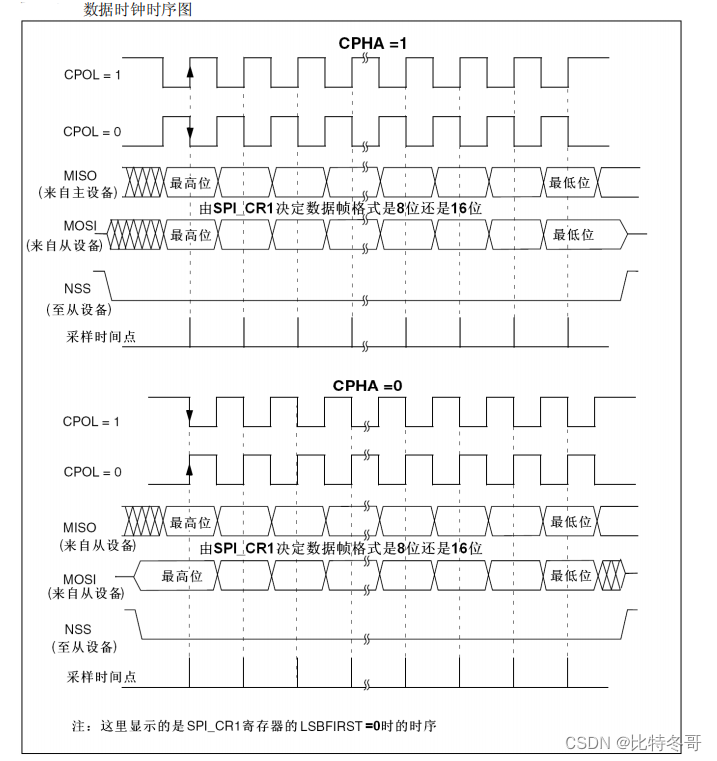
SPI details
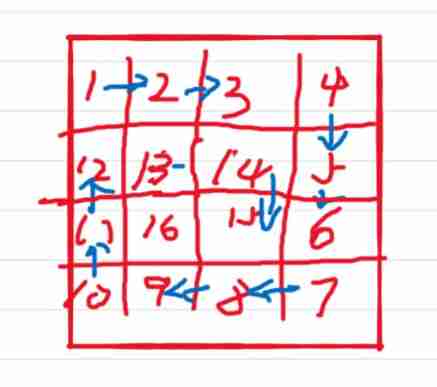
Leetcode array operation
随机推荐
[2021]IBRNet: Learning Multi-View Image-Based Rendering Qianqian
June 29, 2022 daily
2048项目实现
Navicat連接Oracle數據庫報錯ORA-28547或ORA-03135
AE tutorial - path growth animation
Leetcode-22: bracket generation
求组合数 AcWing 887. 求组合数 III
How to make water ripple effect? This wave of water ripple effect pulls full of retro feeling
Filter the numbers and pick out even numbers from several numbers
5. Oracle TABLESPACE
Leetcode stack related
LeetCode 1200. Minimum absolute difference
How to understand the definition of sequence limit?
__ builtin_ Popcount() counts the number of 1s, which are commonly used in bit operations
Leetcode-3: Longest substring without repeated characters
RecyclerView的应用
LeetCode 0107. Sequence traversal of binary tree II - another method
NotImplementedError: Cannot convert a symbolic Tensor (yolo_boxes_0/meshgrid/Size_1:0) to a numpy ar
New title of module a of "PanYun Cup" secondary vocational network security skills competition
MySQL advanced part 2: MySQL architecture