当前位置:网站首页>深度循环网络长期血压预测【翻译】
深度循环网络长期血压预测【翻译】
2022-07-06 10:43:00 【巴川笑笑生】
深度循环网络长期血压预测
摘要
现有的动脉血压(BP)估计方法直接将输入生理信号映射到输出BP值,而没有明确建模BP动态中潜在的时间依赖性。因此,这些模型的精度随着时间的推移而下降,因此需要经常校准。在这项工作中,我们通过制定BP估计作为一个序列预测问题,其中输入和目标都是时间序列来解决这个问题。我们提出了一种新的深度递归神经网络(RNN),由多层的长短时记忆(LSTM)网络组成,该网络结合了(1)双向结构,以获取更大规模的输入序列上下文信息,(2)剩余连接,使深度RNN中的梯度更有效地传播。在静态BP数据集上对所提出的深度RNN模型进行了测试,其对收缩期BP (SBP)和舒张期BP (DBP)的预测均方根误差(RMSE)分别为3.90和2.66 mmHg,超过了传统BP预测模型的精度。在多天BP数据集上,深度RNN在第1天SBP预测后第1天、第2天、第4天和第6个月的RMSE分别为3.84、5.25、5.80和5.81 mmHg,对应DBP预测RMSE分别为1.80、4.78、5.0和5.21 mmHg,优于之前所有模型,并有显著改善。实验结果表明,对BP动态中的时间依赖性建模可以显著提高BP的长期预测精度。
简介
高血压(pressure pressure, BP)作为心血管疾病(CVD)[1]的首要危险因素,已被普遍用作诊断和预防CVD的重要标准。因此,在日常生活中进行准确、持续的血压监测对心血管疾病的早期发现和干预至关重要。传统的BP测量设备,如欧姆龙产品,是基于袖口的,因此笨重,使用不舒适,只能用于快照测量。这些缺点限制了袖带式设备长期连续测量血压的使用,而袖带式设备对于夜间监测和准确诊断不同的CVD症状至关重要
心血管系统的一个关键特征是其复杂的动态自我调节,涉及多个反馈控制回路来响应BP的变化[2]。这种机制使BP动态具有时间依赖性。因此,这种依赖性对于连续的BP预测,尤其是长期的BP预测是至关重要的。
现有的无袖式连续BP估计方法可以分为两类,生理模型,即脉冲传递时间模型[3][4],回归模型,如决策树、支持向量回归等[5][6]。这些模型的精度会随着时间的推移而下降,尤其是对于多天连续的BP预测。这种局限性已经成为阻碍这些模型在实际应用中使用的瓶颈。值得注意的是,上述模型直接将当前输入映射到目标,而忽略了BP动态中重要的时间依赖性。这可能是长期不准确的根源。
与静态BP预测相比,多日BP预测通常更具挑战性。由于人体调节机制复杂,多日BP动态具有更复杂的时间依赖性和更大的变化范围。在本文中,我们将BP预测定义为一个序列学习问题,并提出了一种新的深度RNN模型,该模型被证明对BP动态中长期依赖的建模非常有效,在多日连续BP预测中达到了最先进的精度
模型
动脉血压预测的目标是利用多种时间生理信号来预测血压序列。设 X T = [ x 1 , x 2 … , x T ] X_{T} = [x_{1}, x_{2}…, x_{T}] XT=[x1,x2…,xT]为心电和PPG信号提取的输入特征, Y T = [ y 1 , y 2 … , y T ] Y_{T} = [y_{1}, y_{2}…, y_{T}] YT=[y1,y2…,yT]表示目标BP序列。条件概率 p ( Y T ∣ X T ) p(Y_{T} | X_{T}) p(YT∣XT)因式分解为
p ( Y T ∣ X T ) = ∏ t = 1 T p ( y t ∣ h t ) ( 1 ) p(Y_{T}|X_{T})=\prod_{t=1}^{T}p(y_{t}|h_{t})\quad (1) p(YT∣XT)=t=1∏Tp(yt∣ht)(1)
其中 h t h_{t} ht可以理解为BP动态系统的隐藏状态,由之前的隐藏状态 h t − 1 h_{t−1} ht−1和当前输入 x t x_{t} xt产生:
h t = f ( h t − 1 , x t ) ( 2 ) h_{t}=f(h_{t-1},x_{t})\quad (2) ht=f(ht−1,xt)(2)
图1说明了我们提出的深度RNN模型的概述。深度RNN由底层的双向LSTM和具有剩余连接的多层LSTM (Long ShortTerm Memory)组成。全网络通过时间[7]反向传播进行训练,以缩小BP预测与ground truth之间的差异。
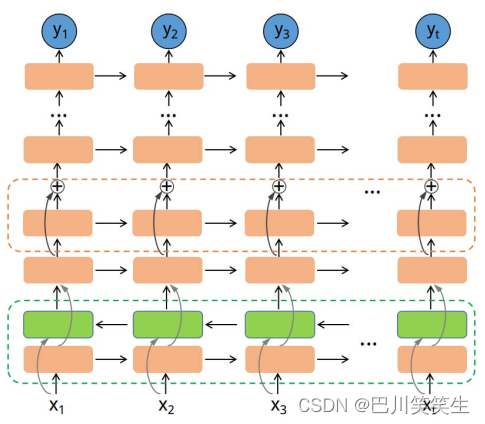
图1:DeepRNN架构。每个矩形框是一个LSTM单元。底部的绿色虚线框是一个双向LSTM层,由正向(橙色)和反向(绿色)LSTM组成。橙色的虚线框表示带有剩余连接的LSTM层。
双向LSTM结构
首先,我们引入了深度RNN模型的基本模块,即单层双向长短期记忆(LSTM)。LSTM[8]通过在标准RNN隐态转换过程中引入记忆细胞状态ct和多门控机制来解决传统RNN的消失梯度问题。LSTM中的隐藏状态 h t h_{t} ht由
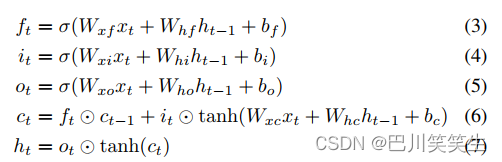
其中f、I、o分别为遗忘门、输入门、输出门,控制有多少信息将被遗忘、积累或输出。W项和b项分别表示权重矩阵和偏置向量。σ和tanh分别表示logistic s形函数和双曲正切函数的逐元应用, ⊙ \odot ⊙表示逐元乘法
传统的lstm使用ht从过去的历史中获取信息 x 1 , … x t − 1 x_{1},…x_{t-1} x1,…xt−1,现在的输入 x t x_{t} xt。为了获取更大规模的输入序列的时间上下文,还可以加入附近的未来信息 x t + 1 , … , x T x_{t+1},…, x_{T} xt+1,…,xT通知下游建模过程。双向RNN (BRNN)[9]通过两个单独的隐藏层对数据进行前向和后向处理,然后合并到同一个输出层来实现这个功能。如图1底部所示,BRNN通过下列方程计算前向隐藏态 h t f h_{t}^{f} htf、后向隐藏态 h t b h_{t}^{b} htb和最终输出 h t h_{t} ht
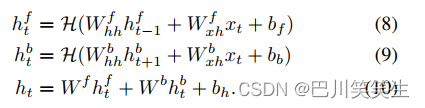
式中 H \mathcal{H} H由式3-7实现。
具有残差连接的多层架构
[10][11]的各种实验结果表明,具有深层结构的rnn可以显著优于浅层结构的rnn。只需将RNN进行多层叠加,就可以很容易地获得表达能力。然而,一个完整的深度网络随着它的深入可能会变得难以训练,可能是由于爆炸和消失的梯度问题[12]。
在相邻层之间附加一个完全复制跳连接的想法得到了启发,它在训练深度神经网络[13][14][15]方面表现出了良好的性能,我们在模型中加入了从一个LSTM层到下一个LSTM层的剩余连接,如图2所示。设 x t i x^{i}_{t} xti , h t i h^{i}_{t} hti, H i \mathcal{H}_{i} Hi分别是LSTM第 i i i层的输入,隐藏状态和LSTM函数 ( i = 1 , 2 , … , L ) (i = 1,2,…, L) (i=1,2,…,L), W i W^{i} Wi为 H i \mathcal{H}_{i} Hi对应的权值。LSTM第 i i i层的输入 x t i x_{t}^{i} xti被按元素添加到该层的隐藏状态 h t i h^{i}_{t} hti中。然后这个和 x t i + 1 x_{t}^{i+1} xti+1被送入下一层LSTM。具有剩余连接的LSTM块可以用
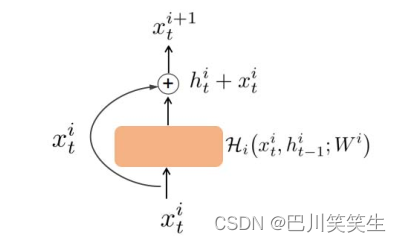
图2:带剩余连接的LSTM
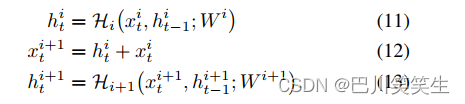
将多个这样的LSTM块相互叠加,前一个块的输出构成下一个块的输入,就可以建立深度RNN模型。一旦计算出顶层隐藏状态,可以通过下式输出 z t z_{t} zt:
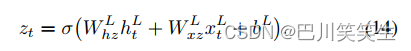
多任务训练
考虑到我们有多个监测信号,如收缩压(SBP)、舒张压(DBP)和平均BP (MBP),它们之间密切相关,我们采用多任务训练策略,训练一个模型,并行预测SBP,DBP和MBP。因此,训练目标是使总N个训练样本的均方误差(MSE)最小,如下所示
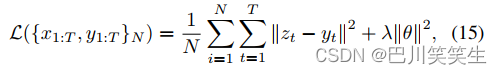
式中, y t = [ S B P , D B P , M B P ] y_{t} = [SBP, DBP, MBP] yt=[SBP,DBP,MBP]为真值, z t z_{t} zt为相应的预测。 ∣ ∣ θ ∣ ∣ 2 ||\theta||^{2} ∣∣θ∣∣2表示模型参数的 L 2 L_{2} L2正则, λ \lambda λ为对应的惩罚系数。多任务训练的一个优点是,学习同时预测不同BP值可以隐式编码SBP、DBP和MBP之间的定量约束。
深度RNN结构分析
由于它们隐藏的状态转换,rnn具有内在的深度时间。尽管所提出的深度RNN模型在时间上有一定的深度,但它沿层结构也有一定的深度。为了简化分析,这里我们主要关注沿层深的梯度流动。通过递归更新方程(12),我们将有
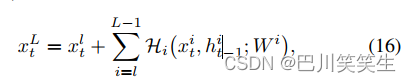
对于任何较深的层 L L L和较浅的层 l l l。方程(16)可以得到很好的反向传播特性。将损失函数记为 L \mathcal{L} L,根据反向传播的链式法则
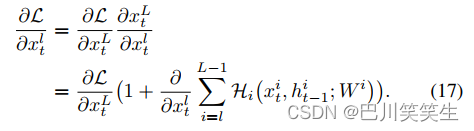
方程(17)表示梯度 ∂ L ∂ x t l \frac{\partial \mathcal{L}}{\partial x_{t}^{l}} ∂xtl∂L可以分解为两个相加项:一项 ∂ L ∂ x t L \frac{\partial \mathcal{L}}{\partial x_{t}^{L}} ∂xtL∂L直接传播信息,不通过任何权重层,另一项 ∂ L ∂ x t l ( ∂ ∂ x ∑ i = l L − 1 H i ) \frac{\partial \mathcal{L}}{\partial x_{t}^{l}}(\frac{\partial }{\partial x}\sum_{i=l}^{L-1}\mathcal{H}_{i}) ∂xtl∂L(∂x∂∑i=lL−1Hi)。的第一项 ∂ L ∂ x t L \frac{\partial \mathcal{L}}{\partial x_{t}^{L}} ∂xtL∂L确保该监督信息可以直接反向传播到任何较浅的层 x t l x_{t}^{l} xtl。一般来讲 ∂ ∂ x ∑ i = l L − 1 H i \frac{\partial }{\partial x}\sum_{i=l}^{L-1}\mathcal{H}_{i} ∂x∂∑i=lL−1Hi对于小批量的所有样本,不能总是−1,所以梯度 ∂ L ∂ x t l \frac{\partial \mathcal{L}}{\partial x_{t}^{l}} ∂xtl∂L不太可能被抵消。这意味着即使中间权重是任意小的,一层的梯度也不会消失。这种良好的反向传播特性使我们能够训练出具有更强表达能力的深度RNN模型,而无需担心梯度消失问题。
实验
我们在静态和多日连续BP数据集上评估了所提出的模型。均方根误差(RMSE)作为评价指标,其定义为
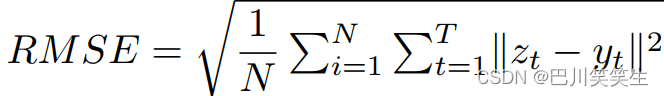
在这两个数据集上,我们将我们的模型与以下参考模型进行比较
- 脉冲传输时间(PTT)模型:我们选取两个被引用最多的模型基于pt的模型——Chen的方法[3]1和Poon的方法[4]。
- 典型的回归模型:支持向量回归(SVR)、决策树(DT)和贝叶斯线性回归(BLR)。
- 卡尔曼滤波器
数据集
静态连续BP数据集。数据集包括心电图、PPG和BP,来自84例健康人群,其中男性51例,女性33例。每次实验均采用Biopac系统采集心电图和PPG信号,Finapres系统同时测量连续基准BP值。静息状态下,以1000 Hz采样频率记录每位受试者的BP、ECG和PPG数据,持续10分钟。
多天连续BP数据集。类似的数据集取自12名健康受试者,包括11名男性和1名女性。记录每位受试者静息状态下的BP、ECG和PPG数据,多日期,即第1天、第2天、第4天和第1天后6个月,共8分钟。
数据表示
由于本文的主要目标是证明BP动态中建模时间相关性对准确BP预测的重要性,我们简单地选择了ECG和PPG信号的7个代表性手工特征(如图3所示)如下:
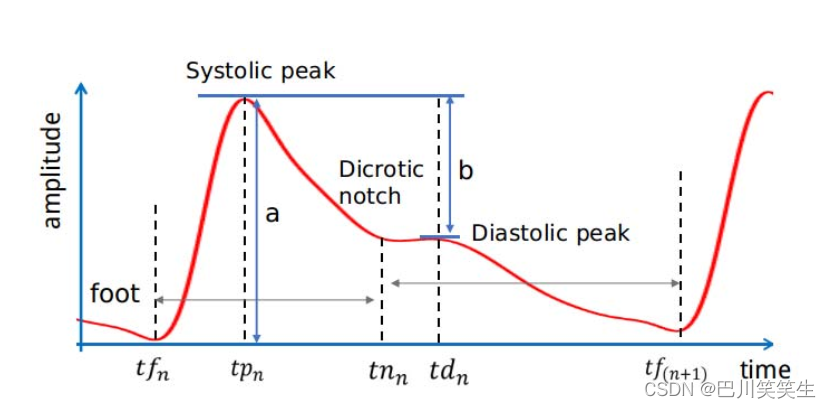
图3:PPG特征示意图
- P T T S PTT_{S} PTTS:从心电图R峰值到同一心脏周期PPG最大斜率的时间间隔。
- 心率HR
- 反射率 R I = b / a RI=b/a RI=b/a
- 收缩时间间隔 S T = t n n − t f n ST=tn_{n}-tf_{n} ST=tnn−tfn
- 上升时间$upTime = tp_{n} - tf_{n} $
- 心缩容积 S V = ∫ t n n t f n P P G ( t ) d t SV=\int_{tn_{n}}^{tf_{n}}PPG(t)dt SV=∫tnntfnPPG(t)dt
- 心舒容积 D V = ∫ t n n t f n + 1 P P G ( t ) d t DV=\int_{tn_{n}}^{tf_{n}+1}PPG(t)dt DV=∫tnntfn+1PPG(t)dt
现在输入 X T X_{T} XT变成了一个 7 × T 7\times T 7×T的矩阵, X T X_{T} XT的每一行都被归一化为零均值和单位方差。通过添加更多信息特性作为模型输入,可以期望进一步提高模型性能。
结果
静态连续BP数据集的验证。如表1所示,PTT模型的结果略好于BLR和SVR模型,但性能较DT、卡尔曼滤波、双向LSTM和深度RNN (DeepRNN)模型差。4层深度RNN (DeepRNN-4L)模型对SBP和DBP的预测精度最高,RMSE分别为3.73和2.43。Bland-Altman图(图4)表明,DeepRNN- 4L预测与真实值吻合良好,95%的差异位于一致区域内。图6定性地展示了静态连续BP数据集对一个代表性主体的DeepRNN-4L预测结果。
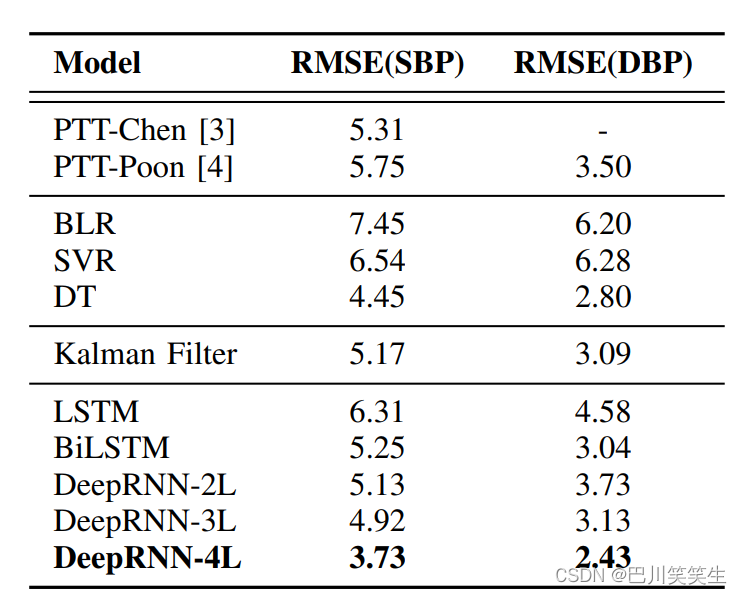
表一:详细分析了我们的Deep RNN模型,并与不同的参考模型进行了比较。DeepRNN-xL表示x层RNN模型。在静态连续BP数据集上对所有模型进行了验证。(单位:毫米汞柱)
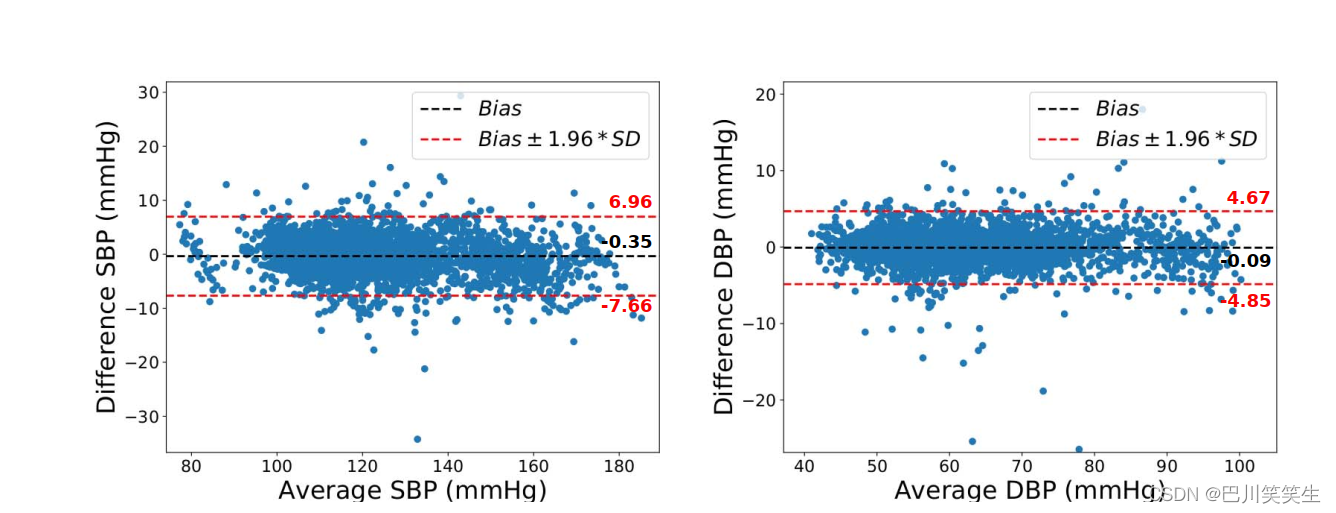
图4:在静态连续BP数据集上,DeepRNN-4L模型对总体SBP和DBP预测的Bland-Altman图。
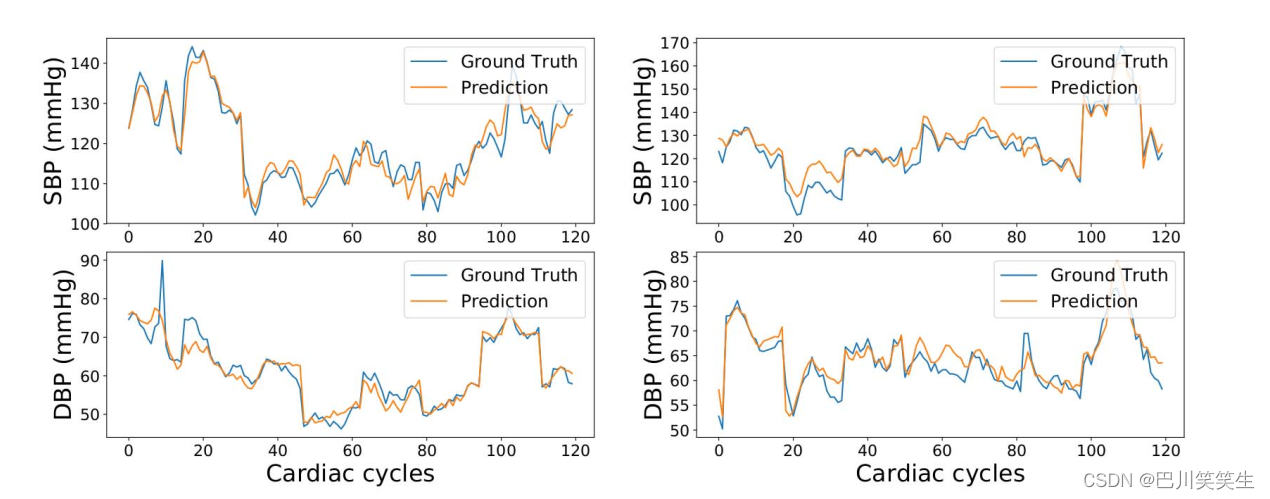
图6:静态连续BP数据集中两个代表性对象的ground truth和DeepRNN预测结果对比。每一栏表示一个被试的收缩压和舒张压预测。
通过在模型中加入双向结构,即使用双向LSTM (BiLSTM),与普通LSTM相比,预测精度显著提高,SBP RMSE降低17%,DBP RMSE降低34%。此外,还发现随着深度的增加,深度神经网络的预测精度的提高也在增强。例如,用DeepRNN-4L替代DeepRNN-2L,对SBP和DBP的预测分别提高了27%和35%。当我们叠加到一个5层的DeepRNN时,模型倾向于过拟合,不能再观察到明显的深度优势
多天连续BP数据集的验证。图5比较了深度RNN与参考模型的预测性能。可以清楚地看到,与PTT和回归模型相比,DeepRNN模型产生了更好的性能,这可能是由于在DeepRNN模型中的时间依赖性建模。卡尔曼滤波可以对时序依赖性进行建模,但其性能不如深度prnn模型。由于卡尔曼滤波的线性假设,很可能状态转移和测量函数都是线性的。这种假设可能会限制其对BP动态中复杂的时间依赖性建模的能力。深度prnn - 4l模型在第1天SBP预测后第1天、第2天、第4天和第6个月的精度最高,RMSE分别为3.84、5.25、5.80和5.81 mmHg, DBP预测的RMSE分别为1.80、4.78、5.0和5.21 mmHg。如图5所示,所有的PTT模型、回归模型和卡尔曼滤波器在第二天都表现出明显的精度衰减。虽然在第一天之后,DeepRNN模型的预测精度也有所下降,但其RMSE值始终是所有模型中最低的。图7定性地展示了DeepRNN跟踪BP长期变化的能力。
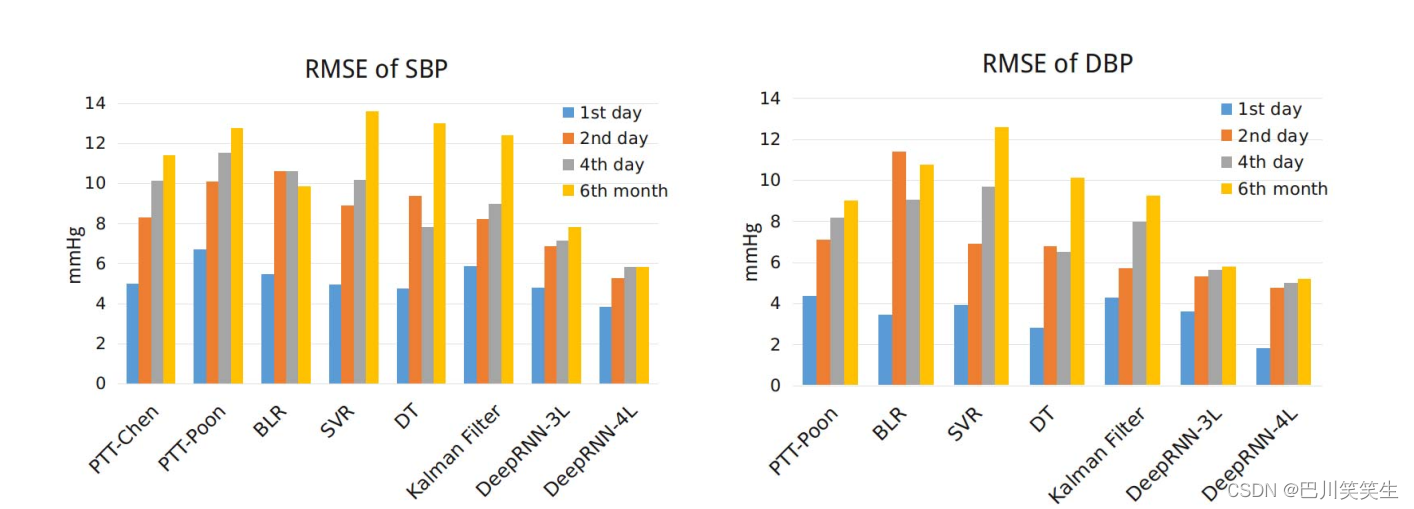
图5:不同模型在多日连续BP数据集上的总体RMSE比较
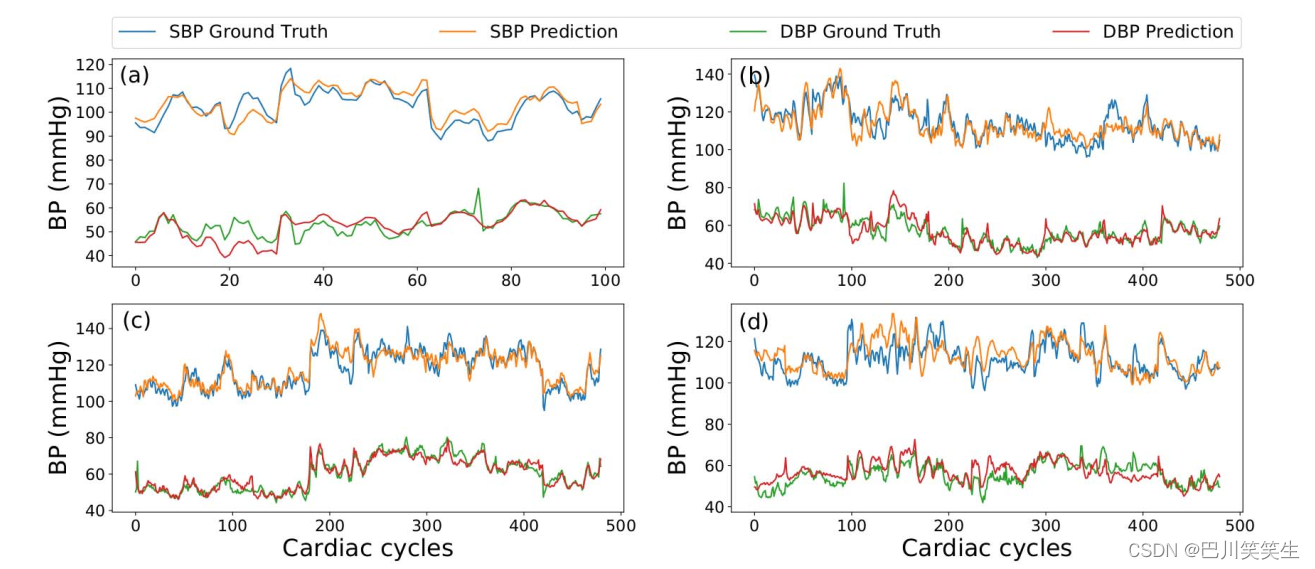
图7:多日连续BP数据集中一个代表性对象的ground truth和DeepRNN预测结果对比。图(a)、(b)、和(d)分别为第1天、第2天、第4天和第6个月的结果。
残差连接的重要性。为了研究剩余连接的重要性,我们对静态连续BP数据集进行了消融研究。如表2所示,加入剩余连接的DeepRNN模型的工作效果要比对应的模型好得多。在训练过程中,我们发现残差连接显著改善了向后传递中的梯度流,使深度神经网络更容易优化。因此,表现力更强的深层结构可以获得更好的性能。这种计算效益的详细原因已在第三节中解释。

表二:有残留连接与无残留连接的DeepRNN-4L模型性能比较。结果是在静态连续的BP数据集上得到的。(单位:毫米汞柱)
多任务训练的重要性。由表三可以看出,多任务训练策略相比单个模型的单独训练能够提高预测性能。这可以解释为,每个任务所涉及的不同训练目标都是强相关的,因此共享了许多捕获底层因素的数据表示,这些数据表示可以通过相同的模型结构学习。因此,通过学习共享表示,可以极大地提高模型泛化能力。
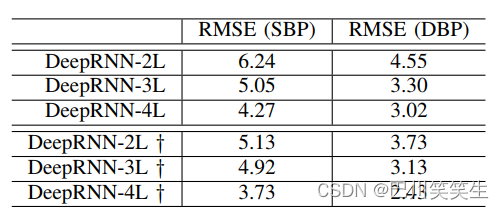
表三:不同设置下的DeepRNN调查。使用多任务目标训练的模型标记为’†'。结果是在静态连续的BP数据集上得到的。(单位:毫米汞柱)
结论
模型结构学习。因此,通过学习共享表示,可以极大地提高模型泛化能力。
[外链图片转存中…(img-Lcy4Ylj5-1656835802157)]
表三:不同设置下的DeepRNN调查。使用多任务目标训练的模型标记为’†'。结果是在静态连续的BP数据集上得到的。(单位:毫米汞柱)
结论
在这项工作中,我们证明了BP动态的时间依赖性建模可以显著提高BP的长期预测精度,这是无袖BP估计中最具挑战性的问题之一。为了解决这一问题,我们提出了一种新的深度RNN,它结合了双向LSTM和剩余连接。实验结果表明,深度RNN模型在静态和多天连续BP数据集上均达到了最先进的精度。
边栏推荐
- [the 300th weekly match of leetcode]
- 随着MapReduce job实现去加重,多种输出文件夹
- STM32+MFRC522完成IC卡号读取、密码修改、数据读写
- Stm32+hc05 serial port Bluetooth design simple Bluetooth speaker
- [Sun Yat sen University] information sharing of postgraduate entrance examination and re examination
- Recommend easy-to-use backstage management scaffolding, everyone open source
- Huawei 0 foundation - image sorting
- Recursive way
- 测试行业的小伙伴,有问题可以找我哈。菜鸟一枚~
- UDP protocol: simple because of good nature, it is inevitable to encounter "city can play"
猜你喜欢
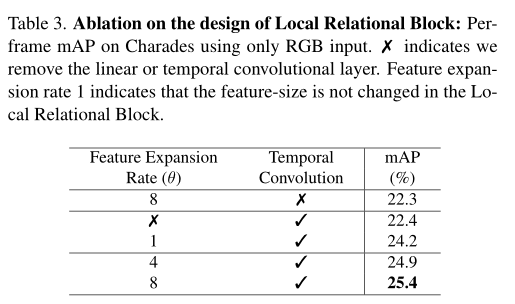
Ms-tct: INRIA & SBU proposed a multi-scale time transformer for motion detection. The effect is SOTA! Open source! (CVPR2022)...

Penetration test information collection - CDN bypass
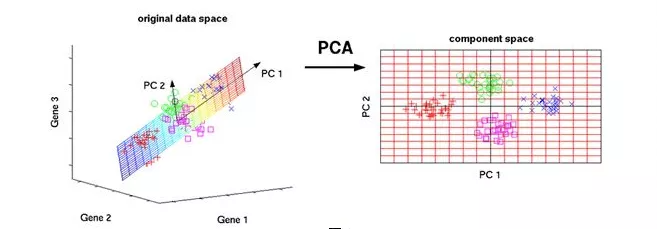
30 minutes to understand PCA principal component analysis
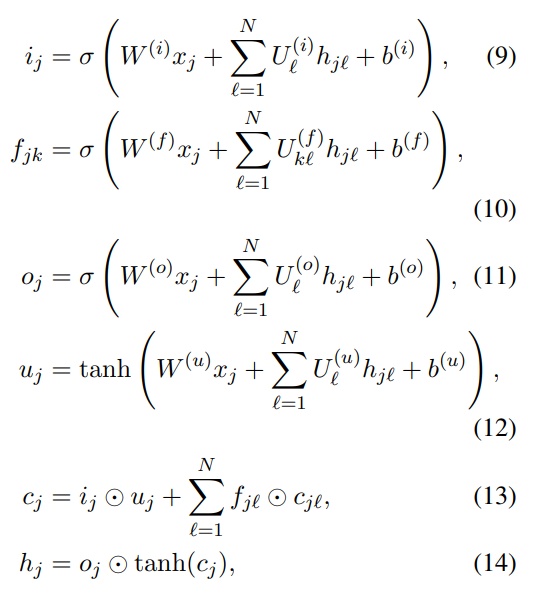
Some understandings of tree LSTM and DGL code implementation
![[Matlab] Simulink 同一模块的输入输出的变量不能同名](/img/99/adfe50075010916439cd053b8f04c7.png)
[Matlab] Simulink 同一模块的输入输出的变量不能同名

Declval of template in generic programming

重磅硬核 | 一文聊透对象在 JVM 中的内存布局,以及内存对齐和压缩指针的原理及应用
Easy to use PDF to SVG program
Penetration test information collection - WAF identification
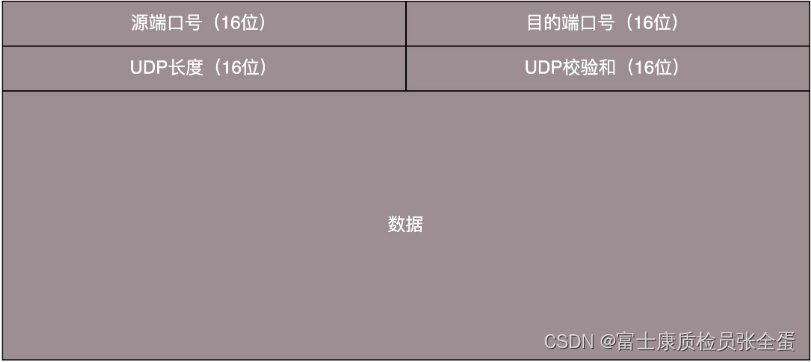
UDP协议:因性善而简单,难免碰到“城会玩”
随机推荐
C语言高校实验室预约登记系统
监控界的最强王者,没有之一!
2022-2024年CIFAR Azrieli全球学者名单公布,18位青年学者加入6个研究项目
AFNetworking框架_上传文件或图像server
推荐好用的后台管理脚手架,人人开源
当保存参数使用结构体时必备的开发技巧方式
Distill knowledge from the interaction model! China University of science and Technology & meituan proposed virt, which combines the efficiency of the two tower model and the performance of the intera
用友OA漏洞学习——NCFindWeb 目录遍历漏洞
287. 寻找重复数
Echart simple component packaging
SAP Fiori 应用索引大全工具和 SAP Fiori Tools 的使用介绍
Alibaba cloud international ECS cannot log in to the pagoda panel console
A method of sequentially loading Unity Resources
Penetration test information collection - basic enterprise information
复现Thinkphp 2.x 任意代码执行漏洞
TOP命令详解
2022 Summer Project Training (II)
Self-supervised Heterogeneous Graph Neural Network with Co-contrastive Learning 论文阅读
Unity资源顺序加载的一个方法
测试行业的小伙伴,有问题可以找我哈。菜鸟一枚~