当前位置:网站首页>LeetCode41——First Missing Positive——hashing in place & swap
LeetCode41——First Missing Positive——hashing in place & swap
2022-07-06 08:56:00 【Zheyuan Zou】
这道题让我们找出一个数组中的缺失的第一个元素,也就是最小的一个正数,题面如下: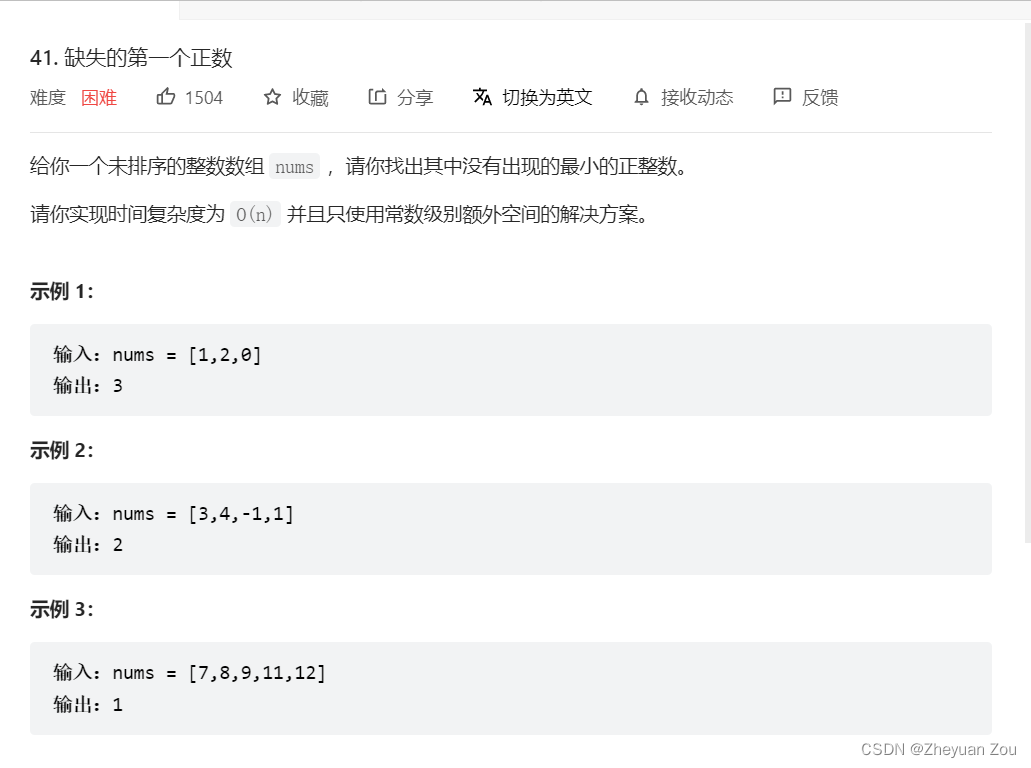
其实如果只实现这个功能的话并不难,难点在于题目中对算法的时间和空间复杂度同时做出了约束,即时间复杂度是 O ( n ) O(n) O(n),与此同时空间复杂度是 O ( 1 ) O(1) O(1)。
在完成这道题之前,有一个点非常重要的观察就是:
对于长度为N的数组nums,其最小缺失的正数只会位于区间 [ 1 , N + 1 ] [1, N + 1] [1,N+1]内,也就是说,长度为N的数组最多只会占用 [ 1 , N ] [1,N] [1,N]这N个正整数,从而使缺失的第一个正整数是N+1。其他特殊情况包括数组中存在大于N的正整数,或是非正整数(<=0的数),都会使得缺失的最小正整数落在 [ 1 , N ] [1,N] [1,N]这个范围内,这个结论是完成这个问题的前提。
时间复杂度和空间复杂度都是 O ( n ) O(n) O(n)的算法可以是申请一个长度为n的数组Flag表示 [ 1 , N ] [1,N] [1,N],为了方便这里我多取一个元素,然后逐一标记在nums中出现的元素,随后看首个没有出现的正数是多少就可以了。代码如下:
int firstMissingPositive(vector<int>& nums) {
/*O(n)-O(n) algorithm*/
/*apply for a flag array to record existing element*/
bool* Flag = new bool [nums.size() + 1];
for(int i = 0 ; i <= nums.size() ; ++i)
Flag[i] = false;
/*set flag[nums[i]] as true when nums[i]∈[1, N]*/
size_t Size = nums.size();
int Result = Size + 1;
for(int i = 0 ; i < nums.size() ; ++i)
if(nums[i] > 0 && nums[i] <= Size)
Flag[nums[i]] = true;
/*search for the first missing positive number*/
for(int i = 1 ; i <= nums.size() ; ++i)
if(!Flag[i])
{
Result = i;
break;
}
delete [] Flag;
return Result;
}
这种朴素的方式增加了空间复杂度,减少了时间复杂度,只需要遍历2次数组就可以。但是还是没有达到题目要求的同时兼顾时间复杂度和空间复杂度的要求,这里有两种方法达成这一目标(从官方题解学的,哭:(:
一、就地哈希(hashing in place)
这种方式主要就是在原有的nums数组中完成 [ 1 , N ] [1,N] [1,N]的标记,这个算法分以下几步:
- 遍历nums第一次,将其中小于等于0的元素全部修改为N+1,N是数组长度。这是因为后续要用数组中的元素减去1作为下标去标记nums中的元素。负数和0减去1之后索引值会变成负值。修改成N+1之后就会消除掉这个问题,而且N+1-1 = N,它不会标记到nums中的任何元素(nums最大可用索引是N-1)。
- 遍历nums第二次,将nums数组中介于范围 [ 1 , N ] [1,N] [1,N]中的元素值减去1作为下标,将对应下标的元素置为负数以表示此元素存在。
- 遍历nums第三次,看看第一个正整数出现在nums中的哪一位,假设数组中第i位是正数,那么说明此索引对应的正数i+1从未出现过。假设都是负数,那么说明第一个未出现的正数是N+1。
以下是实现的源代码:
int firstMissingPositive(vector<int>& nums) {
int Size = nums.size();
/*Iteration 1*/
for(int i = 0 ; i < Size ; ++i)
if(nums[i] <= 0)
nums[i] = Size + 1;
/*Iteration 2*/
for(int i = 0 ; i < Size ; ++i)
{
int num = abs(nums[i]); // num must be larger than 0
if(num <= Size) // make sure the num is less than N
nums[num - 1] = -abs(nums[num - 1]); // make sure the value is negative
}
/*Iteration 3*/
for(int i = 0 ; i < Size ; ++i)
if(nums[i] > 0)
return i + 1;
return Size + 1;
}
二、就地交换(swap)
这个算法来得比就地哈希还简单,它的核心思想是将每一个元素放到它“应该在”的位置。具体来说,一个值为 x ∈ [ 1 , N ] x \in [1,N] x∈[1,N]的元素,它应该在索引为x-1的位置,我们这时候只需要交换它和它应该在的位置上的元素即可。
但是要注意这个交换并不是一蹴而就的,新换过来的元素同样需要把它安排到它应该在的位置,所以这是一个循环的逻辑。最后还有一种特殊情况需要讨论,那就是如果交换的这个两个元素一样,就会陷入死循环(两个元素不停的换来换去),所以循环的条件中要加上对这种情况的讨论和避免。
最后检查一下nums数组,第一个出现在它不应该出现在的位置上的元素就是缺失的最小正数。
整体的代码如下:
int firstMissingPositive(vector<int>& nums) {
int Size = nums.size();
for(int i = 0 ; i < Size ; ++i)
{
/*2 conditions:*/
/*1.nums[i] ∈ [1,N]*/
/*2.avoid infinite loop*/
while(nums[i] > 0 && nums[i] <= Size && nums[i] != nums[nums[i] - 1])
swap(nums[i], nums[nums[i] - 1]);
}
for(int i = 0 ; i < Size ; ++i)
if(nums[i] != i + 1)
return i + 1;
return Size + 1;
}
边栏推荐
猜你喜欢
Target detection - pytorch uses mobilenet series (V1, V2, V3) to build yolov4 target detection platform
View computer devices in LAN
JVM quick start
TP-LINK 企业路由器 PPTP 配置
多元聚类分析
MYSQL卸载方法与安装方法
LeetCode:124. Maximum path sum in binary tree
【ROS】usb_ Cam camera calibration
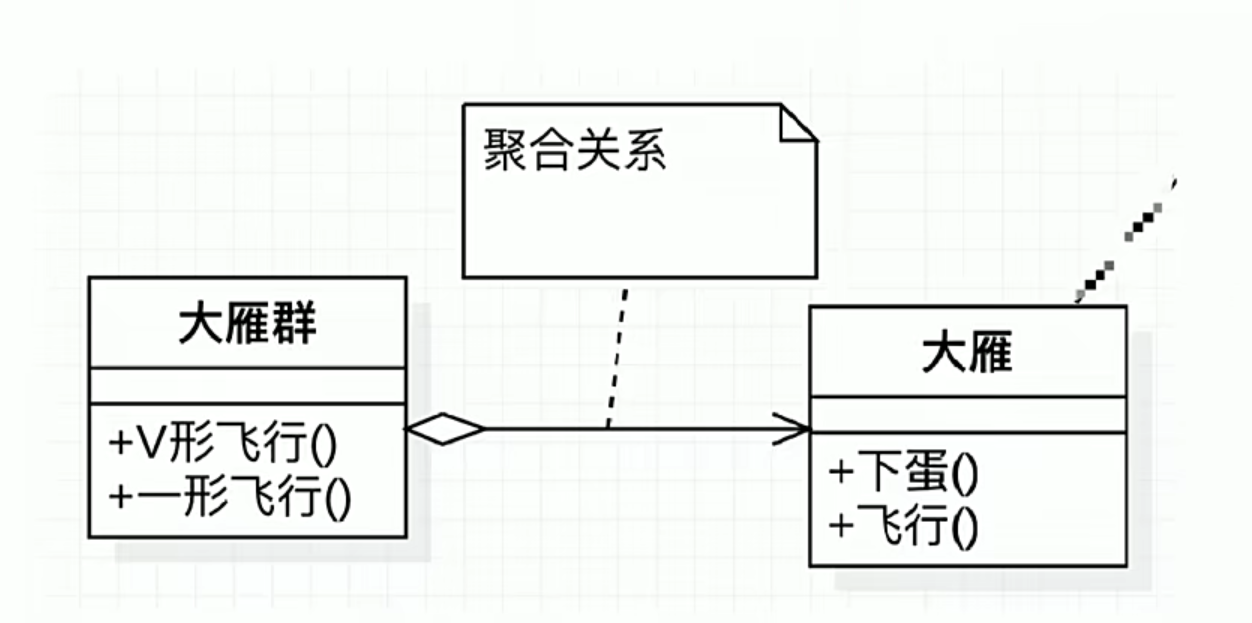
UML图记忆技巧
After PCD is converted to ply, it cannot be opened in meshlab, prompting error details: ignored EOF
随机推荐
TCP/IP协议
What is an R-value reference and what is the difference between it and an l-value?
Navicat premium create MySQL create stored procedure
LeetCode:498. Diagonal traversal
swagger设置字段required必填
Indentation of tabs and spaces when writing programs for sublime text
数学建模2004B题(输电问题)
vb. Net changes with the window, scales the size of the control and maintains its relative position
CSP first week of question brushing
[OC]-<UI入门>--常用控件-UIButton
UnsupportedOperationException异常
LeetCode:498. 对角线遍历
多元聚类分析
Detailed explanation of heap sorting
Tcp/ip protocol
ant-design的走马灯(Carousel)组件在TS(typescript)环境中调用prev以及next方法
Leetcode: Sword finger offer 42 Maximum sum of continuous subarrays
Deep anatomy of C language -- C language keywords
R language ggplot2 visualization: place the title of the visualization image in the upper left corner of the image (customize Title position in top left of ggplot2 graph)
Niuke winter vacation training 6 maze 2