当前位置:网站首页>OpenGL - Coordinate Systems
OpenGL - Coordinate Systems
2022-07-05 09:12:00 【农场主er】
从顶点坐标到我们最终看到的效果,中间要经历多个坐标系的转换: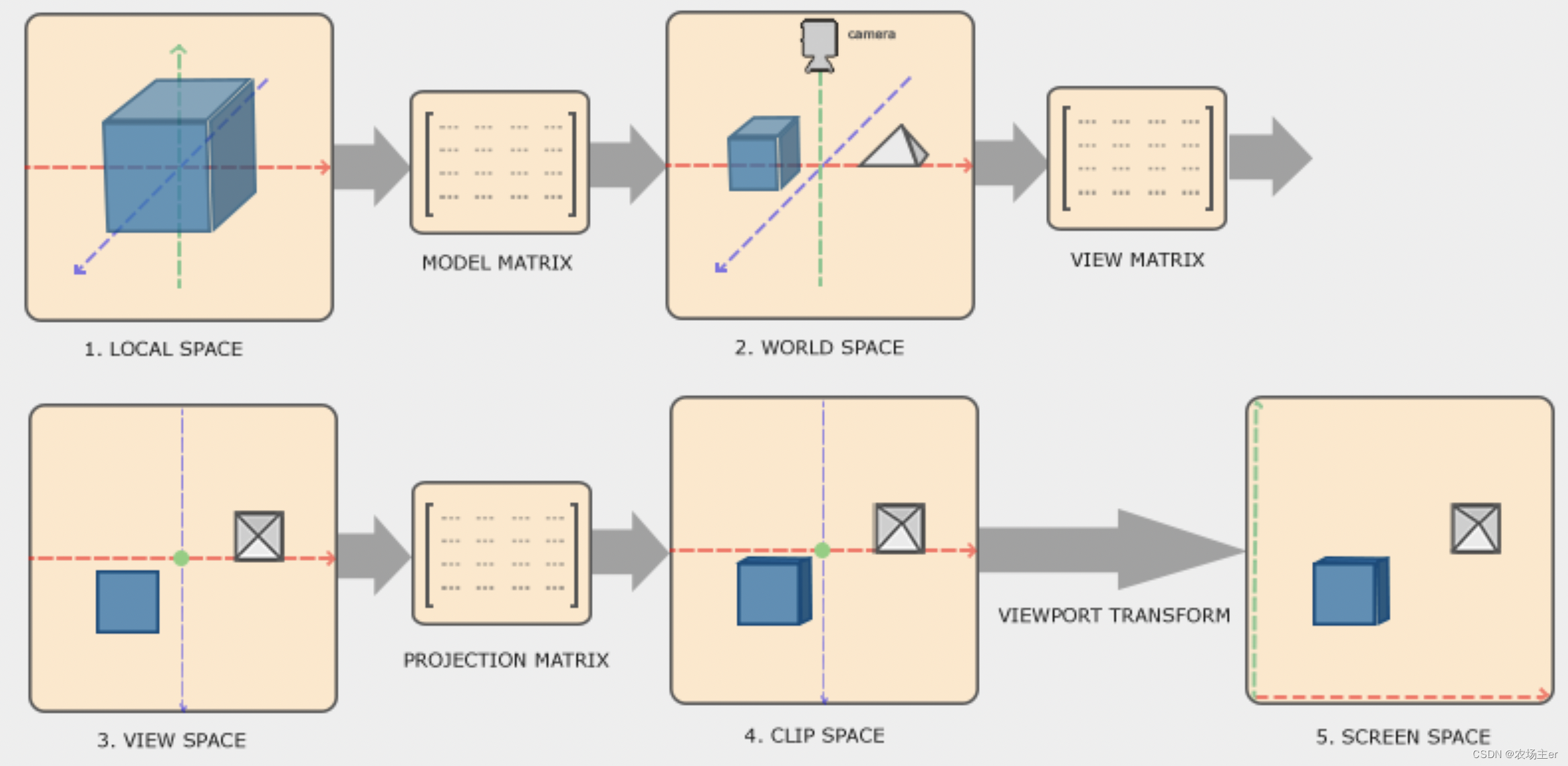
对于我们来讲,只需要关注三个矩阵即可:Vclip=Mprojection⋅Mview⋅Mmodel⋅Vlocal
Mmodel:将局部坐标转为世界坐标的矩阵,注意此时的平移是以物体本身的坐标系为基准的Mview:将世界坐标以摄像机的视角进行转换,比如向右平移,实际上视图会向左平移Mprojection:对观察坐标进行投影
Camera/View space
通过view matrix,将世界坐标系相对摄像机的位置和方向进行转换,就可以得到view space。摄像机在世界坐标系的位置定义如下: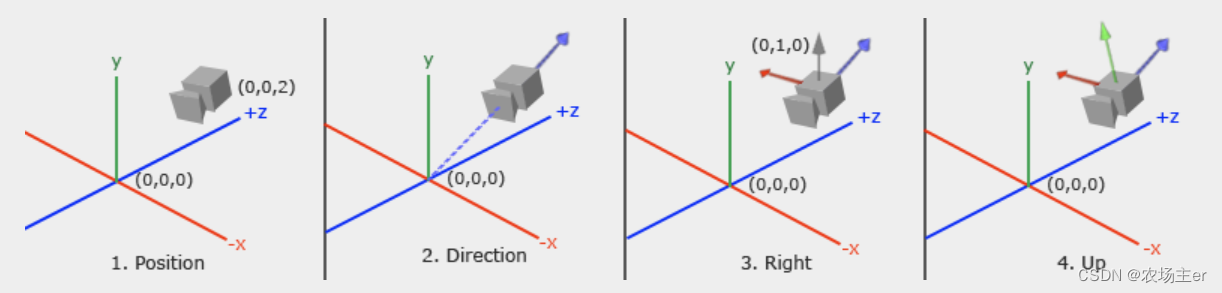
glm::vec3 cameraPos = glm::vec3(0.0f, 0.0f, 3.0f);
glm::vec3 cameraTarget = glm::vec3(0.0f, 0.0f, 0.0f);
glm::vec3 cameraDirection = glm::normalize(cameraPos - cameraTarget);
glm::vec3 up = glm::vec3(0.0f, 1.0f, 0.0f);
glm::vec3 cameraRight = glm::normalize(glm::cross(up, cameraDirection));
glm::vec3 cameraUp = glm::cross(cameraDirection, cameraRight);
有了位置信息之后,可以计算出LookAt matrix: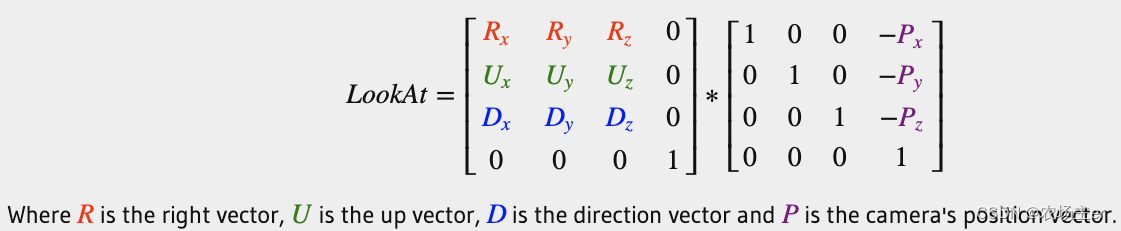
利用glm可以更便捷的构造出该矩阵:
glm::mat4 view;
// Position Target Up
view = glm::lookAt(glm::vec3(0.0f, 0.0f, 3.0f),
glm::vec3(0.0f, 0.0f, 0.0f),
glm::vec3(0.0f, 1.0f, 0.0f));
Walk around
Look around
Euler angles
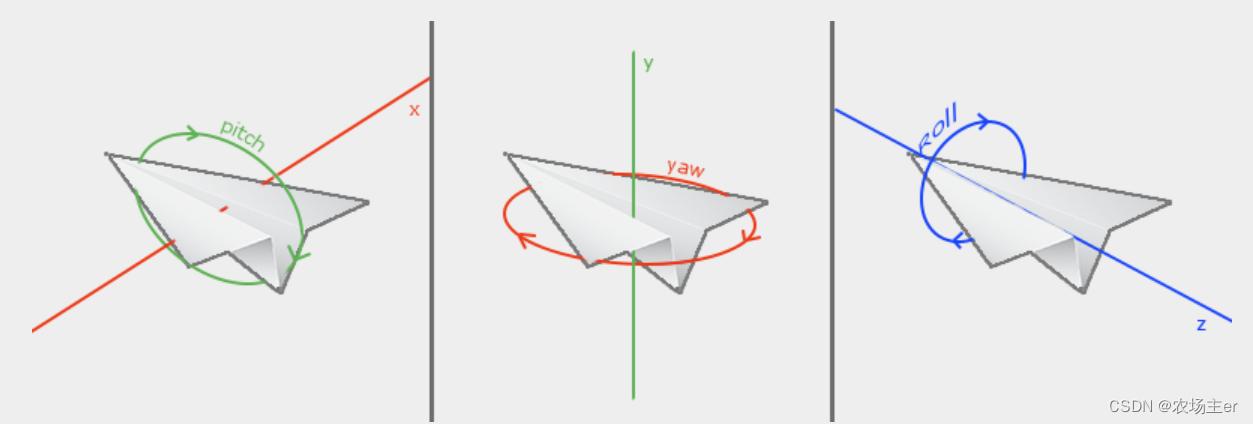
俯仰角(pitch)是描述我们如何往上或往下看的角,可以在第一张图中看到。第二张图展示了偏航角(yaw),表示我们往左和往右看的程度。滚转角(roll)代表我们如何翻滚摄像机,通常在太空飞船的摄像机中使用。
鼠标左右移动改变了yaw,上下移动改变了pitch,变换的坐标可以计算为:
glm::vec3 direction;
// yaw 在xz平面, pitch 在yz平面
direction.x = cos(glm::radians(yaw)) * cos(glm::radians(pitch));
direction.y = sin(glm::radians(pitch));
direction.z = sin(glm::radians(yaw)) * cos(glm::radians(pitch));
Zoom
Camera Class
边栏推荐
- Use arm neon operation to improve memory copy speed
- [daiy4] jz32 print binary tree from top to bottom
- Chris LATTNER, the father of llvm: why should we rebuild AI infrastructure software
- Huber Loss
- C#绘制带控制点的Bezier曲线,用于点阵图像及矢量图形
- 我的一生.
- Jenkins Pipeline 方法(函数)定义及调用
- 容易混淆的基本概念 成员变量 局部变量 全局变量
- Ros- learn basic knowledge of 0 ROS - nodes, running ROS nodes, topics, services, etc
- [code practice] [stereo matching series] Classic ad census: (5) scan line optimization
猜你喜欢
容易混淆的基本概念 成员变量 局部变量 全局变量
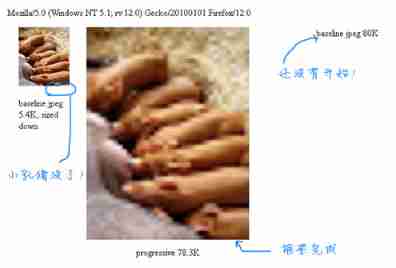
Progressive JPEG pictures and related
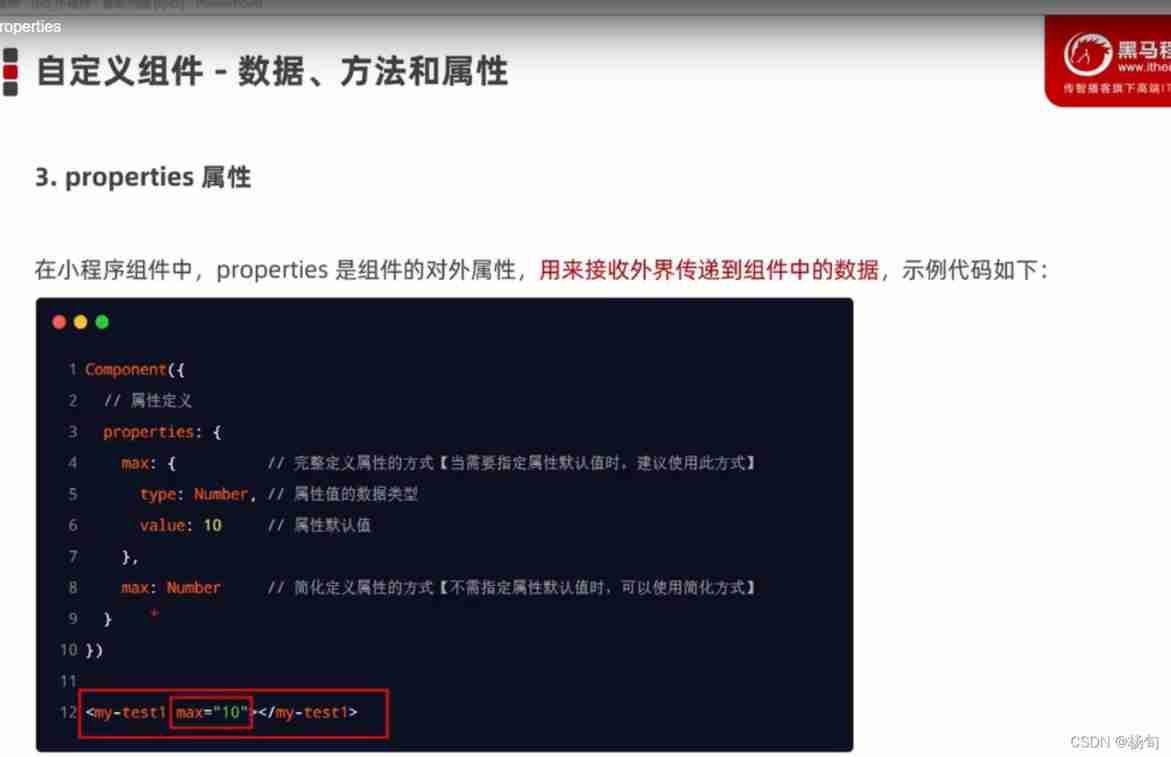
Applet data attribute method
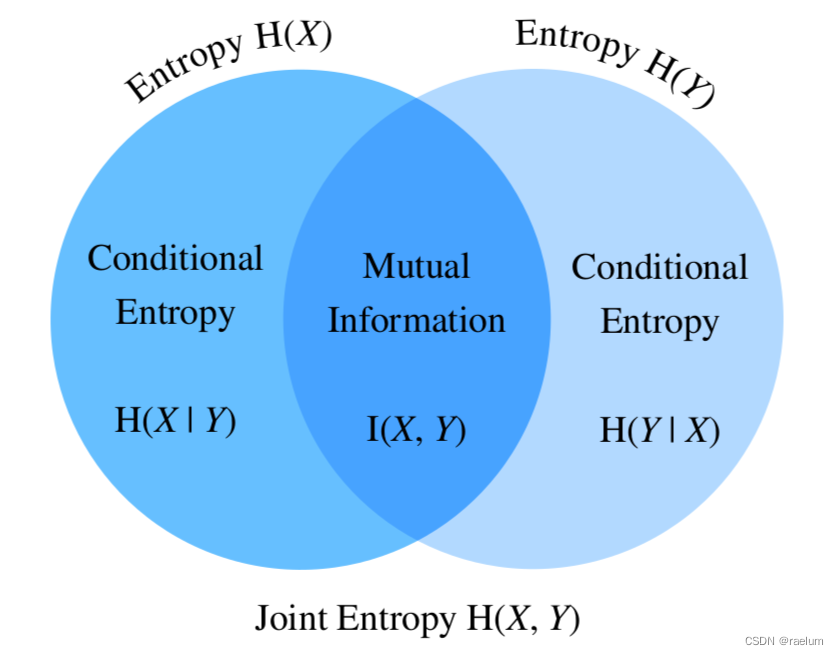
Information and entropy, all you want to know is here
Applet (global data sharing)
![3D reconstruction open source code summary [keep updated]](/img/ec/984aede7ef9e758abd52fb5ff4e144.jpg)
3D reconstruction open source code summary [keep updated]

信息與熵,你想知道的都在這裏了

Composition of applet code
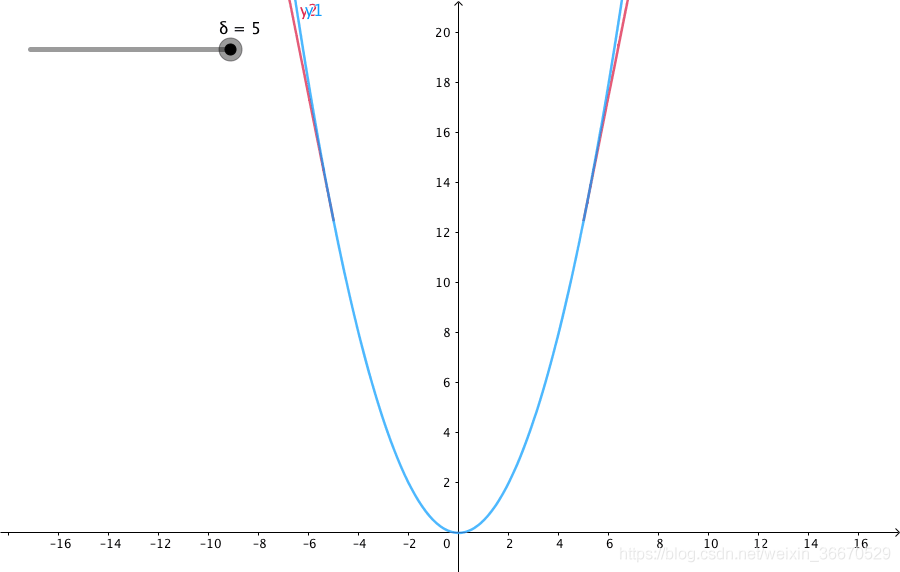
Huber Loss
Use and programming method of ros-8 parameters
随机推荐
【PyTorch Bug】RuntimeError: Boolean value of Tensor with more than one value is ambiguous
信息与熵,你想知道的都在这里了
信息與熵,你想知道的都在這裏了
ROS learning 1- create workspaces and function packs
scipy. misc. imread()
Add discount recharge and discount shadow ticket plug-ins to the resource realization applet
[code practice] [stereo matching series] Classic ad census: (6) multi step parallax optimization
Use arm neon operation to improve memory copy speed
Nodemon installation and use
2020 "Lenovo Cup" National College programming online Invitational Competition and the third Shanghai University of technology programming competition
22-07-04 西安 尚好房-项目经验总结(01)
[beauty of algebra] singular value decomposition (SVD) and its application to linear least squares solution ax=b
12. Dynamic link library, DLL
C # compare the differences between the two images
Talking about label smoothing technology
Introduction Guide to stereo vision (2): key matrix (essential matrix, basic matrix, homography matrix)
ORACLE进阶(三)数据字典详解
Wxss template syntax
Introduction Guide to stereo vision (6): level constraints and polar correction of fusiello method
微信H5公众号获取openid爬坑记