当前位置:网站首页>[statistical learning methods] learning notes - Chapter 4: naive Bayesian method
[statistical learning methods] learning notes - Chapter 4: naive Bayesian method
2022-07-07 12:34:00 【Sickle leek】
Statistical learning methods learning notes : Naive bayes method
Naive bayes method (Naive Bayes) Is based on Bayes theorem And Independent hypothesis of characteristic conditions The classification of . For a given set of training data , First, we assume that the learning input is independent based on the feature conditions / Joint probability distribution of output ; And then based on this model , For the given input x x x, Using Bayes theorem to find the maximum posterior probability y y y. 1. Learning and classification of naive Bayes
1.1 The basic method
Set input space X ⊆ R n \mathcal{X} \subseteq R^n X⊆Rn by n A set of dimensional vectors , The output space is a collection of class tags Y = { c 1 , c 2 , . . . , c K } \mathcal{Y}=\{c_1,c_2,...,c_K\} Y={ c1,c2,...,cK}. The input is the eigenvector x ∈ X x\in \mathcal{X} x∈X, The output is a class tag (class label) y ∈ Y y \in \mathcal{Y} y∈Y. X X X It's defined in the input space X \mathcal{X} X A random vector on a vector , Y Y Y Is defined in the output space Y \mathcal{Y} Y The random variable on , P ( X , Y ) P(X,Y) P(X,Y) yes X X X and Y Y Y The joint probability distribution of . Training data set T = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x N , y N ) } T=\{(x_1,y_1),(x_2,y_2),...,(x_N,y_N)\} T={ (x1,y1),(x2,y2),...,(xN,yN)}, from P ( X , Y ) P(X,Y) P(X,Y) Independent identically distributed .
Naive Bayesian method learns joint probability distribution through training data set P ( X , Y ) P(X,Y) P(X,Y). In particular , Learn the following A priori probability distribution as well as Conditional probability distribution .
- A priori probability distribution P ( Y = c k ) , k = 1 , 2 , . . . , K P(Y=c_k),k=1,2,...,K P(Y=ck),k=1,2,...,K
- Conditional probability distribution : P ( X = x ∣ Y = c k ) = P ( X ( 1 ) = x ( 1 ) , . . . , X ( n ) = x ( n ) ∣ Y = c k ) , k = 1 , 2... , K P(X=x|Y=c_k)=P(X^{(1)}=x^{(1)},...,X^{(n)}=x^{(n)}|Y=c_k),k=1,2...,K P(X=x∣Y=ck)=P(X(1)=x(1),...,X(n)=x(n)∣Y=ck),k=1,2...,K
So learn to get the joint probability distribution P ( X , Y ) P(X,Y) P(X,Y).
Conditional probability distribution P ( X = x ∣ Y = c k ) P(X=x|Y=c_k) P(X=x∣Y=ck) There are exponentially many parameters , Its estimation is actually infeasible . in fact , hypothesis x ( j ) x^{(j)} x(j) There are S j S_j Sj individual , j = 1 , 2 , . . . , n j=1,2,...,n j=1,2,...,n, Y Y Y The available values of are K individual , Then the number of parameters is K ∏ n j = 1 S j K\prod_{n}^{j=1}S_j K∏nj=1Sj.
To simplify the calculation , Naive Bayesian algorithm makes the assumption of conditional independence . Conditional independence hypothesis means that the features used for classification are conditionally independent when the category is determined , The formula is as follows : P ( X = x ∣ Y = c k ) = P ( X ( 1 ) = x ( 1 ) , . . . , X ( n ) = x ( n ) ∣ Y = c k ) = ∏ n j = 1 P ( X ( j ) = x ( j ) ∣ Y = c k ) P(X=x|Y=c_k)=P(X^{(1)}=x^{(1)},...,X^{(n)}=x^{(n)}|Y=c_k)=\prod_{n}^{j=1}P(X^{(j)}=x^{(j)}|Y=c_k) P(X=x∣Y=ck)=P(X(1)=x(1),...,X(n)=x(n)∣Y=ck)=n∏j=1P(X(j)=x(j)∣Y=ck)
Naive Bayesian method actually learns the mechanism of generating data , So it belongs to the generation model . The assumption of conditional independence simplifies the computational complexity , But sometimes some classification accuracy will be lost .
Naive Bayes classification , For the given input x x x, The learned model is used to calculate the posterior probability distribution P ( Y = c k ∣ X = x ) P(Y=c_k|X=x) P(Y=ck∣X=x), Take the class with the greatest posterior probability as x x x Class data of . The posterior probability is calculated according to Bayesian theorem : P ( Y = c k ∣ X = x ) = P ( X = x ∣ Y = c k ) P ( Y = c k ) ∑ k P ( X = x ∣ Y = c k ) P ( Y = c k ) P(Y=c_k|X=x)=\frac{P(X=x|Y=c_k)P(Y=c_k)}{\sum_{k}P(X=x|Y=c_k)P(Y=c_k)} P(Y=ck∣X=x)=∑kP(X=x∣Y=ck)P(Y=ck)P(X=x∣Y=ck)P(Y=ck)
therefore , Naive Bayesian classifier can be expressed as :
y = f ( x ) = a r g m a x c k P ( Y = c k ) ∏ j P ( X ( j ) = x ( j ) ∣ Y = c k ) ∑ k P ( Y = c k ) ∏ j P ( X ( j ) = x ( j ) ∣ Y = c k ) y=f(x)=argmax_{c_k}\frac{P(Y=c_k)\prod_{j}P(X^{(j)}=x^{(j)}|Y=c_k)}{\sum_k P(Y=c_k) \prod_{j}{P(X^{(j)}=x^{(j)}|Y=c_k)} } y=f(x)=argmaxck∑kP(Y=ck)∏jP(X(j)=x(j)∣Y=ck)P(Y=ck)∏jP(X(j)=x(j)∣Y=ck)
Be careful , In the upper form , Denominator for all c k c_k ck It's all the same , therefore :
y = f ( x ) = a r g m a x c k P ( Y = c k ) ∏ j P ( X ( j ) = x ( j ) ∣ Y = c k ) y=f(x)=argmax_{c_k}P(Y=c_k)\prod_{j}P(X^{(j)}=x^{(j)}|Y=c_k) y=f(x)=argmaxckP(Y=ck)j∏P(X(j)=x(j)∣Y=ck)
1.2 The meaning of maximizing a posteriori probability
Naive Bayes classifies instances into classes with the largest posterior probability , This is equivalent to minimizing the expected risk . According to the expected risk minimization criterion, a posteriori probability maximization criterion is obtained :
f ( x ) = a r g m a x c k P ( c k ∣ X = x ) f(x)=argmax_{c_k}P(c_k|X=x) f(x)=argmaxckP(ck∣X=x)
That is, the principle of naive Bayesian method .
2. Parameter estimation of naive Bayesian method
2.1 Maximum likelihood estimation
In naive Bayes , Learning means estimating P ( Y = c k ) P(Y=c_k) P(Y=ck) and P ( X ( j ) = x ( j ) ∣ Y = c k ) P(X^{(j)}=x^{(j)}|Y=c_k) P(X(j)=x(j)∣Y=ck). The maximum likelihood estimation method can be used to estimate the corresponding probability . Prior probability P ( Y = c k ) P(Y=c_k) P(Y=ck) The maximum likelihood estimate of is P ( Y = c k ) P(Y=c_k) P(Y=ck) The maximum likelihood estimate of is :
P ( Y = c k ) = ∑ i = 1 N I ( y i = c k ) N , k = 1 , 2 , . . . , K P(Y=c_k)=\frac{\sum_{i=1}^NI(y_i=c_k)}{N},k=1,2,...,K P(Y=ck)=N∑i=1NI(yi=ck),k=1,2,...,K
Set the first j Features x ( j ) x^{(j)} x(j) The set of possible values is a j 1 , a j 2 , . . . , a j S j {a_{j1},a_{j2},...,a_{jS_j}} aj1,aj2,...,ajSj, Conditional probability P ( X ( j ) = a j l ∣ Y = c k ) P(X^{(j)}=a_{jl}|Y=c_k) P(X(j)=ajl∣Y=ck) The maximum likelihood estimate of is :
P ( X j = a j l ∣ Y = c k ) = ∑ i = 1 N I ( x i ( j ) = a j l , y i = c k ) ∑ i = 1 N I ( y i = c k ) P(X^{j}=a_{jl}|Y=c_k)=\frac{\sum_{i=1}^N I(x_i^{(j)}=a_{jl}, y_i=c_k)}{\sum_{i=1}^N I(y_i=c_k)} P(Xj=ajl∣Y=ck)=∑i=1NI(yi=ck)∑i=1NI(xi(j)=ajl,yi=ck)
j = 1 , 2 , . . . , n ; l = 1 , 2 , . . . , S j , k = 1 , 2 , . . . , K j=1,2,...,n; l=1,2,...,S_j, k=1,2,...,K j=1,2,...,n;l=1,2,...,Sj,k=1,2,...,K, x i ( j ) x_i^{(j)} xi(j) It's No i Of samples j Features , a j l a_{jl} ajl It's No j A feature may get the first l It's worth ,I For indicating function .
2.2 Learning and classification algorithms
Algorithm : Naive bayes algorithm (naive Bayes algorithm)
Input : Training data T = ( x 1 , y 2 ) , ( x 2 , y 2 ) , . . . , ( x N , y N ) T={(x_1,y_2),(x_2,y_2),...,(x_N,y_N)} T=(x1,y2),(x2,y2),...,(xN,yN), among x i = ( x i ( 1 ) , x i ( 2 ) , . . . , x i ( n ) ) T x_i=(x_i^{(1)},x_i^{(2)}, ..., x_i^{(n)})^T xi=(xi(1),xi(2),...,xi(n))T, x i ( j ) x_i^{(j)} xi(j) It's No i i i The first sample is j j j Features , x i ( j ) ∈ a j 1 , a j 2 , . . . , a j S x_i^{(j)}\in {a_{j1},a_{j2},...,a_{jS}} xi(j)∈aj1,aj2,...,ajS, a j l a_{jl} ajl It's No j j j A feature may get the first l l l It's worth , j = 1 , 2 , . . . , n j=1,2,...,n j=1,2,...,n, l = 1 , 2 , . . . , S j l=1,2,...,S_j l=1,2,...,Sj, y i ∈ c 1 , c 2 , . . . , c K y_i\in {c_1,c_2,...,c_K} yi∈c1,c2,...,cK; example x x x;
Output : example x x x The classification of :
(1) Calculate prior probability and conditional probability :
P ( Y = c k ) = ∑ i = 1 N I ( y i = c k ) N , k = 1 , 2 , . . . , K P(Y=c_k)=\frac{\sum_{i=1}^N I(y_i=c_k)}{N},k=1,2,...,K P(Y=ck)=N∑i=1NI(yi=ck),k=1,2,...,K
P ( X ( j ) = a j l ∣ Y = c k ) = ∑ i = 1 N I ( x i ( j ) = a j l , y i = c k ) ∑ i = 1 N I ( y i = c k ) , j = 1 , 2 , . . . , n ; I = 1 , 2 , . . . , S j ; k = 1 , 2... , K P(X^{(j)}=a_{jl}|Y=c_k)=\frac{\sum_{i=1}^N I(x_{i}^{(j)}=a_{jl},y_i=c_k)}{\sum_{i=1}^N I(y_i=c_k)}, j=1,2,...,n;I=1,2,...,S_j;k=1,2...,K P(X(j)=ajl∣Y=ck)=∑i=1NI(yi=ck)∑i=1NI(xi(j)=ajl,yi=ck),j=1,2,...,n;I=1,2,...,Sj;k=1,2...,K
(2) For a given instance x = ( x ( 1 ) , x ( 2 ) , . . . , x ( n ) ) T x=(x^{(1)}, x^{(2)}, ..., x^{(n)})^T x=(x(1),x(2),...,x(n))T, Calculation
P ( Y = c k ) ∏ j = 1 n P ( X ( j ) = x ( j ) ∣ Y = c k ) , k = 1 , 2 , . . . , K P(Y=c_k)\prod_{j=1}^{n} P(X^{(j)}=x(j)|Y=c_k), k=1,2,...,K P(Y=ck)j=1∏nP(X(j)=x(j)∣Y=ck),k=1,2,...,K
(3) Identify examples x Class
y = a r g m a x c k P ( Y = c k ) ∏ j = 1 n P ( X ( j ) = x ( j ) ∣ Y = c k ) y=arg max_{c_k}P(Y=c_k)\prod_{j=1}^{n}P(X^{(j)}=x^{(j)}|Y=c_k) y=argmaxckP(Y=ck)j=1∏nP(X(j)=x(j)∣Y=ck)
2.3 Bayesian estimation
The probability value to be estimated is 0 The situation of , This will affect the calculation result of posterior probability , Make the classification deviate . The way to solve this problem is to use Bayesian estimation , In particular , The Bayesian estimation of conditional probability is :
P λ ( X ( j ) = a j l ∣ Y = c k ) = ∑ i = 1 N I ( x i ( j ) = a j l , y i = c k ) + λ ∑ i = 1 N I ( y i = c k ) + S j λ P_\lambda (X^{(j)}=a_{jl}|Y=c_k)=\frac{\sum _{i=1}^N I(x_i^{(j)}=a_{jl}, y_i=c_k)+\lambda }{\sum _{i=1}^N I(y_i=c_k)+S_j\lambda } Pλ(X(j)=ajl∣Y=ck)=∑i=1NI(yi=ck)+Sjλ∑i=1NI(xi(j)=ajl,yi=ck)+λ
among λ ≥ 0 \lambda \ge 0 λ≥0. It is equivalent to giving a positive number to the frequency of each value of a random variable λ > 0 \lambda >0 λ>0. When λ = 0 \lambda =0 λ=0 when , It's maximum likelihood estimation . Constant access λ = 1 \lambda =1 λ=1, This is called Laplacian smoothing (Laplace smoothing). obviously For any l = 1 , 2 , . . . , S j , k = 1 , 2... , K l=1,2,...,S_j, k=1,2...,K l=1,2,...,Sj,k=1,2...,K, Yes
P λ ( X ( j ) = a j l ∣ Y = c k ) > 0 P_\lambda (X^{(j)}=a_{jl}|Y=c_k)>0 Pλ(X(j)=ajl∣Y=ck)>0
∑ l = 1 S j P ( X ( j ) = a j l ∣ Y = c k ) = 1 \sum_{l=1}^{S_j}P(X^{(j)}=a_{jl}|Y=c_k)=1 l=1∑SjP(X(j)=ajl∣Y=ck)=1
Again , The Bayesian estimate of a priori probability is :
P λ ( Y = c k ) = ∑ i = 1 N I ( y i = c k ) + λ N + K λ P_\lambda (Y=c_k)=\frac{\sum_{i=1}^N I(y_i=c_k)+\lambda}{N+K\lambda} Pλ(Y=ck)=N+Kλ∑i=1NI(yi=ck)+λ
3. summary
- Naive Bayes method is a typical generative learning method . The generation method learns the joint probability distribution from the training data P ( X , Y ) P(X,Y) P(X,Y), Then the posterior probability distribution is obtained P ( Y ∣ X ) P(Y|X) P(Y∣X), say concretely , Use training data to learn P ( X ∣ Y ) P(X|Y) P(X∣Y) and P ( Y ) P(Y) P(Y) Estimation , The joint probability distribution is obtained :
P ( X , Y ) = P ( Y ) P ( X ∣ Y ) P(X,Y)=P(Y)P(X|Y) P(X,Y)=P(Y)P(X∣Y)
The probability estimation method can be maximum likelihood estimation or Bayesian estimation - The basic assumption of naive Bayesian method is conditional independence :
P ( X = x ∣ Y − = c k ) = P ( X ( 1 ) = x ( 1 ) , . . . , X ( n ) = x ( n ) ∣ Y = c k ) = ∏ j = 1 n P ( X ( j ) = x ( j ) ∣ Y = c k ) P(X=x|Y-=c_k)=P(X^{(1)=x^{(1)}},...,X^{(n)}=x^{(n)}|Y=c_k)=\prod_{j=1}^{n}P(X^{(j)}=x^{(j)}|Y=c_k) P(X=x∣Y−=ck)=P(X(1)=x(1),...,X(n)=x(n)∣Y=ck)=j=1∏nP(X(j)=x(j)∣Y=ck)
Naive Bayes method is efficient , But the performance of classification is not necessarily very high . - Naive Bayesian method uses Bayesian theorem and learned joint probability model for classification and prediction
P ( Y ∣ X ) = P ( X , Y ) P ( X ) = P ( Y ) P ( X ∣ Y ) ∑ Y P ( Y ) P ( X ∣ Y ) P(Y|X)=\frac{P(X, Y)}{P(X)}=\frac{P(Y)P(X|Y)}{\sum_Y P(Y)P(X|Y)} P(Y∣X)=P(X)P(X,Y)=∑YP(Y)P(X∣Y)P(Y)P(X∣Y)
Enter x To the class with the greatest a posteriori probability y.
y = a r g max c k P ( Y = c k ) ∏ j = 1 n P ( X j = x ( j ) ∣ Y = c k ) y=arg\max_{c_k} P(Y=c_k)\prod_{j=1}^n P(X_j=x^{(j)}|Y=c_k) y=argckmaxP(Y=ck)j=1∏nP(Xj=x(j)∣Y=ck)
The maximum a posteriori probability is equivalent to 0-1 Expected risk minimization in loss function .
边栏推荐
- SQL lab 26~31 summary (subsequent continuous update) (including parameter pollution explanation)
- 静态Vxlan 配置
- Tutorial on principles and applications of database system (007) -- related concepts of database
- About web content security policy directive some test cases specified through meta elements
- Is it safe to open Huatai's account in kainiu in 2022?
- Learning and using vscode
- What is an esp/msr partition and how to create an esp/msr partition
- PowerShell cs-utf-16le code goes online
- Utiliser la pile pour convertir le binaire en décimal
- Realize all, race, allsettled and any of the simple version of promise by yourself
猜你喜欢

爱可可AI前沿推介(7.7)

College entrance examination composition, high-frequency mention of science and Technology
Experiment with a web server that configures its own content
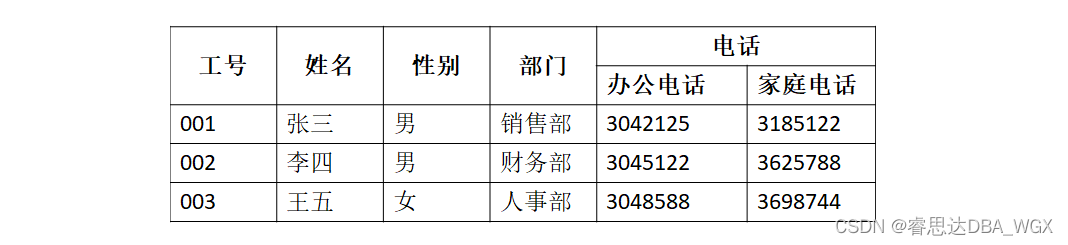
Tutorial on the principle and application of database system (011) -- relational database

wallys/Qualcomm IPQ8072A networking SBC supports dual 10GbE, WiFi 6

The left-hand side of an assignment expression may not be an optional property access.ts(2779)

JS to convert array to tree data
SQL lab 26~31 summary (subsequent continuous update) (including parameter pollution explanation)
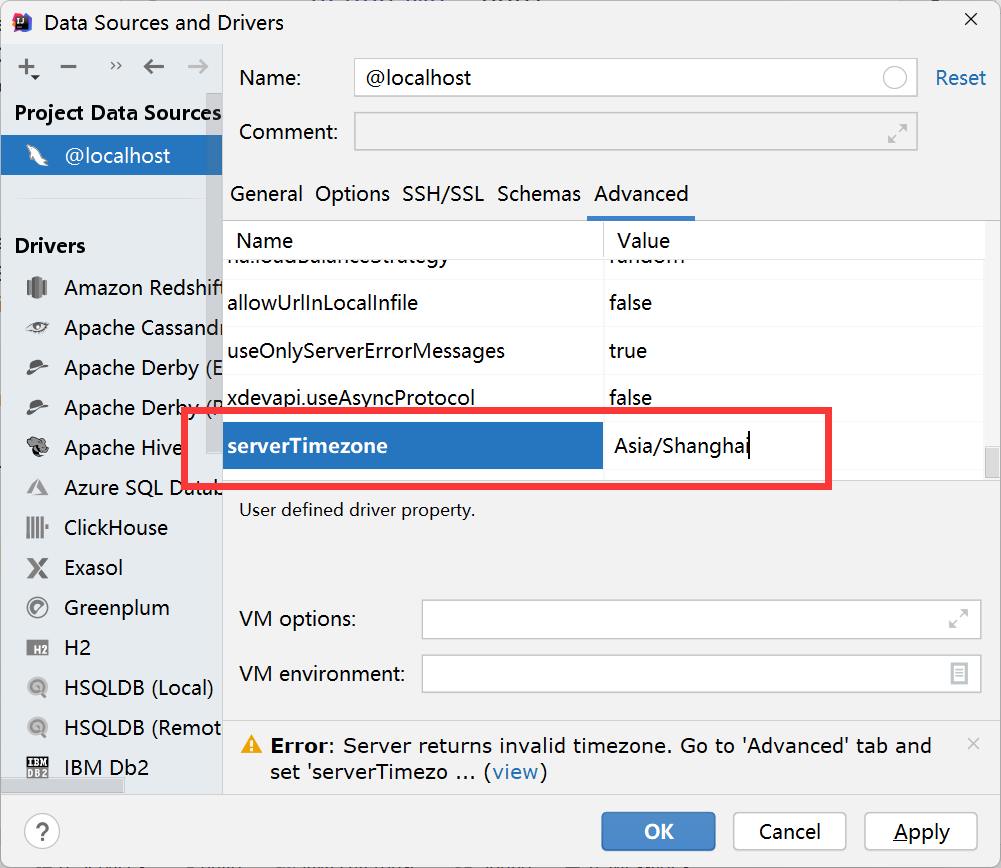
Solve server returns invalid timezone Go to ‘Advanced’ tab and set ‘serverTimezone’ property manually

BGP third experiment report
随机推荐
Sign up now | oar hacker marathon phase III midsummer debut, waiting for you to challenge
千人规模互联网公司研发效能成功之路
Static vxlan configuration
Object. Simple implementation of assign()
数据库系统原理与应用教程(009)—— 概念模型与数据模型
Tutorial on the principle and application of database system (008) -- exercises on database related concepts
The IDM server response shows that you do not have permission to download the solution tutorial
通讯协议设计与实现
BGP actual network configuration
Airserver automatically receives multi screen projection or cross device projection
File upload vulnerability - upload labs (1~2)
免备案服务器会影响网站排名和权重吗?
JS to convert array to tree data
Attack and defense world ----- summary of web knowledge points
When OSPF specifies that the connection type is P2P, it enables devices on both ends that are not in the same subnet to Ping each other
leetcode刷题:二叉树24(二叉树的最近公共祖先)
OSPF exercise Report
gcc 编译报错
Solutions to cross domain problems
SQL lab 21~25 summary (subsequent continuous update) (including secondary injection explanation)