当前位置：网站首页>Leetcode brush questions day49

Leetcode brush questions day49

2022-07-07 17:07:00 【51CTO】

Today's key points — greedy

List of articles

55. Jumping game

Title Description
Thought analysis
Reference code

45. Jumping game II

Title Description
Thought analysis
Reference code

1005. K The maximum array and... After negation

Title Description
Thought analysis
Reference code

55. Jumping game

Title Description

Given an array of nonnegative integers nums , You're in the beginning of the array The first subscript .

Each element in the array represents the maximum length you can jump at that location .

Judge whether you can reach the last subscript .

Example 1：

       
        Input ：nums 
       
       = [
       
       2,
       
       3,
       
       1,
       
       1,
       
       4]
       
        Output ：true
       
        explain ： You can jump first  
       
       1 
       
        Step , From the subscript  
       
       0 
       
        Reach subscript  
       
       1, 
       
        And then from the subscript  
       
       1 
       
        jump  
       
       3
      
1.
2.
3.

Example 2：

       
        Input ：nums 
       
       = [
       
       3,
       
       2,
       
       1,
       
       0,
       
       4]
       
        Output ：false
       
        explain ： No matter what , Always arrive, subscript  
       
       3 
       
        The location of . But the maximum jump length of the subscript is  
       
       0
      
1.
2.
3.

Thought analysis

When I first saw this question, I might think ： If the current location element is 3, What on earth am I doing , Or two steps , Or three steps , How many steps is the best ？

In fact, it doesn't matter how many steps you take , The key is the coverage that can jump ！

In this range , Never mind how you jump , You can jump over anyway .

Then this question turns into whether the jump coverage can cover the end point ！

Take the maximum number of jump steps per move （ Get maximum coverage ）, Every unit moved , Update the maximum coverage .

Greedy algorithm local optimal solution ： Take the maximum number of jump steps each time （ Take the maximum coverage ）, The global optimal solution ： Finally, the overall maximum coverage , See if we can reach the end .

The local optimum leads to the global optimum , No counterexample , Try greed ！

Pictured ：

LeetCode Brush problem day49_i++

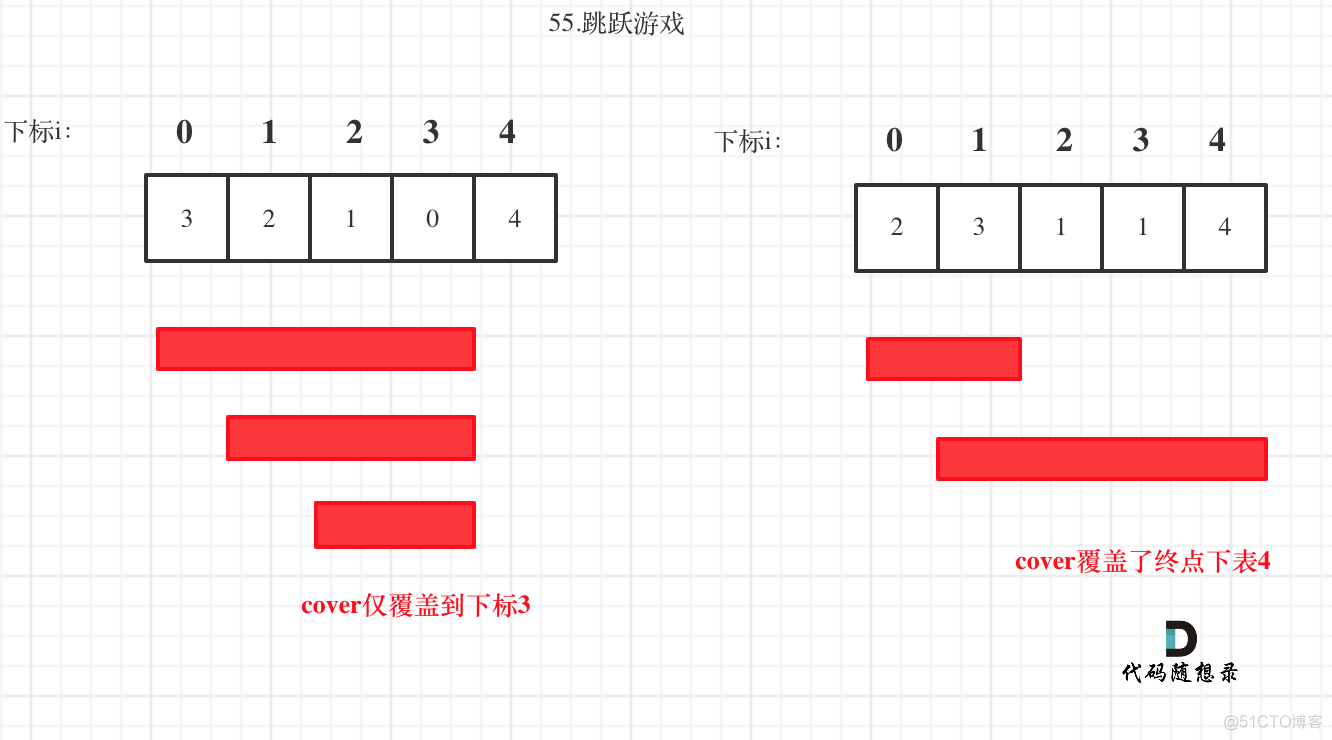
i Each move can only be made in cover Moving within the limits of , Every time you move an element ,cover Get the supplement of the new coverage of this element , Give Way i Keep moving .

and cover Take only max( The range after the value of this element is supplemented , cover Scope of itself ).

If cover Greater than or equal to the end subscript , direct return true That's all right. .

Reference code

       
       #include<bits/stdc++.h>
       
       using 
       
       namespace 
       
       std;
       
       bool 
       
       canJump(
       
       vector
       
       <
       
       int
       
       >& 
       
       nums) { 
       
       int 
       
       cover 
       
       = 
       
       0;
       
       // As far as ( Cover ) The location of 
       
       if(
       
       nums.
       
       size()
       
       ==
       
       1) { 
       
       // Only one element ends directly .
       
       return 
       
       true;
       
  }
       
       for(
       
       int 
       
       i 
       
       = 
       
       0; 
       
       i 
       
       <= 
       
       cover; 
       
       i
       
       ++) {
       
       // The scope is 0-cover, Every jump is in cover Within the scope of  
       
       cover 
       
       = 
       
       max(
       
       nums[
       
       i]
       
       +
       
       i,
       
       cover);
       
       // Find a maximum 
       
       if(
       
       cover
       
       >=
       
       nums.
       
       size()
       
       -
       
       1) {
       
       // end 
       
       return 
       
       true;
       
    }
       
  }
       
       return 
       
       false;
       
       // If the element is traversed cover We haven't reached the last element subscript yet , It is impossible to reach .
       
}
      
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.

45. Jumping game II

Title Description

Here's an array of nonnegative integers nums , You are first in the array .

Each element in the array represents the maximum length you can jump at that location .

Your goal is Use the least number of hops to reach the last position of the array .

Suppose you can always reach the last position of the array .

Example 1:

       
        Input : 
       
       nums 
       
       = [
       
       2,
       
       3,
       
       1,
       
       1,
       
       4]
       
        Output : 
       
       2
       
        explain : 
       
        The minimum number of jumps to the last position is  
       
       2
       
       .
       
        From the subscript for  
       
       0 
       
        Jump to subscript  
       
       1 
       
        The location of , jump  
       
       1 
       
        Step , Then jump  
       
       3
      
1.
2.
3.
4.

Example 2:

Thought analysis

This problem is to calculate the minimum number of steps , Then you have to figure out when the steps must be added by one ？

Greedy thinking , Local optimum ： At present, you can move as much as possible , If you haven't reached the end , Step number plus one . The overall best ： Take as many steps as possible , So as to achieve the minimum number of steps .

Although the idea is like this , But when writing code, you can't really jump far and long , Then you don't know where you can jump the farthest in the next step .

So when you really solve a problem , Start with coverage , No matter how you jump , It must be possible to jump within the coverage , Increase coverage with minimum steps . Once the coverage covers the end point , The result is the minimum number of steps ！

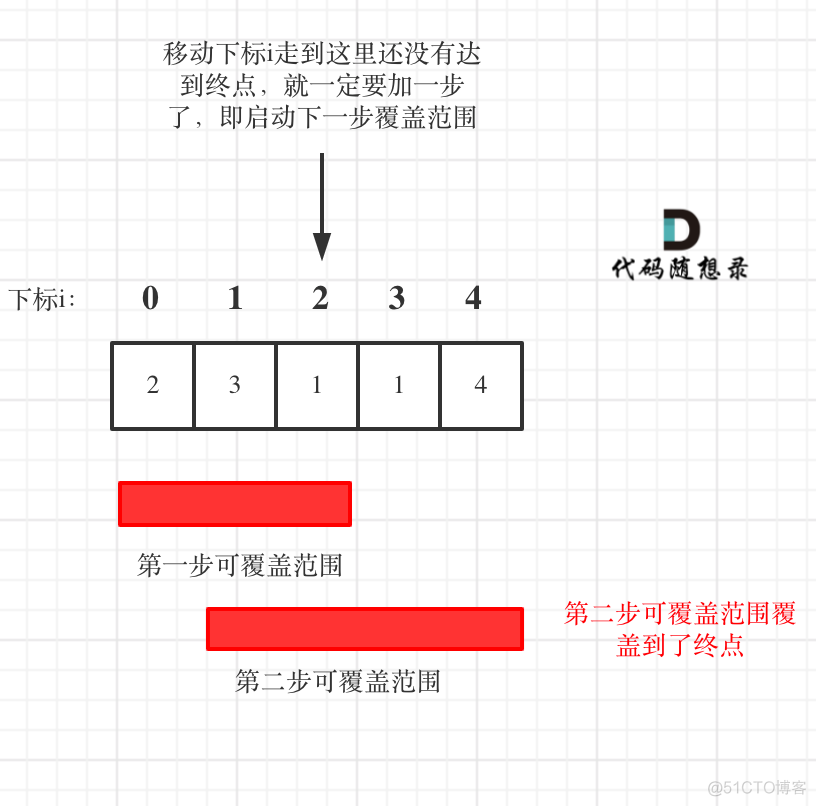
Here we need to count two coverage areas , The maximum coverage of the current step and the maximum coverage of the next step .

If the moving subscript reaches the maximum coverage distance of the current step , If you haven't reached the end , Then we must take another step to increase the coverage , Until the coverage covers the end .

Pictured ：

LeetCode Brush problem day49_i++_02

Reference code

       
       #include<bits/stdc++.h>
       
       using 
       
       namespace 
       
       std;
       
       int 
       
       jump(
       
       vector
       
       <
       
       int
       
       >& 
       
       nums) {
       
       if(
       
       nums.
       
       size()
       
       ==
       
       1){
       
       return 
       
       0;
       
  }
       
       int 
       
       curDistance 
       
       = 
       
       0;
       
       // At present, the farthest   The subscript of the overlay 
       
       int 
       
       nextDistance 
       
       = 
       
       0;
       
       // Next, the subscript of the farthest coverage 
       
       int 
       
       ans 
       
       = 
       
       0;
       
       // Steps taken 
       
       for(
       
       int 
       
       i 
       
       = 
       
       0;
       
       i 
       
       < 
       
       nums.
       
       size(); 
       
       i
       
       ++){
       
       nextDistance 
       
       = 
       
       max(
       
       nums[
       
       i]
       
       +
       
       i,
       
       nextDistance);
       
       // to update nextDistance ( When taking the current step ) 
       
       if(
       
       i
       
       ==
       
       curDistance){
       
       // When equal , It means that you may need to take another step . 
       
       if(
       
       i
       
       !=
       
       nums.
       
       size()
       
       -
       
       1){
       
       // It hasn't arrived yet , Then you must continue to walk  
       
       ans
       
       ++; 
       
       curDistance 
       
       = 
       
       nextDistance;
       
       // Update coverage 
       
       if(
       
       curDistance 
       
       >= 
       
       nums.
       
       size()
       
       -
       
       1) {
       
       // If this new step can reach the end , Then it ends the cycle directly  
       
       break;
       
       // These three lines if Code , It's an optimization , Don't write, just judge at this point .
       
        }
       
      }
       
       else{
       
       // If equal , Then you don't have to go forward . 
       
       break;
       
      } 
       
    }
       
  } 
       
       return 
       
       ans; 
       
}
      
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.

1005. K The maximum array and... After negation

Title Description

Give you an array of integers nums And an integer k , Modify the array as follows ：

Select a subscript i And will nums[i] Replace with -nums[i] .

Repeating this process happens to k Time . You can select the same subscript multiple times i .

After modifying the array in this way , Returns an array of The maximum possible and .

Example 1：

       
        Input ：nums 
       
       = [
       
       4,
       
       2,
       
       3], 
       
       k 
       
       = 
       
       1
       
        Output ：5
       
        explain ： Select subscript  
       
       1 
       
       ,nums 
       
        Turn into  [
       
       4,
       
       -
       
       2,
       
       3]
      
1.
2.
3.

Example 2：

       
        Input ：nums 
       
       = [
       
       3,
       
       -
       
       1,
       
       0,
       
       2], 
       
       k 
       
       = 
       
       3
       
        Output ：6
       
        explain ： Select subscript  (
       
       1, 
       
       2, 
       
       2) 
       
       ,nums 
       
        Turn into  [
       
       3,
       
       1,
       
       0,
       
       2]
      
1.
2.
3.

Example 3：

       
        Input ：nums 
       
       = [
       
       2,
       
       -
       
       3,
       
       -
       
       1,
       
       5,
       
       -
       
       4], 
       
       k 
       
       = 
       
       2
       
        Output ：13
       
        explain ： Select subscript  (
       
       1, 
       
       4) 
       
       ,nums 
       
        Turn into  [
       
       2,
       
       3,
       
       -
       
       1,
       
       5,
       
       4]
      
1.
2.
3.

Thought analysis

Greedy thinking , Local optimum ： Let a negative number with a large absolute value become a positive number , The current value reaches the maximum , The overall best ： The sum of the entire array reaches the maximum .

So if you turn negative numbers into positive numbers ,K Still greater than 0, The problem at this point is a sequence of ordered positive integers , How to change K Secondary positive and negative , Give Way Array and Maximum .

Then it's another greedy ： Local optimum ： Only find the positive integer with the smallest value for inversion , The current value can reach the maximum （ For example, an array of positive integers {5, 3, 1}, reverse 1 obtain -1 Than reverse 5 Got -5 Mostly ）, The best in the world ： Whole Array and Maximum .

Then the steps to solve this problem are ：

First step ： Sort the array according to the absolute value size from large to small , Pay attention to the size of the absolute value
The second step ： Traverse back and forth , When you encounter a negative number, change it to a positive number , meanwhile K–
The third step ： If K Greater than 0, Then repeatedly change the element with the lowest value , take K run out
Step four ： Sum up

Reference code

       
       #include<bits/stdc++.h>
       
       using 
       
       namespace 
       
       std;
       
       static 
       
       bool 
       
       cmp(
       
       int 
       
       a,
       
       int 
       
       b){
       
       // The one with the largest absolute value is in the front  
       
       return 
       
       abs(
       
       a) 
       
       > 
       
       abs(
       
       b);
       
}
       
       int 
       
       largestSumAfterKNegations(
       
       vector
       
       <
       
       int
       
       >& 
       
       nums, 
       
       int 
       
       k) {
       
       int 
       
       ans 
       
       = 
       
       0;
       
       sort(
       
       nums.
       
       begin(),
       
       nums.
       
       end());
       
       for(
       
       int 
       
       i 
       
       = 
       
       0; 
       
       i 
       
       < 
       
       nums.
       
       size(); 
       
       i
       
       ++){
       
       if(
       
       nums[
       
       i] 
       
       < 
       
       0 
       
       && 
       
       k 
       
       > 
       
       0) {
       
       nums[
       
       i]
       
       *=-
       
       1;
       
       k
       
       --;
       
    }
       
  }
       
       if(
       
       k 
       
       % 
       
       2 
       
       == 
       
       1){ 
       
       // If k There's more left , Just choose the smallest number   Over and over again *-1, until k Just use it up 
       
       nums[
       
       nums.
       
       size()
       
       -
       
       1] 
       
       *= 
       
       -
       
       1;
       
  }
       
       for(
       
       int 
       
       i 
       
       = 
       
       0; 
       
       i 
       
       < 
       
       nums.
       
       size(); 
       
       i
       
       ++){
       
       ans 
       
       += 
       
       nums[
       
       i];
       
  }
       
       return 
       
       ans;
       
}
      
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.

If there is harvest ！！！ I hope the old fellow will have three links. , give the thumbs-up 、 Collection 、 forward .
It's not easy to create , Don't forget to like it , More people can see this article , By the way, encourage me to write a better blog

原网站

版权声明
本文为[51CTO]所创，转载请带上原文链接，感谢
https://yzsam.com/2022/188/202207071533116395.html