当前位置:网站首页>Mathematics in machine learning -- common probability distribution (XIII): Logistic Distribution
Mathematics in machine learning -- common probability distribution (XIII): Logistic Distribution
2022-07-06 18:39:00 【von Neumann】
Catalogues :《 Mathematics in machine learning 》 General catalogue
Related articles :
· Common probability distribution ( One ): Bernoulli distribution (Bernoulli Distribution )
· Common probability distribution ( Two ): Category distribution (Multinoulli Distribution )
· Common probability distribution ( 3、 ... and ): The binomial distribution (Binomial Distribution )
· Common probability distribution ( Four ): Uniform distribution (Uniform Distribution )
· Common probability distribution ( 5、 ... and ): Gaussian distribution (Gaussian Distribution )/ Normal distribution (Normal Distribution )
· Common probability distribution ( 6、 ... and ): An index distribution (Exponential Distribution )
· Common probability distribution ( 7、 ... and ): Laplacian distribution (Laplace Distribution )
· Common probability distribution ( 8、 ... and ): Dirac distribution (Dirac Distribution )
· Common probability distribution ( Nine ): Empirical distribution (Empirical Distribution )
· Common probability distribution ( Ten ): Beta distribution (Beta Distribution )
· Common probability distribution ( 11、 ... and ): Dirichlet distribution (Dirichlet Distribution )
· Common probability distribution ( Twelve ): Structured probability model / Graph model
· Common probability distribution ( 13、 ... and ): Logistic distribution (Logistic Distribution )
set up X X X It's a continuous random variable , X X X Obey the logistic distribution (Logistic Distribution ) Refer to X X X It has the following distribution function and density function :
F ( x ) = P ( X ≤ x ) = 1 1 + e − ( x − μ ) γ F(x)=P(X\leq x)=\frac{1}{1+e^{-\frac{(x-\mu)}{\gamma}}} F(x)=P(X≤x)=1+e−γ(x−μ)1
f ( x ) = F ′ ( x ) = e − ( x − μ ) γ γ ( 1 + e − ( x − μ ) γ ) 2 f(x)=F'(x)=\frac{e^{-\frac{(x-\mu)}{\gamma}}}{\gamma(1+e^{-\frac{(x-\mu)}{\gamma}})^2} f(x)=F′(x)=γ(1+e−γ(x−μ))2e−γ(x−μ)
among , μ \mu μ For position parameters , γ > 0 \gamma>0 γ>0 For shape parameters .
Density function of logistic distribution f ( x ) f(x) f(x) And distribution function F ( x ) F(x) F(x) The figure of is shown in the figure below . The distribution function belongs to the logical tearing function , The graph is a S Shape curve (sigmoid curve). The curve is in point ( μ , 1 2 ) (\mu,\frac{1}{2}) (μ,21) It's central symmetry , The meet
F ( − x + μ ) − 1 2 = − F ( x − μ ) + 1 2 F(-x+\mu)-\frac{1}{2}=-F(x-\mu)+\frac{1}{2} F(−x+μ)−21=−F(x−μ)+21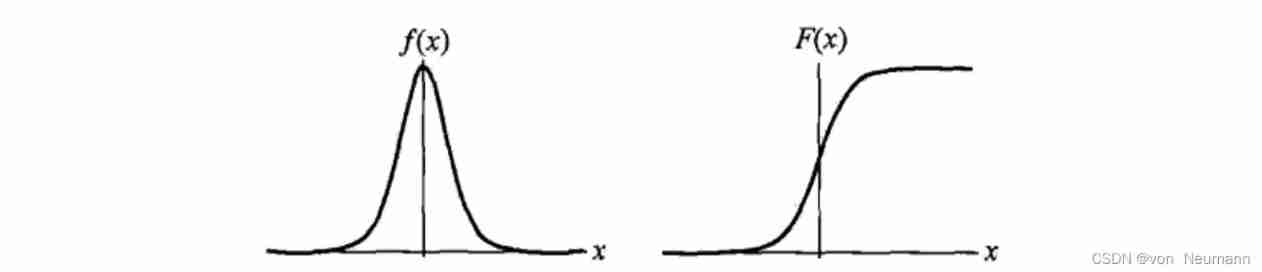
The curve grows faster near the center , Slow growth at both ends . shape parameter γ \gamma γ The smaller the value of , The faster the curve grows near the center .
边栏推荐
- Cobra quick start - designed for command line programs
- Recommend easy-to-use backstage management scaffolding, everyone open source
- C语言自动预订飞机票问题
- atcoder它A Mountaineer
- With the implementation of MapReduce job de emphasis, a variety of output folders
- UDP协议:因性善而简单,难免碰到“城会玩”
- 2022暑期项目实训(二)
- Stm32+esp8266+mqtt protocol connects onenet IOT platform
- 用友OA漏洞学习——NCFindWeb 目录遍历漏洞
- echart简单组件封装
猜你喜欢
关于npm install 报错问题 error 1

视频化全链路智能上云?一文详解什么是阿里云视频云「智能媒体生产」
Distiller les connaissances du modèle interactif! L'Université de technologie de Chine & meituan propose Virt, qui a à la fois l'efficacité du modèle à deux tours et la performance du modèle interacti
Execution process of MySQL query request - underlying principle
二叉搜索树
传输层 拥塞控制-慢开始和拥塞避免 快重传 快恢复
Windows connects redis installed on Linux

Blue Bridge Cup real question: one question with clear code, master three codes
Maixll-Dock 摄像头使用
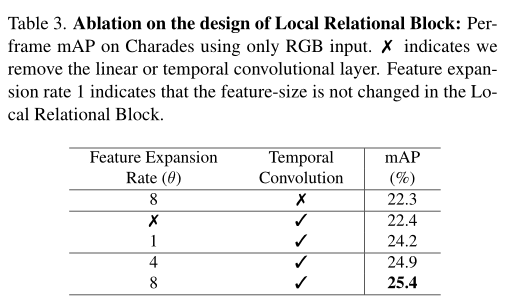
Ms-tct: INRIA & SBU proposed a multi-scale time transformer for motion detection. The effect is SOTA! Open source! (CVPR2022)...
随机推荐
There is a sound prompt when inserting a USB flash disk under win10 system, but the drive letter is not displayed
This article discusses the memory layout of objects in the JVM, as well as the principle and application of memory alignment and compression pointer
Penetration test information collection - basic enterprise information
Penetration test information collection - App information
celery最佳实践
Shangsilicon Valley JUC high concurrency programming learning notes (3) multi thread lock
Specify flume introduction, installation and configuration
POJ 2208 已知边四面体六个长度,计算体积
2022暑期项目实训(三)
Self supervised heterogeneous graph neural network with CO comparative learning
Markdown syntax for document editing (typera)
首先看K一个难看的数字
Windows connects redis installed on Linux
C language exchanges two numbers through pointers
287. Find duplicates
[Sun Yat sen University] information sharing of postgraduate entrance examination and re examination
UFIDA OA vulnerability learning - ncfindweb directory traversal vulnerability
简单易用的PDF转SVG程序
Brief description of SQL optimization problems
DOM简要