当前位置:网站首页>[statistical learning method] learning notes - support vector machine (Part 2)
[statistical learning method] learning notes - support vector machine (Part 2)
2022-07-07 12:34:00 【Sickle leek】
Statistical learning methods learning notes —— Support vector machine ( Next )
3. Nonlinear support vector machine and kernel function
Nonlinear support vector machines , Its main feature is the use of nuclear technology (kernel trick).
3.1 Nuclear skills
- Nonlinear classification problem 、
Nonlinear classification problem refers to the problem that can be well classified by using nonlinear models .
Generally speaking , For a given training data set T = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x N , y N ) } T=\{(x_1, y_1), (x_2, y_2), ..., (x_N, y_N)\} T={ (x1,y1),(x2,y2),...,(xN,yN)}, among , example x i x_i xi Belongs to input space , x i ∈ X = R n x_i\in \mathcal{X}=R^n xi∈X=Rn, There are two corresponding class tags y i ∈ y = { − 1 , + 1 } , i = 1 , 2 , . . . , N y_i\in \mathcal{y}=\{-1, +1\}, i=1,2,...,N yi∈y={ −1,+1},i=1,2,...,N. If it works R n R^n Rn One of themHypersurfaceDivide the positive and negative examples correctly , Call this problemNonlinear separable problems.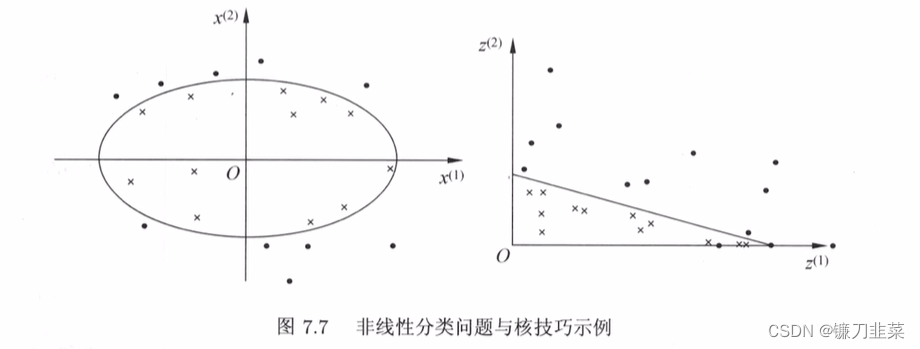
The classification problem of the left graph cannot be solved by using straight lines ( Linear model ) Separate positive and negative instances correctly , But you can use an elliptic curve ( Nonlinear models ) Separate them correctly .
If you can use a hypersurface to correctly separate positive and negative examples , This problem is called a nonlinear separable problem . Nonlinear problems are often difficult to solve , So I hope to solve this problem by solving the linear classification problem . The method adopted is a nonlinear transformation , Transform nonlinear problems into linear problems . Solve the original problem by solving the linear problem .
Let the original space be X ⊂ R 2 , x = ( x ( 1 ) , x ( 2 ) ) T ∈ X \mathcal{X}⊂R^2,x=(x^{(1)},x^{(2)})^T\in \mathcal{X} X⊂R2,x=(x(1),x(2))T∈X, The new space is Z ⊂ R 2 \mathcal{Z}⊂R^2 Z⊂R2, z = ( z ( 1 ) , z ( 2 ) ) T ∈ Z z=(z^{(1)},z^{(2)})^T∈\mathcal{Z} z=(z(1),z(2))T∈Z, Define the mapping from the original space to the new space : z = ϕ ( x ) = ( ( x ( 1 ) ) 2 , ( x ( 2 ) ) 2 ) T z=ϕ(x)=((x^{(1)})^2,(x^{(2)})^2)^T z=ϕ(x)=((x(1))2,(x(2))2)T
Then the ellipse of the original space w 1 ( x ( 1 ) ) 2 + w 2 ( x ( 2 ) ) 2 + b = 0 w_1(x^{(1)})^2+w_2(x^{(2)})^2+b=0 w1(x(1))2+w2(x(2))2+b=0
Transform into a straight line in the new space w 1 z ( 1 ) + w 2 z ( 2 ) + b = 0 w_1z^{(1)}+w_2z^{(2)}+b=0 w1z(1)+w2z(2)+b=0
Nuclear techniques are applied to SVM, The basic idea is to input space through a nonlinear transformation ( European space R n R^n Rn Or discrete sets ) Corresponding to a feature space ( Hilbert space H \mathcal{H} H), Make the input space R n R^n Rn The hypercurved surface in corresponds to the feature space H \mathcal{H} H Hyperplane model of ( Support vector machine ). such , The learning task of classification problem is to solve linear in feature space SVM You can do it .
- Definition of kernel function

The idea of nuclear technology is , Only kernel functions are defined in learning and prediction K ( x , z ) K(x,z) K(x,z), Instead of the definition mapping function shown ϕ ϕ ϕ. adopt , Direct calculation K ( x , z ) K(x,z) K(x,z) Relatively easy , And by ϕ ( x ) ϕ(x) ϕ(x) and ϕ ( z ) ϕ(z) ϕ(z) Calculation K ( x , z ) K(x,z) K(x,z) Not easy . The feature space H \mathcal{H} H It's usually high dimensional , Even infinite dimensional .
For a given core K ( x , z ) K(x,z) K(x,z), The feature space H \mathcal{H} H And mapping functions ϕ ϕ ϕ The choice of is not unique , You can take different feature spaces , Even in the same feature space, different mappings can be taken .
- The application of kernel technique in support vector machine
In the dual problem of linear support vector machine , Whether it is an objective function or a decision function ( Separating hyperplanes ) Only the inner product between the input instance and the instance is involved . Inner product in objective function of dual problem x i ⋅ x j x_i\cdot x_j xi⋅xj You can use kernel functions K ( x i , x j ) = ϕ ( x i ) ⋅ ϕ ( x j ) K(x_i, x_j)=ϕ(x_i) \cdot ϕ(x_j) K(xi,xj)=ϕ(xi)⋅ϕ(xj) Instead of . In this case, the objective function of the dual problem becomes : W ( α ) = 1 2 ∑ i = 1 N ∑ j = 1 N α i α j y i y j K ( x i , x j ) − ∑ i = 1 N α i W(\alpha)=\frac{1}{2}\sum_{i=1}^N\sum_{j=1}^N \alpha_i\alpha_j y_i y_j K(x_i ,x_j)-\sum_{i=1}^N\alpha_i W(α)=21i=1∑Nj=1∑NαiαjyiyjK(xi,xj)−i=1∑Nαi
Again , The inner product in the separation decision function can also be replaced by kernel function , The classification decision function becomes f ( x ) = s i g n ( ∑ i = 1 N s α i ∗ y i ϕ ( x i ) ⋅ ϕ ( x ) + b ∗ ) = s i g n ( ∑ i = 1 N s α i ∗ y i K ( x i , x ) + b ∗ ) f(x)=sign(\sum_{i=1}^{N_s} \alpha_i^* y_i \phi (x_i) \cdot \phi(x)+b^*)=sign(\sum_{i=1}^{N_s}\alpha_i^* y_i K(x_i, x)+b^*) f(x)=sign(i=1∑Nsαi∗yiϕ(xi)⋅ϕ(x)+b∗)=sign(i=1∑Nsαi∗yiK(xi,x)+b∗)
Learn linearity from training samples in the new feature space SVM. Learning is implicit in the feature space , There is no need to explicitly define feature space and mapping function . Such a technique is called the nuclear technique . When the mapping function is nonlinear , Learned that contains kernel function SVM It is a nonlinear classification model .
in application , Often rely on domain knowledge to directly select kernel function , The validity of kernel function needs to be verified by experiments .
3.2 Positive determination
function K ( x , z ) K(x,z) K(x,z) What conditions can be satisfied to be called a kernel function ? Generally speaking, the kernel function is a positive definite kernel function (positive definite kernel function). First, introduce some preliminary knowledge .
hypothesis K ( x , z ) K(x, z) K(x,z) Is defined in X × X \mathcal{X} \times \mathcal{X} X×X Symmetric functions on , And for any x 1 , x 2 , . . . , x m ∈ X x_1, x_2, ..., x_m\in \mathcal{X} x1,x2,...,xm∈X, K ( x , z ) K(x, z) K(x,z) About x 1 , x 2 , . . . , x m x_1, x_2, ..., x_m x1,x2,...,xm Of Gram The matrix is positive semidefinite . According to the function K ( x , z ) K(x, z) K(x,z), Form a Hilbert space , The step is : First define the mapping ϕ \phi ϕ And form a vector space S \mathcal{S} S; And then in S \mathcal{S} S Define inner product on to form inner product space ; The final will be S \mathcal{S} S Completion constitutes Hilbert space .
Define mapping , Form vector space S \mathcal{S} S
First define the mapping ϕ : x → K ( ⋅ , x ) \phi: x \rightarrow K(\cdot , x) ϕ:x→K(⋅,x)
According to this mapping , To any x i ∈ X , α i ∈ R , i = 1 , 2 , . . . , m x_i \in \mathcal{X}, \alpha_i \in R, i=1,2,...,m xi∈X,αi∈R,i=1,2,...,m, Define linear combinations f ( ⋅ ) = ∑ i = 1 m α i K ( ⋅ , x i ) f(\cdot) = \sum_{i=1}^m \alpha_i K(\cdot , x_i) f(⋅)=i=1∑mαiK(⋅,xi) Consider a set of elements from linear combinations S \mathcal{S} S. Because of the set S \mathcal{S} S Addition and multiplication operations are closed , therefore S \mathcal{S} S Form a vector space .stay S \mathcal{S} S Define inner product on , Make it an inner product space
stay S \mathcal{S} S Define an operation on ∗ * ∗: To any f , g ∈ S f, g\in \mathcal{S} f,g∈S, f ( ⋅ ) = ∑ i = 1 m α i K ( ⋅ , x i ) f(\cdot) = \sum_{i=1}^m \alpha_i K(\cdot, x_i) f(⋅)=i=1∑mαiK(⋅,xi) g ( ⋅ ) = ∑ j = 1 l β j K ( ⋅ , z j ) g(\cdot) = \sum_{j=1}^l \beta_j K(\cdot, z_j) g(⋅)=j=1∑lβjK(⋅,zj) Define operations ∗ * ∗
f ∗ g = ∑ i = 1 m ∑ j = 1 l α i β j K ( x i , z j ) f * g=\sum_{i=1}^m \sum_{j=1}^l \alpha_i \beta_j K(x_i, z_j) f∗g=i=1∑mj=1∑lαiβjK(xi,zj)The inner product space S \mathcal{S} S Complete into Hilbert space
Now let's take the inner product space S \mathcal{S} S Completeness , The norm can be obtained from the inner product defined by the above formula ∣ ∣ f ∣ ∣ = f ⋅ f ||f||=\sqrt{f\cdot f} ∣∣f∣∣=f⋅f
therefore , S \mathcal{S} S Is a normed vector space . According to the theory of functional analysis , For incomplete normed vector spaces S \mathcal{S} S, It must be complete , Get a complete normed vector space H \mathcal{H} H. An inner product space , When a normed vector space is complete , It's Hilbert space . such , Then we get Hilbert space H \mathcal{H} H.
This Hilbert space H \mathcal{H} H It is called reproducing kernel Hilbert space . This is due to nuclear K Regenerative , The meet K ( ⋅ , x ) ⋅ f = f ( x ) K(\cdot, x) \cdot f = f(x) K(⋅,x)⋅f=f(x) And K ( ⋅ , x ) ⋅ K ( ⋅ , z ) = K ( x , z ) K(\cdot, x)\cdot K(\cdot, z)=K(x, z) K(⋅,x)⋅K(⋅,z)=K(x,z)
It is called regenerative nucleus .
- A necessary and sufficient condition for a positive definite kernel
Theorem : A necessary and sufficient condition for a positive definite kernel : set up K : X × X → R K: \mathcal{X}\times \mathcal{X} \rightarrow R K:X×X→R It's a symmetric function , be K ( x , z ) K(x, z) K(x,z) The necessary and sufficient condition for a positive definite kernel function is for any x i i n X , i = 1 , 2 , . . . , m , K ( x , z ) x_i\ in \mathcal{X}, i=1,2,...,m, K(x,z) xi inX,i=1,2,...,m,K(x,z) Corresponding Gram matrix :
K = [ K ( x i , x j ) ] m × n K = [K(x_i, x_j)]_{m\times n} K=[K(xi,xj)]m×n
It's a positive semidefinite matrix .
Definition : Equivalent definition of positive definite kernel : set up X ⊂ R 2 , K ( x , z ) \mathcal{X} ⊂R^2, K(x, z) X⊂R2,K(x,z) Is defined in KaTeX parse error: Undefined control sequence: \tims at position 13: \mathcal{X} \̲t̲i̲m̲s̲ ̲\mathcal{X} Symmetric functions on , If for any x i ∈ X , i = 1 , 2 , . . . , m , K ( x , z ) x_i \in \mathcal{X}, i=1,2,..., m, K(x,z) xi∈X,i=1,2,...,m,K(x,z) Corresponding Gram matrix
K = [ K ( x i , x j ) ] m × n K = [K(x_i, x_j)]_{m\times n} K=[K(xi,xj)]m×n
It's a positive semidefinite matrix , said K ( x , z ) K(x, z) K(x,z) It's positive .
3.3 Common kernel functions
(1) Polynomial kernel function (polynomial kernel function)
K ( x , z ) = ( x ⋅ z + 1 ) p K(x,z)=(x\cdot z+1)^p K(x,z)=(x⋅z+1)p
The corresponding support vector machine is a p Polynomials classifier . In this case , The classification decision function becomes
f ( x ) = s i g n ( ∑ i = 1 N s α i ∗ y i ( x i ⋅ x + 1 ) p + b ∗ ) f(x)=sign(\sum_{i=1}^{N_s}α_i^*y_i(x_i\cdot x+1)^p+b^∗) f(x)=sign(i=1∑Nsαi∗yi(xi⋅x+1)p+b∗)
(2) Gaussian kernel (Gaussian kernel function)
K ( x , z ) = e x p ( − ∣ ∣ x − z ∣ ∣ 2 2 σ 2 ) K(x,z)=exp(−\frac{||x−z||^2}{2σ^2}) K(x,z)=exp(−2σ2∣∣x−z∣∣2)
The corresponding support vector machine is Gaussian radial basis function classifier . In this case , The classification decision function becomes
f ( x ) = s i g n ( ∑ i = 1 N s α i ∗ y i e x p ( − ∣ ∣ x − z ∣ ∣ 2 2 σ 2 ) + b ∗ ) f(x)=sign(\sum_{i=1}{N_s}α_i^*y_i exp(−\frac{||x−z||^2}{2σ^2})+b^∗) f(x)=sign(i=1∑Nsαi∗yiexp(−2σ2∣∣x−z∣∣2)+b∗)
(3) String kernel function
Kernel functions can be defined not only in Euclidean space , It can also be defined on the set of discrete data . such as , String kernel is the kernel function defined on string set . String kernel function in text classification , Information retrieval , Biological information and other aspects have applications .
Judgement kernel function
(1) Given a kernel function K K K, about a > 0 a>0 a>0, a K aK aK Also known as kernel function .
(2) Given two kernel functions K ′ K′ K′ and K ′ ′ K′′ K′′, K ′ K ′ ′ K′K′′ K′K′′ Also known as kernel function .
(3) For any real valued function in the input space f ( x ) f(x) f(x), K ( x 1 , x 2 ) = f ( x 1 ) f ( x 2 ) K(x_1,x_2)=f(x_1)f(x_2) K(x1,x2)=f(x1)f(x2) It's a kernel function .
3.4 Nonlinear support vector machines
Definition : Nonlinear support vector machines : From the nonlinear classification training set , Maximization through kernel function and soft interval , Or convex quadratic programming , Learning the classification decision function f ( x ) = s i g n ( ∑ i = 1 N α i ∗ y i K ( x , x i ) + b ∗ ) f(x)=sign(\sum_{i=1}^N \alpha_i^* y_i K(x, x_i)+b^*) f(x)=sign(i=1∑Nαi∗yiK(x,xi)+b∗) It is called nonlinear support vector machine , K ( x , z ) K(x,z) K(x,z) It's a positive definite kernel function .
Algorithm : Nonlinear support vector machine learning algorithm
Input : Training data set T = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x N , y N ) } T=\{(x_1, y_1), (x_2, y_2), ..., (x_N, y_N)\} T={ (x1,y1),(x2,y2),...,(xN,yN)}, among , x i ∈ X = R n x_i\in \mathcal{X}=R^n xi∈X=Rn, y i ∈ y = { − 1 , + 1 } , i = 1 , 2 , . . . , N y_i\in \mathcal{y}=\{-1, +1\}, i=1,2,...,N yi∈y={ −1,+1},i=1,2,...,N;
Output : Classification decision function
(1) Select the appropriate kernel function K ( x , z ) K(x,z) K(x,z) And the appropriate parameters C, Construct and solve optimization problems
min α 1 2 ∑ i = 1 N ∑ j = 1 N α i α j y i y j K ( x i , x j ) − ∑ i = 1 N α i \min_\alpha \frac{1}{2} \sum_{i=1}^N \sum_{j=1}^N \alpha_i \alpha_j y_i y_j K(x_i, x_j) - \sum_{i=1}^N \alpha_i αmin21i=1∑Nj=1∑NαiαjyiyjK(xi,xj)−i=1∑Nαi
s . t . ∑ i = 1 N α i y i = 0 , 0 ≤ α i ≤ C , i = 1 , 2 , . . . , N s.t. \ \sum_{i=1}^N \alpha_i y_i = 0, 0\le \alpha_i \le C, i=1,2,..., N s.t. i=1∑Nαiyi=0,0≤αi≤C,i=1,2,...,N
Find the optimal solution α ∗ = ( α 1 ∗ , α 2 ∗ , . . . , α N ∗ ) T \alpha^* = (\alpha_1^*, \alpha_2^*, ..., \alpha_N^*)^T α∗=(α1∗,α2∗,...,αN∗)T.
(2) choice α ∗ \alpha^* α∗ A component of α j ∗ \alpha_j^* αj∗ Suitable conditions 0 < α j ∗ < C 0< \alpha_j^* < C 0<αj∗<C, Calculation b ∗ = y j − ∑ i = 1 N y i α i ∗ y i K ( x i ⋅ x j ) b^*=y^j-\sum_{i=1}^Ny_i\alpha_i^*y_iK(x_i \cdot x_j) b∗=yj−∑i=1Nyiαi∗yiK(xi⋅xj)
(3) Construct decision function :
f ( x ) = s i g n ( ∑ i = 1 N α i ∗ y i K ( x ⋅ x i ) + b ∗ ) f(x)=sign(\sum_{i=1}^N \alpha_i^* y_i K(x\cdot x_i) + b^*) f(x)=sign(i=1∑Nαi∗yiK(x⋅xi)+b∗)
When K ( x , z ) K(x, z) K(x,z) Is a positive definite kernel function , The above process is to solve the convex quadratic programming problem , Solutions exist .
4. Sequence minimum optimization algorithm
SMO Algorithm : How to realize support vector machine learning efficiently , Is a heuristic algorithm , The basic idea is :
If the solutions of the variables satisfy the optimization problem KKT Conditions (Karush-Kuhn-Tucker conditions), Then the solution of this optimization problem is obtained . because KKT The condition is a necessary and sufficient condition for the optimization problem . otherwise , Choose two variables , Fix other variables , In view of these two variables, a quadratic programming problem is constructed .
4.1 A method for solving quadratic programming with two variables
In order to solve the quadratic programming problem with two variables , First, analyze the constraints , Then we find the minimum under this constraint .
4.2 How to choose variables
SMO The algorithm selects two variables in each subproblem to optimize , At least one of these variables is a violation of KKT Conditions of the .
(1) The choice of the first variable
SMO Say choose the second 1 The process of variables is an outer loop , The outer loop is selected from the training samples KKT The most severe sample point , And take its corresponding variable as the second 1 A variable .
(2) The first 2 Choice of variables
SMO Say choose the second 2 The process of two variables is an inner loop . Suppose we have found the second... In the outer cycle 1 A variable a 1 a_1 a1, Now we have to find the second... In the inner loop 2 A variable a 2 a_2 a2. The first 2 The selection criteria of variables is to make a 2 a_2 a2 There is enough change .
(3) Calculate the threshold b b b And the difference E i E_i Ei
After each optimization of two variables , Recalculate the threshold b. After optimizing two variables at a time , The corresponding... Must also be updated E i E_i Ei value , And save them in the list .
4.3 SMO Algorithm

summary
- The simplest case of support vector machine is linear separable support vector machine , Or hard interval support vector machine . The condition of constructing it is that the training data is linearly separable . The learning strategy is the maximum interval method .
- In reality, there are few cases of linear separability when training data sets , Training sets are often approximately linearly separable , In this case, linear support vector machine , Or soft interval support vector machine . Linear support vector machine is the most basic support vector machine .
- For nonlinear classification problems in input space , It can be transformed into a linear classification problem in a high-dimensional feature space by nonlinear transformation , Learning support vector machines in high-dimensional feature space . Because in the dual problem of learning linear support vector machines , The objective function and classification decision function only involve the inner product between instances , So there is no need to explicitly specify the nonlinear transformation , Instead, we replace the inner product with a kernel function . The kernel function represents , Through the inner product between two instances after a nonlinear transformation .
- SMO The algorithm is a fast learning algorithm of support vector machine , Its characteristic is that the original quadratic programming problem is continuously decomposed into two variable quadratic programming subproblems , The sub problem is solved analytically , Until all variables satisfy KKT Until the conditions are met , In this way, the optimal solution of the original quadratic programming problem is obtained by heuristic method .
Content sources
[1] 《 Statistical learning method 》 expericnce
[2] https://blog.csdn.net/qq_42794545/article/details/121080091
边栏推荐
- Solutions to cross domain problems
- (to be deleted later) yyds, paid academic resources, please keep a low profile!
- [pytorch practice] image description -- let neural network read pictures and tell stories
- Several methods of checking JS to judge empty objects
- What is an esp/msr partition and how to create an esp/msr partition
- 爱可可AI前沿推介(7.7)
- How much does it cost to develop a small program mall?
- idm服务器响应显示您没有权限下载解决教程
- [play RT thread] RT thread Studio - key control motor forward and reverse rotation, buzzer
- Pule frog small 5D movie equipment | 5D movie dynamic movie experience hall | VR scenic area cinema equipment
猜你喜欢
Configure an encrypted web server
Introduction and application of smoothstep in unity: optimization of dissolution effect

wallys/Qualcomm IPQ8072A networking SBC supports dual 10GbE, WiFi 6
Several methods of checking JS to judge empty objects

BGP third experiment report
About web content security policy directive some test cases specified through meta elements

普乐蛙小型5d电影设备|5d电影动感电影体验馆|VR景区影院设备
leetcode刷题:二叉树26(二叉搜索树中的插入操作)
leetcode刷题:二叉树22(二叉搜索树的最小绝对差)
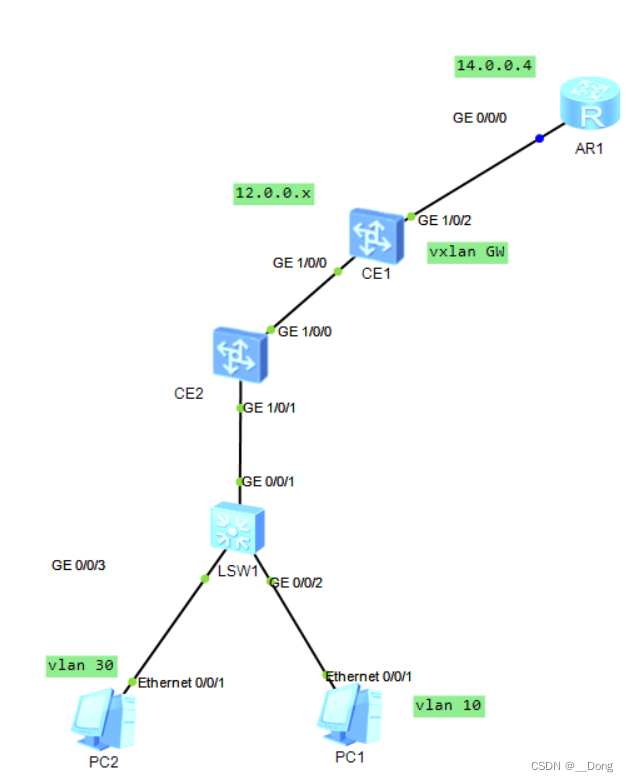
Vxlan static centralized gateway
随机推荐
【统计学习方法】学习笔记——第四章:朴素贝叶斯法
Upgrade from a tool to a solution, and the new site with praise points to new value
The left-hand side of an assignment expression may not be an optional property access. ts(2779)
Sign up now | oar hacker marathon phase III midsummer debut, waiting for you to challenge
Configure an encrypted web server
Error in compiling libssl
即刻报名|飞桨黑客马拉松第三期盛夏登场,等你挑战
BGP third experiment report
【统计学习方法】学习笔记——提升方法
ES底层原理之倒排索引
数据库系统原理与应用教程(011)—— 关系数据库
Session
全球首堆“玲龙一号”反应堆厂房钢制安全壳上部筒体吊装成功
Realize all, race, allsettled and any of the simple version of promise by yourself
111. Network security penetration test - [privilege escalation 9] - [windows 2008 R2 kernel overflow privilege escalation]
Attack and defense world ----- summary of web knowledge points
NGUI-UILabel
千人规模互联网公司研发效能成功之路
Static routing assignment of network reachable and telent connections
30. Feed shot named entity recognition with self describing networks reading notes