当前位置:网站首页>【机器人手眼标定】eye in hand
【机器人手眼标定】eye in hand
2022-07-06 02:00:00 【十年一梦实验室】
/*hand-eye calibration using TSAI method*/
#include <stdlib.h>
#include <iostream>
#include <fstream>
#include <opencv2/core/core.hpp>
#include <opencv2/calib3d/calib3d.hpp>
#include <opencv2/highgui/highgui.hpp>
#include <opencv2/imgproc/imgproc.hpp>
#include <eigen3/Eigen/Core>
#include <eigen3/Eigen/Geometry>
#include <eigen3/Eigen/LU>
#include <eigen3/Eigen/Dense>
#include <eigen3/Eigen/StdVector>
#include <opencv2/core/eigen.hpp>
#define PI 3.1415926
using namespace std;
using namespace cv;
using namespace Eigen;
//https://www.cnblogs.com/long5683/p/10094122.html
int num_of_all_images = 70;//拍摄70次?
// 行列方向内角点数量
cv::Size board_size = cv::Size(9, 7);//9行7列 角点
// 标定板棋盘格实际尺寸(单位要与pose.txt中机器人位置的单位一致) mm
cv::Size2f square_size = cv::Size2f(25, 25);//25x25mm
Eigen::Matrix3d skew(Eigen::Vector3d V);//反对称矩阵。 由向量生成
Eigen::Matrix4d quat2rot(Eigen::Vector3d q);//单位四元数转 旋转矩阵
Eigen::Vector3d rot2quat(Eigen::MatrixXd R);
Eigen::Matrix4d transl(Eigen::Vector3d x);
Eigen::Matrix4d handEye(std::vector<Eigen::Matrix4d, Eigen::aligned_allocator<Eigen::Matrix4d> > bHg,
std::vector<Eigen::Matrix4d, Eigen::aligned_allocator<Eigen::Matrix4d> > cHw);
Eigen::Matrix4d handEye1(std::vector<Eigen::Matrix4d, Eigen::aligned_allocator<Eigen::Matrix4d> > bHg,
std::vector<Eigen::Matrix4d, Eigen::aligned_allocator<Eigen::Matrix4d> > cHw);
int handEye_calib(Eigen::Matrix4d &gHc, std::string path);
// skew - returns skew matrix of a 3x1 vector.
// cross(V,U) = skew(V)*U 叉乘计算
// S = skew(V)
// 0 -Vz Vy
// S = Vz 0 -Vx
// -Vy Vx 0
// See also: cross
Eigen::Matrix3d skew(Eigen::Vector3d V)//反对称矩阵
{
Eigen::Matrix3d S;
S <<
0, -V(2), V(1),
V(2), 0, -V(0),
-V(1), V(0), 0;
return S;
}
// quat2rot - a unit quaternion(3x1) to converts a rotation matrix (3x3)
//单位四元数(3x1)转换旋转矩阵(3x3)
// R = quat2rot(q)
//
// q - 3x1 unit quaternion 单位四元数
// R - 4x4 homogeneous rotation matrix (translation component is zero) 4x4齐次旋转矩阵(平移分部为0)
// q = sin(theta/2) * v 单位四元数:
// theta - rotation angle 旋转角
// v - unit rotation axis, |v| = 1 单位旋转轴
//
// See also: rot2quat, rotx, roty, rotz, transl, rotvec
Eigen::Matrix4d quat2rot(Eigen::Vector3d q)
{
double p = q.transpose()*q;//单位四元数长度
if (p > 1)
std::cout << "Warning: quat2rot: quaternion greater than 1";//确保是单位四元数
double w = sqrt(1 - p); //计算q.w // w = cos(theta/2)
Eigen::Matrix4d R;
R << Eigen::MatrixXd::Identity(4, 4);//初始化齐次单位矩阵
Eigen::Matrix3d res;
res = 2 * (q*q.transpose()) + 2 * w*skew(q);
res = res + Eigen::MatrixXd::Identity(3, 3) - 2 * p*Eigen::MatrixXd::Identity(3, 3);
R.topLeftCorner(3, 3) << res;//替换旋转矩阵
return R;
}
// rot2quat - converts a rotation matrix (3x3) to a unit quaternion(3x1)
//
// q = rot2quat(R)
//
// R - 3x3 rotation matrix, or 4x4 homogeneous matrix
// q - 3x1 unit quaternion
// q = sin(theta/2) * v
// teta - rotation angle
// v - unit rotation axis, |v| = 1
// See also: quat2rot, rotx, roty, rotz, transl, rotvec
Eigen::Vector3d rot2quat(Eigen::MatrixXd R)
{
// can this be imaginary?这可能是想象中的吗?
double w4 = 2 * sqrt(1 + R.topLeftCorner(3, 3).trace());
Eigen::Vector3d q;
q << (R(2, 1) - R(1, 2)) / w4,
(R(0, 2) - R(2, 0)) / w4,
(R(1, 0) - R(0, 1)) / w4;
return q;//单位四元数
}
// TRANSL Translational transform平移变换
//
// T= TRANSL(X, Y, Z)
// T= TRANSL( [X Y Z] )
//
// [X Y Z]' = TRANSL(T)
//
// [X Y Z] = TRANSL(TG)
//
// Returns a homogeneous transformation representing a
// translation of X, Y and Z.
//
// The third form returns the translational part of a
// homogenous transform as a 3-element column vector.
//
// The fourth form returns a matrix of the X, Y and Z elements
// extracted from a Cartesian trajectory matrix TG.
//
// See also ROTX, ROTY, ROTZ, ROTVEC.
// Copyright (C) Peter Corke 1990
Eigen::Matrix4d transl(Eigen::Vector3d x)//齐次形式的3D矢量
{
Eigen::Matrix4d r;
r << Eigen::MatrixXd::Identity(4, 4);
r.topRightCorner(3, 1) << x;
return r;
}
//Eigen内存分配器aligned_allocator
//用每两个 K = (M*M - M) / 2
//参数: gHg:机器人末端位姿向量。 cHw: 图像像素坐标系在相机坐标系下的位姿向量。 输出: 相机在机器人末端坐标系下的位姿矩阵。
Eigen::Matrix4d handEye(std::vector<Eigen::Matrix4d, Eigen::aligned_allocator<Eigen::Matrix4d> > bHg,
std::vector<Eigen::Matrix4d, Eigen::aligned_allocator<Eigen::Matrix4d> > cHw)
{
int M = bHg.size();
// Number of unique camera position pairs唯一相机位置对的数量
int K = (M*M - M) / 2;
// will store: skew(Pgij+Pcij)
Eigen::MatrixXd A;
A = Eigen::MatrixXd::Zero(3 * K, 3);
// will store: Pcij - Pgij
Eigen::MatrixXd B;
B = Eigen::MatrixXd::Zero(3 * K, 1);
int k = 0;
// Now convert from wHc notation to Hc notation used in Tsai paper.现在从 wHc 符号转换为 Tsai 论文中使用的 Hc 符号。
std::vector<Eigen::Matrix4d, Eigen::aligned_allocator<Eigen::Matrix4d> > Hg = bHg;
std::vector<Eigen::Matrix4d, Eigen::aligned_allocator<Eigen::Matrix4d> > Hc = cHw;
for (int i = 0; i < M; i++)
{
for (int j = i + 1; j < M; j++)
{
//Transformation from i-th to j-th gripper pose and the corresponding quaternion从第 i 个到第 j 个夹持器位姿和相应的四元数的转换
Eigen::Matrix4d Hgij = Hg.at(j).lu().solve(Hg.at(i));
Eigen::Vector3d Pgij = 2 * rot2quat(Hgij);
// Transformation from i-th to j-th camera pose and the corresponding quaternion
Eigen::Matrix4d Hcij = Hc.at(j)*Hc.at(i).inverse();
Eigen::Vector3d Pcij = 2 * rot2quat(Hcij);
// Form linear system of equations
k = k + 1;
// left-hand side
A.block(3 * k - 3, 0, 3, 3) << skew(Pgij + Pcij);
// right-hand side
B.block(3 * k - 3, 0, 3, 1) << Pcij - Pgij;
}
}
// Rotation from camera to gripper is obtained from the set of equations:从相机到夹具的旋转是从一组方程获得的:
// skew(Pgij+Pcij) * Pcg_ = Pcij - Pgij
// Gripper with camera is first moved to M different poses, then the gripper
// .. and camera poses are obtained for all poses. The above equation uses
// .. invariances present between each pair of i-th and j-th pose.
// Solve the equation A*Pcg_ = B
Eigen::Vector3d Pcg_ = A.colPivHouseholderQr().solve(B);
// Obtained non-unit quaternin is scaled back to unit value that
// .. designates camera-gripper rotation
Eigen::Vector3d Pcg = 2 * Pcg_ / sqrt(1 + (double)(Pcg_.transpose()*Pcg_));
// Rotation matrix
Eigen::Matrix4d Rcg = quat2rot(Pcg / 2);
// Calculate translational component计算平移分部
k = 0;
for (int i = 0; i < M; i++)
{
for (int j = i + 1; j < M; j++)
{
// Transformation from i-th to j-th gripper pose
Eigen::Matrix4d Hgij = Hg.at(j).lu().solve(Hg.at(i));
// Transformation from i-th to j-th camera pose
Eigen::Matrix4d Hcij = Hc.at(j)*Hc.at(i).inverse();
k = k + 1;
// Form linear system of equations
// left-hand side
A.block(3 * k - 3, 0, 3, 3) << Hgij.topLeftCorner(3, 3) - Eigen::MatrixXd::Identity(3, 3);
// right-hand side
B.block(3 * k - 3, 0, 3, 1) << Rcg.topLeftCorner(3, 3)*Hcij.block(0, 3, 3, 1) - Hgij.block(0, 3, 3, 1);
}
}
Eigen::Vector3d Tcg = A.colPivHouseholderQr().solve(B);
// incorporate translation with rotation
Eigen::Matrix4d gHc = transl(Tcg) * Rcg;
return gHc;
}
//只用相邻两个 K = M-1
//参数: gHg:机器人末端位姿向量。 cHw: 图像像素坐标系在相机坐标系下的位姿向量。 输出: 相机在机器人末端坐标系下的位姿矩阵。
Eigen::Matrix4d handEye1(std::vector<Eigen::Matrix4d, Eigen::aligned_allocator<Eigen::Matrix4d> > bHg,
std::vector<Eigen::Matrix4d, Eigen::aligned_allocator<Eigen::Matrix4d> > cHw)
{
int M = bHg.size();
// Number of unique camera position pairs
int K = M - 1;
// will store: skew(Pgij+Pcij)
Eigen::MatrixXd A;
A = Eigen::MatrixXd::Zero(3 * K, 3);
// will store: Pcij - Pgij
Eigen::MatrixXd B;
B = Eigen::MatrixXd::Zero(3 * K, 1);
int k = 0;
// Now convert from wHc notation to Hc notation used in Tsai paper.
std::vector<Eigen::Matrix4d, Eigen::aligned_allocator<Eigen::Matrix4d> > Hg = bHg;
std::vector<Eigen::Matrix4d, Eigen::aligned_allocator<Eigen::Matrix4d> > Hc = cHw;
for (int i = 0; i < M - 1; i++)
{
//Transformation from i-th to j-th gripper pose and the corresponding quaternion
Eigen::Matrix4d Hgij = Hg.at(i + 1).lu().solve(Hg.at(i));
Eigen::Vector3d Pgij = 2 * rot2quat(Hgij);
// Transformation from i-th to j-th camera pose and the corresponding quaternion
Eigen::Matrix4d Hcij = Hc.at(i + 1)*Hc.at(i).inverse();
Eigen::Vector3d Pcij = 2 * rot2quat(Hcij);
//Form linear system of equations
k = k + 1;
//left-hand side
A.block(3 * k - 3, 0, 3, 3) << skew(Pgij + Pcij);
//right-hand side
B.block(3 * k - 3, 0, 3, 1) << Pcij - Pgij;
}
// Rotation from camera to gripper is obtained from the set of equations:
// skew(Pgij+Pcij) * Pcg_ = Pcij - Pgij
// Gripper with camera is first moved to M different poses, then the gripper
// .. and camera poses are obtained for all poses. The above equation uses
// .. invariances present between each pair of i-th and j-th pose.
// Solve the equation A*Pcg_ = B
Eigen::Vector3d Pcg_ = A.colPivHouseholderQr().solve(B);
// Obtained non-unit quaternin is scaled back to unit value that
// .. designates camera-gripper rotation
Eigen::Vector3d Pcg = 2 * Pcg_ / sqrt(1 + (double)(Pcg_.transpose()*Pcg_));
// Rotation matrix
Eigen::Matrix4d Rcg = quat2rot(Pcg / 2);
// Calculate translational component
k = 0;
for (int i = 0; i < M - 1; i++)
{
// Transformation from i-th to j-th gripper pose
Eigen::Matrix4d Hgij = Hg.at(i + 1).lu().solve(Hg.at(i));
// Transformation from i-th to j-th camera pose
Eigen::Matrix4d Hcij = Hc.at(i + 1)*Hc.at(i).inverse();
// Form linear system of equations
k = k + 1;
// left-hand side
A.block(3 * k - 3, 0, 3, 3) << Hgij.topLeftCorner(3, 3) - Eigen::MatrixXd::Identity(3, 3);
B.block(3 * k - 3, 0, 3, 1) << Rcg.topLeftCorner(3, 3)*Hcij.block(0, 3, 3, 1) - Hgij.block(0, 3, 3, 1);
B.block(3 * k - 3, 0, 3, 1) << Rcg.topLeftCorner(3, 3)*Hcij.block(0, 3, 3, 1) - Hgij.block(0, 3, 3, 1);
}
Eigen::Vector3d Tcg = A.colPivHouseholderQr().solve(B);
// incorporate translation with rotation
Eigen::Matrix4d gHc = transl(Tcg) * Rcg;
return gHc;
}
//参数:标定结果。 数据目录路径
int handEye_calib(Eigen::Matrix4d &gHc, std::string path)
{
ofstream ofs(path + "/output.txt");//文件输出流:标定过程中的日志。以及标定结果 内参和畸变系数。
std::vector<cv::Mat> images;//图片矢量
// 读入图片
std::cout << "******************读入图片......******************" << std::endl;
ofs << "******************读入图片......******************" << std::endl;//输出到文件
for (int i = 0; i < num_of_all_images; i++)//遍历所有图片
{
std::string image_path;
image_path = path + "/" + std::to_string(i) + ".png";//1.png 2.png 图片路径
cv::Mat image = cv::imread(image_path, 0);//读取图片到内存 image
std::cout << "image_path: " << image_path << std::endl;//输出图片路径
if (!image.empty())//图片非空
images.push_back(image);//添加到矢量
else
{
std::cout << "can not find " << image_path << std::endl;//无法找到图片
exit(-1);
}
}
// 更新实际图片数量
int num_of_images = images.size();
std::cout << "******************读入图片完成******************" << std::endl;
ofs << "******************读入图片完成!******************" << std::endl;
std::cout << "实际图片数量: " << num_of_images << std::endl;
ofs << "实际图片数量: " << num_of_images << std::endl;
// 提取角点
std::cout << "******************开始提取角点......******************" << std::endl;
ofs << "******************开始提取角点......******************" << std::endl;
// 图像尺寸
cv::Size image_size;
std::vector<cv::Point2f> image_points_buff;//二维点矢量
std::vector<std::vector<cv::Point2f>> image_points_seq;//图像点集 序列
int num_img_successed_processing = 0;//成功处理的图片数量
for (int i = 0; i < images.size(); i++)//遍历所有图片
{
cv::Mat image = images[i];//取一个图片
if (i == 0)
{
// 第一幅图像
image_size.width = image.cols;//图像宽度:像素
image_size.height = image.rows;//图像高度
}
//9行7列角点, 找出棋格板角点,写入image_points_buff。
/*flags:棋盘格检测角点方法设置标置位
CALIB_CB_ADAPTIVE_THRESH 使用自适应阈值将灰度图像转化为二值图像,而不是固定的由图像的平均亮度计算出来的阈值
CALIB_CB_NORMALIZE_IMAGE 在利用固定阈值或者自适应的阈值进行二值化之前,先使用equalizeHist来均衡化图像gamma值。
CALIB_CB_FILTER_QUADS 使用其他的准则(如轮廓面积,周长,类似方形的形状)来去除在轮廓检测阶段检测到的错误方块。
CALIB_CB_FAST_CHECK 在图像上快速检测一下棋盘格角点,如果没有棋盘格角点被发现,绕过其它费时的函数调用,这可以在图像没有棋盘格被观测以及恶劣情况下缩短整个函数执行时间。*/
if (0 == cv::findChessboardCorners(image, board_size, image_points_buff,
cv::CALIB_CB_ADAPTIVE_THRESH | cv::CALIB_CB_NORMALIZE_IMAGE /*+ cv::CALIB_CB_FAST_CHECK*/))
{
std::cout << "can not find chessboard corners! " << std::endl;
ofs << "can not find chessboard corners! " << std::endl;
continue;
}
else//找到棋盘格角点
{ //在角点检测中精确化角点位置
//参数 image:输入图像。 image_points_buff:输入角点的初始坐标以及精准化后的坐标用于输出
//winSize:搜索窗口边长的一半,例如如果winSize=Size(5,5),则一个大小为:的搜索窗口将被使用。
//zeroZone:搜索区域中间的dead region边长的一半,有时用于避免自相关矩阵的奇异性。如果值设为(-1,-1)则表示没有这个区域。
//criteria:角点精准化迭代过程的终止条件。也就是当迭代次数超过criteria.maxCount,或者角点位置变化小于criteria.epsilon时,停止迭代过程。
cv::cornerSubPix(image, image_points_buff, cv::Size(3, 3), cv::Size(-1, -1),
cv::TermCriteria(CV_TERMCRIT_EPS + CV_TERMCRIT_ITER, 30, 0.1));//提取亚像素角点信息
// 对粗提取的角点精细化
// cv::find4QuadCornerSubpix(image, image_points_buff, cv::Size(5, 5));
// 保存亚像素角点
image_points_seq.push_back(image_points_buff);//角点先添加到序列
std::cout << "successed processing :" << num_img_successed_processing++ << std::endl;
cv::Mat image_color;
cv::cvtColor(image, image_color, CV_GRAY2BGR);//用于将图像从一个颜色空间转换到另一个颜色空间的转换,从灰度空间转换到RGB和BGR颜色空间
cv::drawChessboardCorners(image_color, board_size, image_points_buff, true);//角点绘制
std::stringstream namestream;//字符串流
std::string name;//字符串
namestream << "/" << i << "_corner.png";//构建字符串流
namestream >> name;//赋值给字符粗
cv::imwrite(path + name, image_color);//将绘制有角点的彩色图像存储到 磁盘
}
}
// 根据检测到角点的图像的数量再次更新图像数目
num_of_images = image_points_seq.size();//检测到角点的图像数量
std::cout << "******************提取角点完成!******************" << std::endl;
ofs << "******************提取角点完成!******************" << std::endl;
// 摄像机标定
std::cout << "******************开始进行相机标定......******************" << std::endl;
ofs << "******************开始进行相机标定......******************" << std::endl;
// 保存标定板上的角点的三维坐标
std::vector<std::vector<cv::Point3f>> object_points;
// 内外参
// 内参
cv::Mat camera_matrix = cv::Mat(3, 3, CV_32FC1, cv::Scalar::all(0));//3x3 零矩阵
std::vector<int> point_counts;//点数 矢量
// 畸变系数: k1, k2, p1, p2, k3
cv::Mat dist_coeff = cv::Mat(1, 5, CV_32FC1, cv::Scalar::all(0));//1x5 零矩阵
//平移向量
std::vector<cv::Mat> t_vec;//
//旋转向量
std::vector<cv::Mat> r_vec;
// 初始化标定板上角点的三维坐标
int i, j, k;
for (k = 0; k < num_of_images; k++)//遍历检测到角点的图像
{
//std::cout << "image.NO:" << k << std::endl;
std::vector<cv::Point3f> temp_point_set;
for (i = 0; i < board_size.height; i++)//每一行
{
for (j = 0; j < board_size.width; j++)//每一列
{
cv::Point3f real_point;
real_point.x = j * square_size.width;//理论x点
real_point.y = i * square_size.height;//理论y点
real_point.z = 0;//默认在z平面
// std::cout << "real_point cordinates" << real_point << std::endl;
temp_point_set.push_back(real_point);//理论点集合
}
}
object_points.push_back(temp_point_set);// 图像理论角点坐标 矢量。 (初始化)每一个内角点的世界坐标
}
//初始化每幅图像上的角点数量
for (int i = 0; i < num_of_images; i++)
{
point_counts.push_back(board_size.width*board_size.height);//图像角点数量 矢量
}
// 开始标定
std::cout << "******************开始运行calibrateCamera!******************" << std::endl;
//参数: object_points:所有图像理论角点坐标。 图像坐标系里角点坐标。
//image_points_seq: 所有图像检测到的角点坐标矢量
//image_size:第一幅图像的大小。为图像的像素尺寸大小,在计算相机的内参和畸变矩阵时需要使用到该参数;
//camera_matrix:相机内参矩阵
//dist_coeff: 畸变系数
//r_vec: 旋转矢量: 理论角点到拍摄的角点的变换矩阵的 旋转矢量。
//t_vec:平移矢量
//0:参数flags为标定时所采用的算法.CV_CALIB_USE_INTRINSIC_GUESS:使用该参数时,在cameraMatrix矩阵中应该有fx,fy,u0,v0的估计值。否则的话,将初始化(u0,v0)图像的中心点,使用最小二乘估算出fx,fy。
/*CV_EXPORTS_W double calibrateCamera( InputArrayOfArrays objectPoints,
InputArrayOfArrays imagePoints,
Size imageSize,
CV_OUT InputOutputArray cameraMatrix,
CV_OUT InputOutputArray distCoeffs,
OutputArrayOfArrays rvecs, OutputArrayOfArrays tvecs,
int flags=0, TermCriteria criteria = TermCriteria(
TermCriteria::COUNT+TermCriteria::EPS, 30, DBL_EPSILON) );*/
cv::calibrateCamera(object_points, image_points_seq, image_size, camera_matrix, dist_coeff, r_vec, t_vec, 0);
std::cout << "******************标定完成!******************" << std::endl;
std::cout << camera_matrix << std::endl;
std::cout << dist_coeff << std::endl;
// 评价标定结果
std::cout << "******************开始评定标定结果......******************" << std::endl;
double total_err = 0.0;
double err = 0.0;
//保存重新计算得到的投影点
std::vector<cv::Point2f> image_points2;
std::cout << std::endl << "每幅图像的标定误差: " << std::endl;
for (int i = 0; i < num_of_images; i++)//遍历每张图像
{
std::vector<cv::Point3f> temp_point_set = object_points[i];//图像坐标系理论角点坐标
// 重映射 参数:
//temp_point_set: 图像坐标系中三维角点坐标。
//r_vec[i]:第i张图像的旋转矢量
//t_vec[i]:第i张图像的平移矢量
//camera_matrix:标定后的内参矩阵
//dist_coeff: 标定后的畸变系数。
//image_points2:第i张图像重新计算的投影点。
cv::projectPoints(temp_point_set, r_vec[i], t_vec[i], camera_matrix, dist_coeff, image_points2);
std::vector<cv::Point2f> temp_image_points = image_points_seq[i];//第i张图像检测到的角点坐标
cv::Mat temp_image_points_Mat = cv::Mat(1, temp_image_points.size(), CV_32FC2);
cv::Mat temp_image_points2_Mat = cv::Mat(1, image_points2.size(), CV_32FC2);
for (int j = 0; j < temp_image_points.size(); j++)
{
temp_image_points_Mat.at<cv::Vec2f>(0, j) = cv::Vec2f(temp_image_points[j].x, temp_image_points[j].y);//检测点
temp_image_points2_Mat.at<cv::Vec2f>(0, j) = cv::Vec2f(image_points2[j].x, image_points2[j].y);//投影点
}
err = cv::norm(temp_image_points_Mat, temp_image_points2_Mat, cv::NORM_L2);//两组点集的二范数
total_err += err /= point_counts[i];//所有图像 角点平均误差 的累加。
std::cout << "第" << i + 1 << "幅图像的平均误差: " << err << "像素" << std::endl;
}
std::cout << std::endl << "总体平均误差: " << total_err / num_of_images << "像素" << std::endl;//所有图像平均误差
std::cout << "******************评价完成!******************" << std::endl;
// 输出标定结果
std::cout << "******************标定结果如下:******************" << std::endl;
std::cout << "相机内参:" << std::endl;
std::cout << camera_matrix << std::endl;
std::cout << "畸变系数:" << std::endl;
std::cout << dist_coeff.t() << std::endl;
// 输出到文件
ofs << "******************标定结果如下:******************" << std::endl;
ofs << "相机内参:" << std::endl;
ofs << camera_matrix << std::endl;
ofs << "畸变系数:" << std::endl;
ofs << dist_coeff.t() << std::endl;
//开始手眼 标定
std::cout << "******************开始运行calibrate handEye!******************" << std::endl;
//https://blog.csdn.net/renweiyi1487/article/details/104097576
/*如果STL容器中的元素是Eigen库数据结构,例如这里定义一个vector容器,元素是Matrix4d ,如下所示:
vector<Eigen::Matrix4d>
这个错误也是和上述一样的提示,编译不会出错,只有在运行的时候出错。解决的方法很简单,定义改成下面的方式:
vector<Eigen::Matrix4d,Eigen::aligned_allocator<Eigen::Matrix4d>>;
其实上述的这段代码才是标准的定义容器方法,只是我们一般情况下定义容器的元素都是C++中的类型,所以可以省略,这是因为在C++11标准中,aligned_allocator管理C++中的各种数据类型的内存方法是一样的,可以不需要着重写出来。但是在Eigen管理内存和C++11中的方法是不一样的,所以需要单独强调元素的内存分配和管理。
*/
std::vector<Eigen::Matrix4d, Eigen::aligned_allocator<Eigen::Matrix4d> > bHg;//机器人末端位姿矩阵 矢量
std::vector<Eigen::Matrix4d, Eigen::aligned_allocator<Eigen::Matrix4d> > cHw;//图像的像素坐标系与相机坐标系间的变换矩阵 矢量
std::ifstream ifs;
ifs.open(path + "/pose.txt", std::ios::in);
if (!ifs.is_open())
{
std::cout << "pose file not found" << std::endl;
return -1;
}
else
{
std::cout << "pose file found" << std::endl;//找到机器人末端位姿文件
}
//读取机器人位姿及转化为eigen matrix
for (int i = 0; i < num_of_images; i++)//几幅图像 几个机器人位姿
{
double temp;
Eigen::Vector3d trans_temp;//平移向量
std::cout << "pose[" << i << "]:\n";
for (int j = 0; j < 3; j++)
{
ifs >> temp;//读取平移向量分部 x /y/z
std::cout << temp << " ";
trans_temp(j) = temp;
}
std::vector<double> v(3, 0.0);
ifs >> v[0] >> v[1] >> v[2];//读取 RPY 三个角度 (绕固定坐标系依次旋转: roll:X-V[0] Pitch:Y-V[1] Yaw:Z-V[2])
std::cout << "RPY: " << v[0] << " " << v[1] << " " << v[2] << " " << std::endl;
//计算姿态四元数: RotZ(V[2])*RotY(V[1])*RotX(V[0]) 欧拉角RPY分别代表Roll(滚转角),Pitch(俯仰角),Yaw(偏航角),分别对应绕XYZ轴旋转
Eigen::Quaterniond m = Eigen::AngleAxisd(v[2] / 180 * M_PI, Eigen::Vector3d::UnitZ())
* Eigen::AngleAxisd(v[1] / 180 * M_PI, Eigen::Vector3d::UnitY())\
* Eigen::AngleAxisd(v[0] / 180 * M_PI, Eigen::Vector3d::UnitX());
double w, x, y, z;
x = m.x(); y = m.y(); z = m.z(); w = m.w();
Eigen::Quaterniond rot_temp(w, x, y, z);//临时姿态四元数
Eigen::Matrix4d pose_temp;//位姿矩阵4X4
pose_temp << Eigen::MatrixXd::Identity(4, 4);//单位化
//四元数转旋转矩阵
pose_temp.topLeftCorner(3, 3) << rot_temp.toRotationMatrix();
pose_temp.topRightCorner(3, 1) << trans_temp;
std::cout << "bHg:" << std::endl;
std::cout << pose_temp << "\n" << std::endl;
bHg.push_back(pose_temp);//机器人末端位姿矩阵 矢量
}
ifs.close();
//r_vec和t_vec转化为Eigen matrix
for (int i = 0; i < num_of_images; i++)//遍历 拍摄次数
{
Eigen::Matrix4d pose_temp;
cv::Mat rot_temp;
//罗德里格斯变换,旋转向量转旋转矩阵
cv::Rodrigues(r_vec.at(i), rot_temp);//旋转向量的长度(模)表示绕轴逆时针旋转的角度(弧度)
Eigen::MatrixXd rot_eigen;
Eigen::MatrixXd trans_eigen;
cv::cv2eigen(rot_temp, rot_eigen);//cv::Mat -> Eigen::MatrixXd
cv::cv2eigen(t_vec.at(i), trans_eigen);
pose_temp.topLeftCorner(3, 3) << rot_eigen;
pose_temp.topRightCorner(3, 1) << trans_eigen;
pose_temp(3, 0) = 0;
pose_temp(3, 1) = 0;
pose_temp(3, 2) = 0;
pose_temp(3, 3) = 1;
cHw.push_back(pose_temp);//图像的像素坐标系与相机坐标系间的变换矩阵 矢量
}
Eigen::AngleAxisd v;//角-轴矢量
for (int m = 0; m < bHg.size(); m++)//遍历机器人末端位姿
{//写入文件output.txt
ofs << "num:" << m << std::endl;//第m个机器人位姿
ofs << "bHg" << std::endl;
ofs << bHg.at(m) << std::endl;//第m个机器人末端位姿矩阵
v.fromRotationMatrix((Matrix3d)bHg.at(m).topLeftCorner(3, 3));//机器人末端位姿旋转矩阵对应的 空间轴角矢量
ofs << "axis: " << v.axis().transpose() << std::endl << "angle: " << v.angle() / PI * 180 << std::endl;//写入文件: 空间旋转轴,旋转角度
ofs << "cHw" << std::endl;
ofs << cHw.at(m) << std::endl;//图像像素坐标系到相机坐标系的变换矩阵
v.fromRotationMatrix((Matrix3d)cHw.at(m).topLeftCorner(3, 3));//空间轴角
ofs << "axis: " << v.axis().transpose() << std::endl << "angle: " << v.angle() / PI * 180 << std::endl;
}
gHc = handEye(bHg, cHw);//计算机器人末端到相机的变换矩阵
std::cout << "\n\n\nCalibration Finished: \n" << std::endl;//标定完毕
std::cout << "gHc" << std::endl;
ofs << std::endl << "gHc" << std::endl;
std::cout << gHc << std::endl;
ofs << gHc << std::endl;//相机相对机器人末端的位姿矩阵,写入output.txt
v.fromRotationMatrix((Matrix3d)gHc.topLeftCorner(3, 3));//空间轴角矢量
std::cout << "axis: " << v.axis().transpose() << std::endl << "angle: " << v.angle() / PI * 180 << std::endl;
ofs << "axis: " << v.axis().transpose() << std::endl << "angle: " << v.angle() / PI * 180 << std::endl;
return 0;
}
int main()
{
Eigen::Matrix4d gHc;//camera 相对hand的位姿矩阵。
handEye_calib(gHc, "./data");
return 1;
}
边栏推荐
- Computer graduation design PHP part-time recruitment management system for College Students
- The ECU of 21 Audi q5l 45tfsi brushes is upgraded to master special adjustment, and the horsepower is safely and stably increased to 305 horsepower
- [Clickhouse] Clickhouse based massive data interactive OLAP analysis scenario practice
- NLP第四范式:Prompt概述【Pre-train,Prompt(提示),Predict】【刘鹏飞】
- VIM usage guide
- Thinking about the best practice of dynamics 365 development collaboration
- NLP fourth paradigm: overview of prompt [pre train, prompt, predict] [Liu Pengfei]
- Comments on flowable source code (XXXV) timer activation process definition processor, process instance migration job processor
- Adapter-a technology of adaptive pre training continuous learning
- Alibaba canal usage details (pit draining version)_ MySQL and ES data synchronization
猜你喜欢
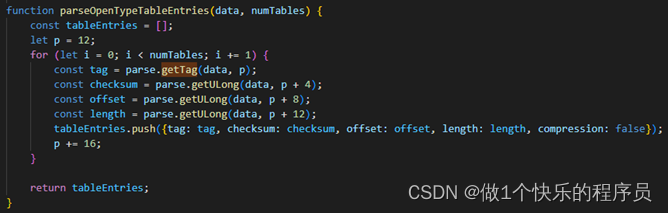
Extracting key information from TrueType font files
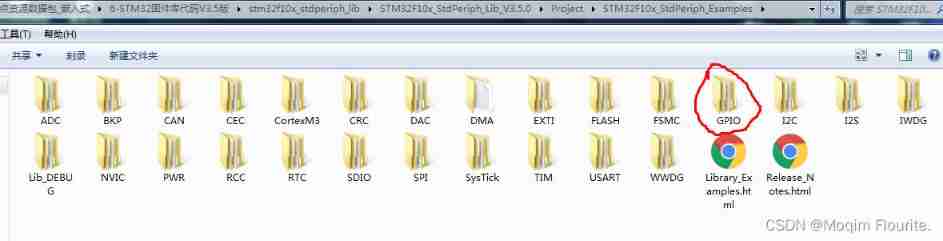
Blue Bridge Cup embedded_ STM32 learning_ Key_ Explain in detail

Adapter-a technology of adaptive pre training continuous learning
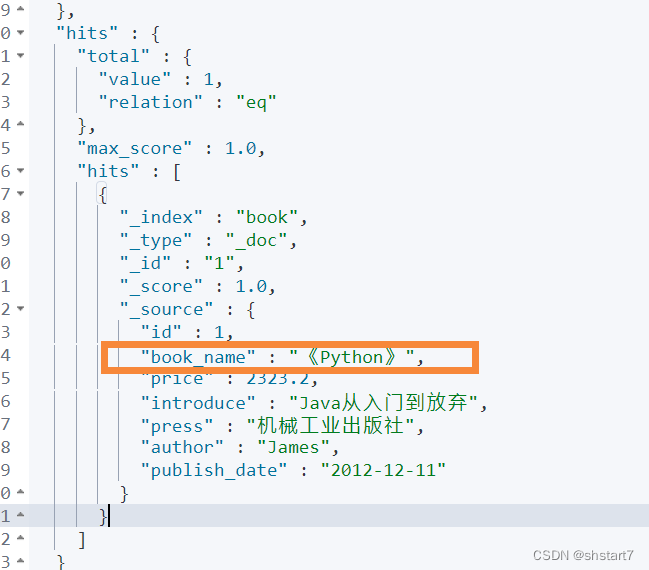
Alibaba canal usage details (pit draining version)_ MySQL and ES data synchronization

NumPy 数组索引 切片
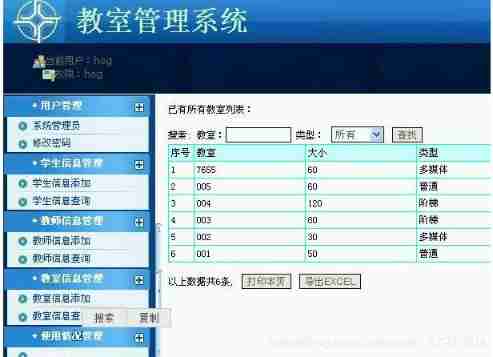
Computer graduation design PHP college classroom application management system

Jisuanke - t2063_ Missile interception

The ECU of 21 Audi q5l 45tfsi brushes is upgraded to master special adjustment, and the horsepower is safely and stably increased to 305 horsepower
Mongodb problem set
Computer graduation design PHP part-time recruitment management system for College Students
随机推荐
[flask] official tutorial -part1: project layout, application settings, definition and database access
Use image components to slide through photo albums and mobile phone photo album pages
Selenium element positioning (2)
Computer graduation design PHP part-time recruitment management system for College Students
Paddle框架:PaddleNLP概述【飞桨自然语言处理开发库】
Redis-Key的操作
Apicloud openframe realizes the transfer and return of parameters to the previous page - basic improvement
You are using pip version 21.1.1; however, version 22.0.3 is available. You should consider upgradin
国家级非遗传承人高清旺《四大美人》皮影数字藏品惊艳亮相!
[flask] obtain request information, redirect and error handling
2022年PMP项目管理考试敏捷知识点(8)
Alibaba canal usage details (pit draining version)_ MySQL and ES data synchronization
Xshell 7 Student Edition
Open source | Ctrip ticket BDD UI testing framework flybirds
leetcode-2.回文判断
Campus second-hand transaction based on wechat applet
[ssrf-01] principle and utilization examples of server-side Request Forgery vulnerability
竞价推广流程
Spark accumulator
Blue Bridge Cup embedded_ STM32 learning_ Key_ Explain in detail