【图的三大存储方式】只会用邻接矩阵就out了

前言：
  在存储图的时候，我们第一时间大多都是想到的是用邻接矩阵，但有时候它不一定能很好地解决我们的问题，我们就要考虑使用其他存储方式。

---

---

一、简述

  对图的操作都需要基于一个存储好的图，图的存储结构必须是一种有序的结构，能够让程序很快定位结点结点 $u$ 和 $v$ 的边($u$，$v$)，我们一般 采用 3 种数据结构存储图：
  邻接矩阵、邻接表和链式向前星

---

二、存储方式

1.邻接矩阵：

邻接矩阵方式的存储基于二维数组的：
 int[][] g = new int[N+1][N+1];
用g[i][j]表示结点 $u$ 到 $v$ 的权值，g[i][j] = INF表示 $i$ 和 $j$之间无边
对于无向图：g[i][j] = g[j][i];
对于有向图：g[i][j] != g[j][i];
举个例子：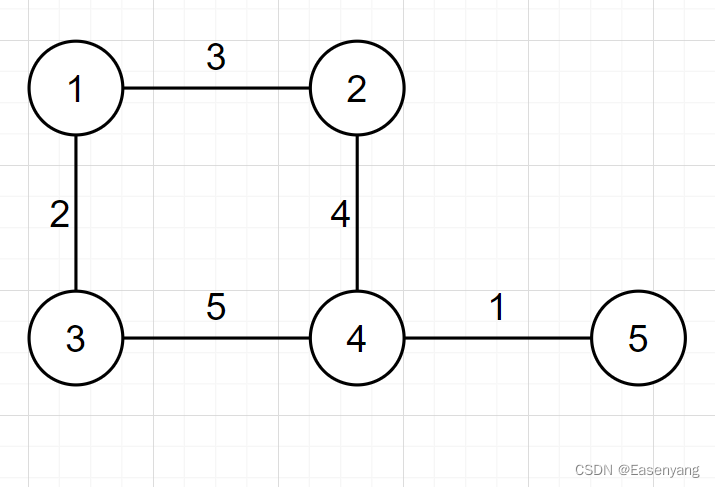

  对于这个图的存储，结点 1 和 2 的权值为 3，就令g[1][2] = g[2][1] = 3,结点 2 和 5 之间无边，就令g[2][5] = g[5][2] = INF。
  常用的做法是初始化所有结点之间的权值都为 INF, 然后根据图去更新各点之间的权值

优点：
  适合稠密图；编码非常简短；对边的存储、查询、更新等操作又快又简单，只需要一步就能访问和修改

缺点：

1. 存储复杂度$O(V^2)$太高。如果用来存储稀疏图，大量的空间会被浪费。例如上面的图，5个结点，10条边（g[ i ][ j ]和g[ j ][ i ]算两条边），但 g[5][5]的空间是25。当图的结点V=10000时，空间为100MB，超过了常见ACM竞赛题的空间限制，一百万个点的图在ACM题种很常见的
2. 一般情况下，不能存储重边。（$u$，$v$）之间可能有两条或者更多的边，它们的权值不同，是不能合并的

2.邻接表

  对于规模大的稀疏图，一般采用邻接表的方式存储。简言之就是存储各个点的邻边，依此方式来实现对图的存储。
  我们可以定义一个edge类来表示边，并定义3个变量from, to, w。分别表示边的起点、终点和权值。

class edge {
    
	int from, to, w;	//边的起点、终点和权值
	public edge(int a, int b, int c) {
    	//构造方法
		this.from = a;
		this.to = b;
		this.w = c;
	}
}

  然后再定义一个集合存储各点的邻边即可。需要注意的是，c++中可以用动态数组vector存储邻边

struct edge{
	int from, to, w;//起点，终点，权值
	edge(int a, int b, int c){
		from=a; to=b; w=c;
	}
};
vector<edge> e[N];//动态数组存放邻边

而Java不能直接创建泛型数组：
ArrayList<edge>[] lists = new ArrayList<edge>[N];这是错误的。我们就可以考虑集合存集合的方式：

	List<List<edge>> list = new ArrayList<>();
	for (int i = 0; i <= N; i++) {
    
		list.add(new ArrayList<>());//先给每个点分配一个空邻边集合
	}

要访问 i 点的邻边，可以通过list.get(i)返回 i 点的邻边集合

举个例子：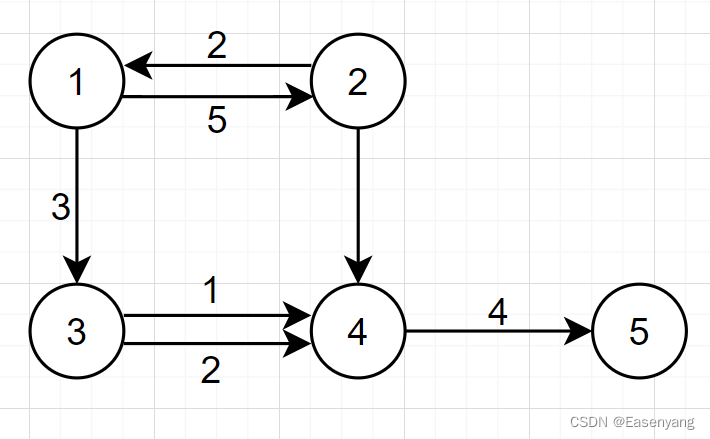

  对于这个图的存储，有重边，但不影响，因为我们操作的是边，结点 3 和 4 的两条边分别new两个edge对象，再加入对应结点的邻边集合即可：

	edge e1 = new  edge(3,4,1);  
	edge e2 = new  edge(3,4,2)
	list.get(3).add(e1); //先获取对应结点的邻边集合，再把邻边放入集合
	list.get(3).add(e2)

其他边的存储同理

优点：
  存储效率高，只需要与边数成正比的空间，存储复杂度为$O(V+E)$，几乎达到了最优的复杂度，而且能存储重边

缺点：
  编程比邻接矩阵麻烦，访问和修改也较慢

3.链式向前星：

  用邻接表存储图非常节省空间，一般的大图也够用了，若空间极其紧张的话，我们就可以考虑更紧凑的存图方式：链式向前星。
  它是对邻接表的改进，不使用集合（或数组）来存放某个点的所有邻边，直接存放一个邻边，然后邻边指向下一个邻边，依次类推。它的实现可以基于几个一维数组。

• 存放各个点的第一个邻边的数组：int[] head = new int[N+1](N是点的数量)
• 存放当前边的下一条邻边的数组：int[] next = new int[M+1](M是边的数量)
• 存放当前边是到哪个点的数组： int[] e = new int[M+1]
• 存放边的权值的数组：     int[] w = new int[M+1]

举个例子：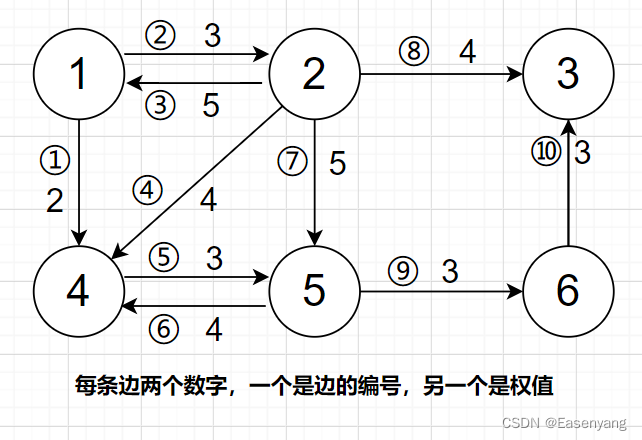

其中各个数组的存储情况如下：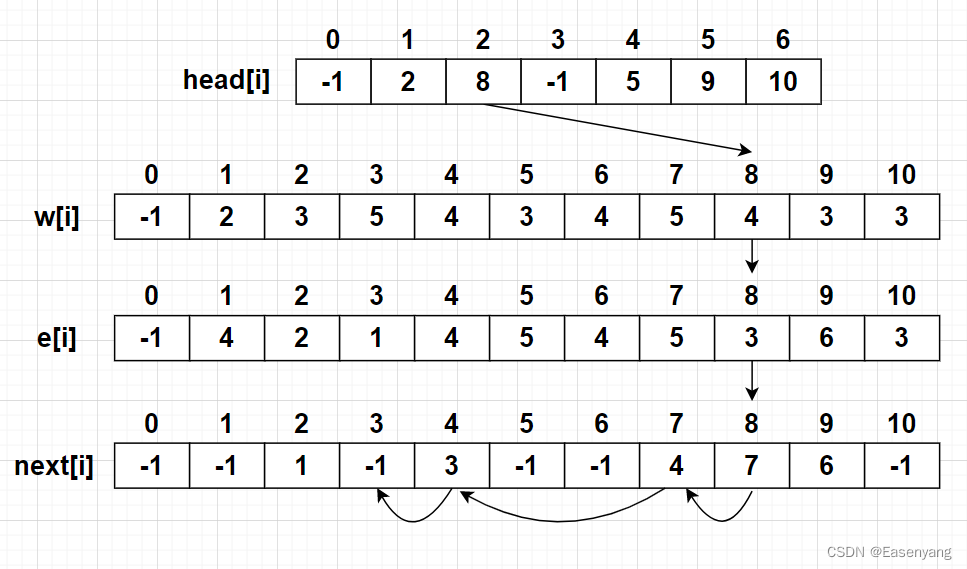

  分析结点 2 的存储，head[2] = 8 表示 2 号结点第一条邻边是 8 号边，e[8] = 3表示 8 号边到的点是 3，next[8] = 7 表示 8 号边的邻边是 7，然后再去找 7 号边的邻边，依此类推，直到某个边没有邻边，即next[i]=-1。最终找到结点 2 的邻边有$（8，7，4，3）$，通过w[8],w[7],w[4],w[3]，就可以找到其邻边的权值
head[i] = -1表示 i 结点没有到其它点的边，即不能到任何点
next[i] = -1表示 i 边不存在下一条邻边了

初始化：

	Arrays.fill(head, -1);	//初始各点第一条邻边为-1
	Arrays.fill(w, -1);		//初始化各边权值为-1
	Arrays.fill(e, -1);		//初始化各边终点为-1
	Arrays.fill(next, -1);	//初始化各边的下一条邻边为-1

存储某条边的代码：

	public static void add(int u, int v, int k) {
    //u是起点，v是终点,k是权值
		//cnt记录当前存储到第几条边了
		w[cnt] = k;	//存储边的权值
		e[cnt] = v;	//置当前边的终点为v
		ne[cnt] = h[u];	//更新当前边的下一个邻边为u点旧的当前邻边
		h[u] = cnt++;	//更新u点的第一个邻边
	}

可以借助结点 2 的head[2] 变化来理解代码：
  head[2]: -1、3、4、7、8，最终指向 8 号边，然后我们可以通过next[8]去找到 7 号邻边，再通过next[7]去找到 4 号邻边， 接着next[4]找到 3 号邻边，next[3] = -1，表示没有邻边了。

再看访问某个点所有邻边的代码：（假设访问结点 2）

for (int j = head[2]; j != -1; j = next[j]) 
	System.out.println(j);	//j就是结点2的一个邻边编号

借助上面的思想就可以找到图的各个元素。这样就实现了图的链式向前星方式的存储

链式向前星与邻接表的存储方式优缺点相同，但是在空间的存储上优于邻接表

---

  因此，针对图问题的不同要求，我们要学会灵活运用对应的存储方式，牢牢掌握这三大存储方式是必要的。
  如果文章对你有帮助，麻烦三连支持一下，谢谢！！！